【JZOJ 省选模拟】tree

图论竞赛题解析

最新推荐文章于 2020-06-07 22:55:53 发布

LK自动机

最新推荐文章于 2020-06-07 22:55:53 发布

阅读量370

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.csdn.net/Eric1561759334/article/details/104874958

本文深入解析了一道图论竞赛题目，通过点分治算法预处理距离矩阵，巧妙地解决了求解特定条件下三元组数量的问题。文章详细阐述了算法思路，包括如何利用递归划分树结构，以及通过计算不满足条件的三元组来间接得出目标答案。

题目

Description
在这里插入图片描述

Input
在这里插入图片描述

Output
一个整数，表示符合要求的三元组的数量。

Sample Input
样例输入：
3 2 11
2 6 2
1 2
2 3

Sample Output
样例输出：
15

Data Constraint
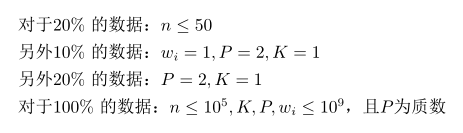
在这里插入图片描述

Hint
在这里插入图片描述

思路

列出 Dist （ u,t） %P，Dist（ t,h） %P，Dist （ u，h） %P 是否等于零的情况
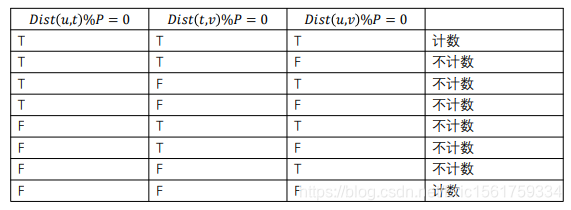
在这里插入图片描述

不难发现不满足要求的都有一对相同，即两对不同。

考虑算出不计数的有多少种

定义dist(u,v)=Dist(u,v)%P==0?0:1

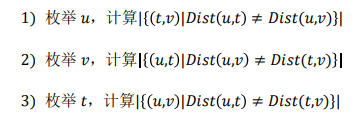
在这里插入图片描述

由于每一种不计数的情况对应上述 3 种情况中的两种，最后要除以2

每一步计算可以用点分治预处理出∀i dist(i,j)=0或1的个数

代码

#include<bits/stdc++.h>
#define fo(i,a,b)for(int i=a,_e=b;i<=_e;++i)
#define fd(i,a,b)for(int i=a,_e=b;i>=_e;--i)
#define ll long long
using namespace std;
const int N=1e5+77;
int n,k,mod,x,y,w[N],in[N],ot[N],all,z,si[N],sz[N],_k[N],aii[N],st[N],en[N],a[N],as,In[N],Ot[N];
bool bz[N];
ll yjy;
vector<int>e[N];
int power(int x,int y)
{
	int t=1;
	for(;y;y>>=1,x=(ll)x*x%mod)if(y&1)t=(ll)t*x%mod;
	return t;
}
void get(int x)
{
	bz[x]=1;si[x]=1;sz[x]=0;
	for(int i:e[x]) if(!bz[i])
		get(i),si[x]+=si[i],sz[x]=max(sz[x],si[i]);
	sz[x]=max(sz[x],all-si[x]);
	bz[x]=0;
	if(sz[x]<sz[z])z=x;
}
void dfs(int x,int fa,int d)
{
	a[++as]=x;
	Ot[x]=((ll)(mod-w[x])*aii[d]+Ot[fa])%mod;
	In[x]=((ll)w[x]*_k[d]+In[fa])%mod;
	bz[x]=1;
	for(int i:e[x])if(!bz[i])
		dfs(i,x,d+1);
	bz[x]=0;
}
void calc(int l,int r,int sgn)
{
	map<int,int>A,B;
	fo(i,l,r) ++A[In[a[i]]],++B[Ot[a[i]]];
	fo(i,l,r)
	{
		int x=a[i];
		ot[x]+=A.count(Ot[x])?A[Ot[x]]*sgn:0;
		in[x]+=B.count(In[x])?B[In[x]]*sgn:0;
	}
}
void fz(int x)
{
	bz[x]=1;
	as=1;a[as]=x;
	Ot[x]=(mod-w[x])%mod;
	In[x]=0;
	for(int i:e[x]) if(!bz[i])
	{
		st[i]=as+1;
		dfs(i,x,1);
		en[i]=as;
		si[i]=en[i]-st[i]+1;
	}
	for(int i:e[x]) if(!bz[i]) calc(st[i],en[i],-1);
	calc(1,as,1);
	for(int i:e[x]) if(!bz[i])
	{
		all=si[i];z=0;
		get(i);fz(z);
	}
}
int main()
{
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	scanf("%d%d%d",&n,&k,&mod);
	k%=mod;
	if(k==0)
	{
		printf("%lld\n",(ll)n*n*n);
		return 0;
	}
	fo(i,1,n) scanf("%d",&w[i]),w[i]%=mod;
	fo(i,2,n)
	{
		scanf("%d%d",&x,&y);
		e[x].push_back(y);
		e[y].push_back(x);
	}
	_k[0]=1;
	fo(i,1,n) _k[i]=(ll)_k[i-1]*k%mod;
	aii[0]=1;aii[1]=power(k,mod-2);
	fo(i,2,n) aii[i]=(ll)aii[i-1]*aii[1]%mod;
	sz[0]=n+1;all=n;get(1);fz(z);
	fo(i,1,n) yjy+=(ll)ot[i]*ot[i]-(ll)in[i]*(n-ot[i])+(ll)(n-in[i])*(n-in[i]);
	printf("%lld\n",yjy);
}