-
思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都要比另一部分的所有数据要小,然后再按此方法对这两部分数据分别进行快排,整个过程可以递归进行,以此达到整个数据变成有序序列。
-
时间复杂度:最优情况O(nlgn) 最差情况O(n2)
-
空间复杂度:O(1)
-
稳定性: 快排是不稳定排序算法
三数取中法(不是快排,是对快排的优化):
由于每次取到的是序列的最右端的元素,取到极值的可能性是很大的,于是我们对他进行优化,每次选序列最左、最右和中间的元素,然后找出其中的中间元素,并把它和最右端的元素相交换,这样的话可以尽量避免取到最值,从而优化快排
代码实现:
// 三数取中法
// 三数取中法是对快排的一个优化,为了避免取到极值,进而导致快排性能变差
int GetMidIndex(int* array, int left, int right)
{
int mid = left + (right - left) / 2;
if (array[left] < array[mid])
{
if (array[mid] < array[right])
{
return mid;
}
else if (array[left] > array[right])
{
return left;
}
else
{
return right;
}
}
else // left > mid
{
if (array[right] > array[left])
{
return left;
}
else if (array[mid] > array[right])
{
return mid;
}
else
{
return right;
}
}
}
快排版本
快排有很多版本,但是最终目的都是为了排序
1.先看提出快排思想的hoare版本


// 分治思想
// [left, right] 左闭右闭区间
void QuickSort(Datatype* array, int left, int right)
{
int mid = 0;
int div = 0;
Datatype key = 0;
int begin = 0;
int end = 0;
// 解释一下这里 left 是有可能大于 right 的 边界细节
// 举个例子 如果此时序列是 1 2 3
// 以3为基准 左边划分没有问题 重点看一下右边
// 递归往右边走的时候 left指向3后面的元素(下标为3的元素)right 指向3(下标为2)
// 那么此时就找不到递归出口(就会Stack overflow)
// 所以这里递归出口的判断条件必须是 ">=" 或者写成 !(left < right)
if (left >= right)
{
return;
}
// 这是我们的一种优化 三数取中法
// 如果每次取序列最优端的那个元素 极易取到极值
// 我们在序列中选择了三个数
// 拿到这三个数的中间值 如果他不是最右边的元素就把他交换到最右边
// 以此来提高快排的性能
mid = GetMidIndex(array, left, right);
if(mid != right)
{
_swap(&array[mid], &array[right]);
}
key = array[right]; // 这是选的基准
begin = left;
end = right;
// begin从前往后找第一个比基准值大的元素
// end从后往前找第一个比基准值小的元素
// 然后交换他们指向的元素 这样小数就在前面 大数就调到后面了
while (begin < end)
{
// begin 找大
while (begin < end && array[begin] <= key)
{
++begin;
}
// end 找小
while (begin < end && array[end] >= key)
{
--end;
}
if (begin < end)
{
_swap(&array[begin], &array[end]);
}
}
// 当begin与end相遇的时候 begin这个位置记录的元素应该是大于基准值的
// 将begin位置元素与序列最右边元素交换
_swap(&array[begin], &array[right]);
// begin记录分割边界 div之前元素都比 div之后的元素小
div = begin;
// 递归排序列的左半部分
QuickSort(array, left, div - 1);
// 递归排序列的右半部分
QuickSort(array, div + 1, right);
}
测试:
void Print(Datatype* array, int size);
void TestQSort()
{
Datatype array[] = { 12, 2, 5, 37, 34, 88, 3, 77, 9, 21, 37 };
int size = sizeof(array) / sizeof(array[0]);
Print(array, size);
QuickSort(array, 0, size-1); // 因为是[left, right]
Print(array, size);
}
int main()
{
TestQSort();
system("pause");
return 0;
}
void Print(Datatype* array, int size)
{
int i = 0;
for (i = 0; i < size; i++)
{
printf("%d ", array[i]);
}
printf("\n");
}
测试结果:
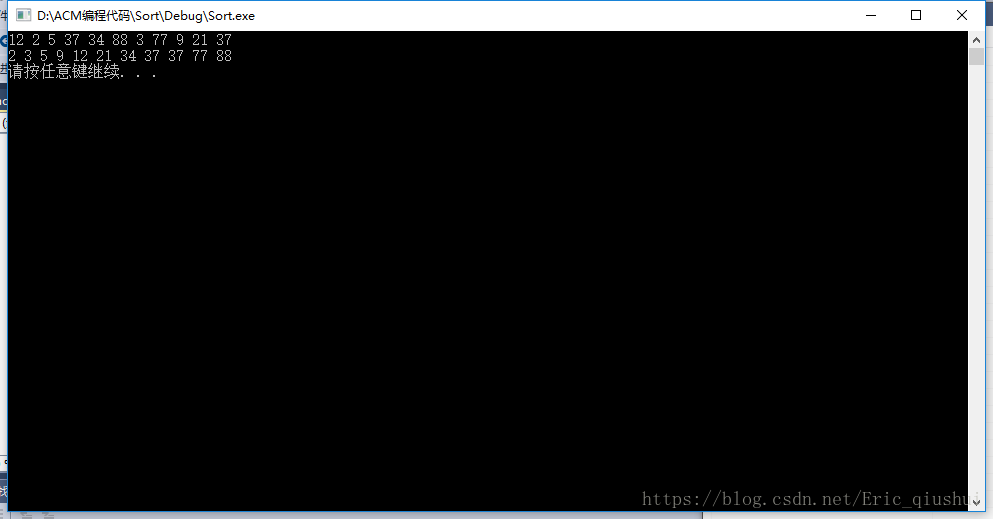
2.挖坑法
这种方法是最容易理解的

// 时间复杂度O(nlgn)
// 空间复杂度O(1)
// 快排
// [ , ) 左闭右开区间
// 挖坑
void QuickSort(Datatype* array, int left, int right)
{
int mid = 0;
int low = left;
int high = right - 1;
Datatype temp = 0;
if (!(left < right)) // 解释一下这里 left 是有可能大于 right 的 边界细节
{ // 举个例子 如果此时序列是 1 2 3
return; // 以3为基准 左边划分没有问题 重点看一下右边
} // 递归往右边走的时候 left指向3后面的元素(下标为3的元素)right 指向3(下标为2)
// 那么此时就找不到递归出口(就会Stack overflow)
// 所以这里递归出口的判断条件必须是 ">=" 或者写成 !(left < right)
mid = GetMidIndex(array, left, right - 1);
if(mid != right - 1)
{
_swap(&array[mid], &array[right - 1]);
}
temp = array[high]; // 这是挖的第一个"坑" 把原来"坑"里的值用temp保存一份 原来的数据不会丢失 覆盖了也没啥事
while (low < high)
{
while (temp >= array[low] && low < high) // 这里有两个陷阱 一是 ">=" 二是 low < high
{
low++;
}
if (low < high)
{
array[high] = array[low]; // 填"坑" 并且low这个位置又是一个新的坑
}
while (temp <= array[high] && low < high)
{
high--;
}
if (low < high)
{
array[low] = array[high]; // 再填"坑"
}
}
array[low] = temp; // 最后把最后一个"坑"填上
QuickSort(array, left, low);
QuickSort(array, low + 1, right);
}
接下来我们来测试一下”挖坑法“版本的快排
void Print(Datatype* array, int size);
void TestQSort()
{
Datatype array[] = { 12, 2, 5, 37, 34, 88, 3, 77, 9, 21, 37 };
int size = sizeof(array) / sizeof(array[0]);
Print(array, size);
QuickSort(array, 0, size-1);
Print(array, size);
}
int main()
{
TestQSort();
system("pause");
return 0;
}
void Print(Datatype* array, int size)
{
int i = 0;
for (i = 0; i < size; i++)
{
printf("%d ", array[i]);
}
printf("\n");
}
测试结果:
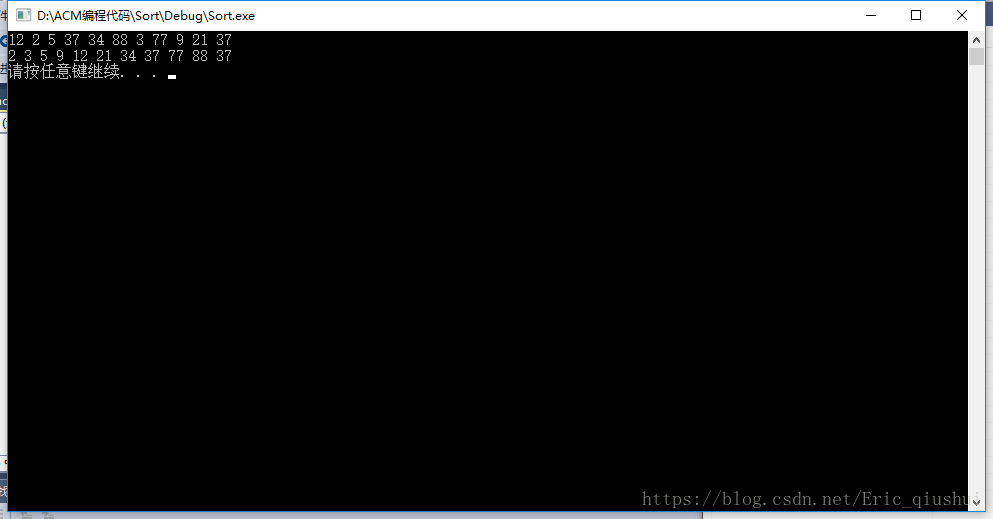
/// 以下为 2019.12.25 修改 👇👇👇 //
由于传错参数,导致最后一个元素没有被排序
修改测试代码:
void Print(Datatype* array, int size);
void TestQSort()
{
Datatype array[] = { 12, 2, 5, 37, 34, 88, 3, 77, 9, 21, 37 };
int size = sizeof(array) / sizeof(array[0]);
Print(array, size);
QuickSort(array, 0, size);
Print(array, size);
}
int main()
{
TestQSort();
system("pause");
return 0;
}
void Print(Datatype* array, int size)
{
int i = 0;
for (i = 0; i < size; i++)
{
printf("%d ", array[i]);
}
printf("\n");
}
测试结果:
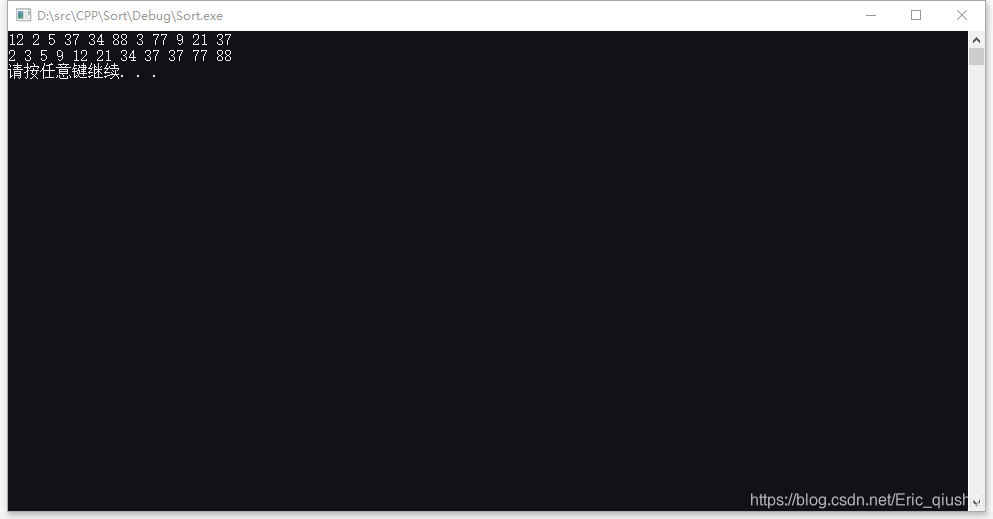
// 以上为 2019.12.25 修改 👆👆👆 //
3.下来我们来介绍一下”前后指针法“
前后两个指针,起始的时候前指针Cur在下标为left位置,后指针Pre在left-1的位置
// 前后指针
// [ , ]
void QuickSort(Datatype* array, int left, int right)
{
int Pre = 0;
int Cur = 0;
Datatype key = 0;
int mid = 0;
int div = 0;
if (!(left < right))
{
return;
}
Pre = left - 1;
Cur = left;
key = array[right];
mid = GetMidIndex(array, left, right);
if(mid != right)
{
_swap(&array[mid], &array[right]);
}
while (Cur < right)
{
if (array[Cur] < key && ++Pre != Cur)
{
_swap(&array[Pre], &array[Cur]);
}
++Cur;
}
_swap(&array[++Pre], &array[right]);
div = Pre;
QuickSort(array, left, div - 1);
QuickSort(array, div + 1, right);
}
测试:
void Print(Datatype* array, int size);
void TestQSort()
{
Datatype array[] = { 12, 2, 5, 37, 34, 88, 3, 77, 9, 21, 37 };
int size = sizeof(array) / sizeof(array[0]);
Print(array, size);
QuickSort(array, 0, size-1);
Print(array, size);
}
int main()
{
TestQSort();
system("pause");
return 0;
}
void Print(Datatype* array, int size)
{
int i = 0;
for (i = 0; i < size; i++)
{
printf("%d ", array[i]);
}
printf("\n");
}
测试结果:
下面第一幅图放错了👇

正确的图是下面这一张👇,程序没有错

本来还想贴完整的程序代码的,可是稍微有点长,我把代码放到GitHub上,需要代码的朋友,去GitHub clone / 查看吧 😃
更多排序请查看我的博客:排序算法或者GitHub:Sort
如有不正,还请指出,有劳!






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








