C++进制转换（整数篇）| 代码大全、方法分析

FHY_patrickpp

已于 2024-07-26 10:07:35 修改

阅读量3.6k

点赞数 50

分类专栏：算法&数据结构文章标签： c++ 算法开发语言

于 2024-07-25 15:28:01 首次发布

本文链接：https://blog.csdn.net/FHY_pp/article/details/140519046

版权

算法&数据结构专栏收录该内容

1 篇文章

订阅专栏

1、前言

制作不易，请多多支持😊！

记得点个赞👍

在漫长的历史发展过程中，中国人发明了“一”到“十”的甲骨文，古印度人发明了“𝟎”到“𝟗”的阿拉伯数字。可是为什么都是十个符号呢?这就要提到一个概念——进制。

2、进制简介

进制也就是进位计数制，是人为定义的带进位的计数方法。对于任何一种进制——X进制，就表示每一位上的数运算时都是逢X进一位。

十进制是逢十进一
十六进制是逢十六进一
二进制就是逢二进一

以此类推，x进制就是逢x进一。
生活中，人们使用十进制计数。十进制计数原理采用“𝟎”~“𝟗”十个符号，运算规则为“逢十进一”，基数是十。类似地，二进制计数原理采用“𝟎”和“𝟏”两个符号，运算规则是“逢二进一”，基数是二。十六进制的基数是十六，用到的符号除了十进制中的"𝟎”~“𝟗”外，还包括英文字母“A”~“F”，分别表示𝟏𝟎~𝟏𝟱，十六进制的运算规则是“逢十六进一”。

3、进制转换

1、X进制转十进制

二进制转十进制：

一个二进制数转换成十进制数的方法是将其表示成“按权展开式”，再按十进
制运算规则求和。如图所示:

说明:这种方法可以扩展到任意n进制。

上代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    string a;
	cin>>a;//输入二进制数
	int ans=0,jz=1,len=a.length();
	for(int i=len-1;i>=0;i--)//核心代码
	{
		ans=ans+(a[i]-48)*jz;
		jz*=2;
	} 
	cout<<ans;//转换完的十进制数
	return 0;
}

十六进制转十进制：

方法同上，在以上代码中添加一个判断一个对字母A~F的特判即可。

代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    string a;
    cin>>a;
    int ans=0,len=a.length(),jz=1;
    for(int i=len-1;i>=0;i--)
	{
		if(a[i]>='0'&&a[i]<='9')//数字
		{
			ans=ans+(a[i]-48)*jz;
			jz*=16;
		}
		else//A~E特判
		{
			ans=ans+(a[i]-55)*jz;
			jz*=16;
		}
	} 
	cout<<ans;
	return 0;
}

注意： 第22行要“-55”，因为'A'的ASCII码=65=55+10，所以，数字10要转换为字符'A'时，就要“-55”

2、十进制转X进制

十进制转二进制：

十进制转二进制可以采用“短除法”,将需要转换的数字不断的进制除𝟐后取余数，直到该数字除尽为止，将所得余数按照逆序输出。因为需要逆序输出，需要有数组来保存的余数。如图：

代码：

#include<bits/stdc++.h>
using namespace std;
int cun[1000002];//存储余数
int main()
{
    int a,i=1;
    cin>>a;
    while(a!=0)//未被除尽时除
    {   
        cun[i]=a%2;//除2取余并存储余数
    	a=a/2;
    	i++;
	}
	for(int x=i-1;x>=1;x--)//倒序输出 
	{
		cout<<cun[x];
	}
	return 0;
}

注意：第十四行要写成“x=i-1”，因为前面while循环里会多加一次i

十进制转十六进制：

方法同上，加上“A”~“F”特判即可。代码：

#include<bits/stdc++.h>
using namespace std;
int cun[1000002];
int main()
{
    int a,i=1;
    cin>>a;
    while(a!=0)
    {   
        cun[i]=a%16;//因为是十六进制，这也要除16
    	a/=16;
    	i++;
	}
	for(int x=i-1;x>=1;x--)
	{
		if(cun[x]<=9)//数字
		{
			cout<<cun[x];
		}
		else//“A”~“F”
		{
			cout<<char(55+cun[x]);
		}
	}
	return 0;
}

3、N进制转M进制

将N进制数转换为M进制数的一个直接的方法就是将N进制数首先转换为十进制数，再从十进制数转换成M进制。这样相当于把十进制当做一个“中转站”来实现N进制到M进制的转换，很大程度上简化了问题。如图：

最难代码:

#include<bits/stdc++.h>
using namespace std;
int ans2[100002];//存储M进制结果
int main()
{
    string a;
    int n,m,ans=0,js=1,t=1;
    cin>>n>>a>>m;/* n:给定数是一个N进制数
                    a:一个合法的N进制数
                    n:需转换成的M进制数 */
    int len=a.length();
	for(int i=len-1;i>=0;i--)//N转十 
	{
		if(a[i]<='9')
		{
			ans=ans+(a[i]-48)*js;
			js*=n; 
		}
		else
		{
			ans=ans+(a[i]-55)*js;
			js*=n;
		}
	}
	while(ans!=0)//十转M
    {   
        ans2[t]=ans%m;
    	ans/=m;
    	t++;
	}
	for(int i=t-1;i>=1;i--)//倒序输出
	{
		if(ans2[i]<10)
		{
			cout<<ans2[i];
		}
		else
		{
			cout<<char(ans2[i]+55);
		}
	}
	return 0;
}

4、特殊转换

二进制与十六进制：

一位二进制数可以有两种状态：“𝟎”和“𝟏”，一位十六进制数有16种状态：“𝟎”~“𝟗”，“A”~“F”。4位二进制组合在一起才能完全表达一位十六进制数，也就是一位十六进制数等同于4位二进制数。
二进制转十六进制方法为:十六进制是取四合一，向左每四位取成一组;组分好以后，对照二进制与十六进制数的对应表，将四位二进制按权相加，得到的数就是一位十六进制数，然后按顺序排列，最后得到的就是十六进制数。如图所示：

将十六进制转为二进制，方法就是一分四，即一个十六进制数分成四个二进制数，用四位二进制按权相加。如图：

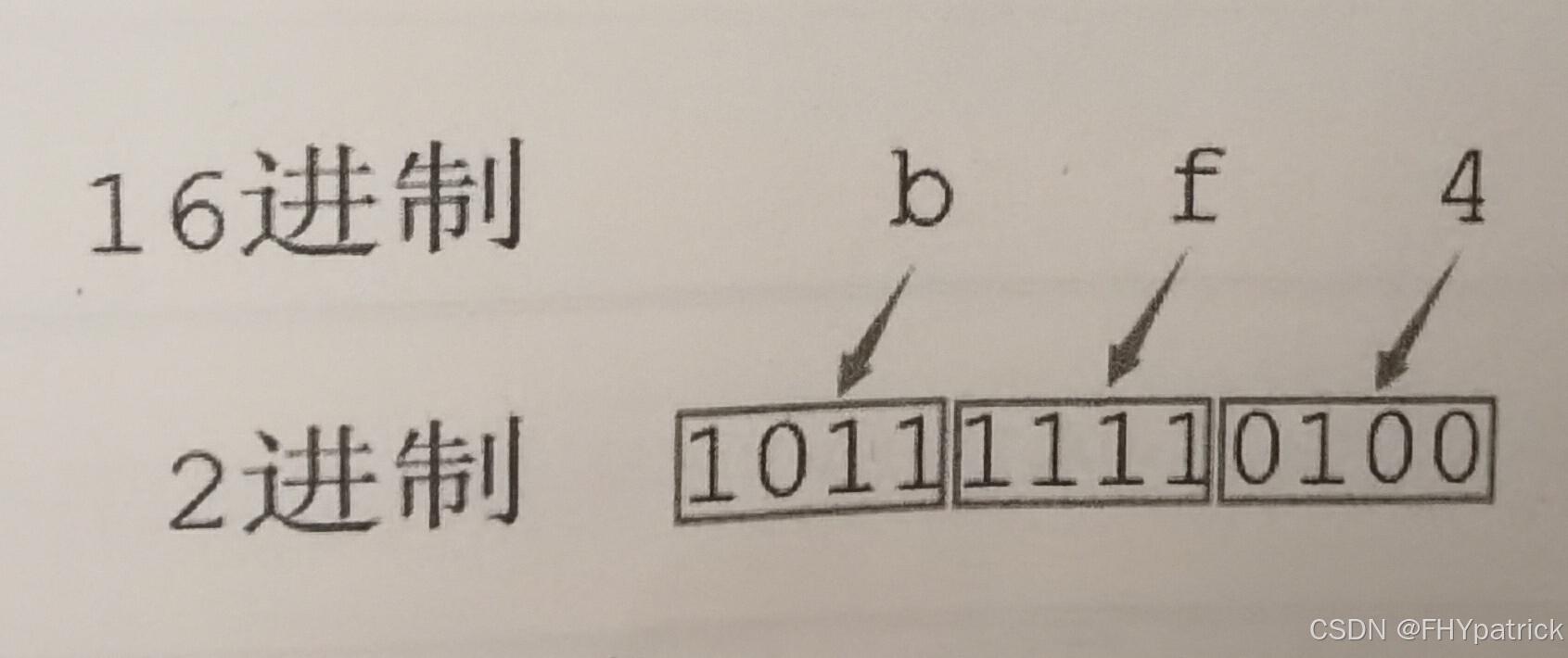
二进制与八进制：

取三合一，从二进制的小数点为分界点，向左每三位取成一位，接着将这三位二进制按权相加，得到的数就是一位八位二进制数，然后，按顺序进行排列，得到的数字就是我们所求的八进制数。如果向左取三位后，取到最高位时候，如果无法凑足三位，可以在最左边，即整数的最高位添0，凑足三位。如图：

5、拓展

系统进制函数：

进制转换除了以上的计算方法，还可以以通过系统函数来解决（不知道OJ能不能AC，不推荐）

示例代码:

#include<bits/stdc++.h>
using namespace std;
int main() 
{
    // 十进制转换为二进制
    int decimal=25;
    string binary=bitset<32>(decimal).to_string();//这一步不精准 
    cout<<"十进制数"<<decimal<<"转换为二进制是"<<binary<<endl;
    // 十进制转换为八进制
    cout<<"十进制数"<<decimal<<"转换为八进制是"<<oct<<decimal<<endl;
    // 十进制转换为十六进制
    cout<<"十进制数"<<decimal<<"转换为十六进制是"<<hex<<decimal<<endl;
    // 二进制转换为十进制
    string bin_str="1101";
    int bin_decimal=stoi(bin_str,nullptr,2);
    cout<<"二进制数"<<bin_str<<"转换为十进制是"<<bin_decimal<<endl;
    return 0;
}

谢谢阅读！