1、递归
当函数用自身来定义时就称为是递归(recursive)的。
递归必须满足四个基本法则:
(1)、基本情形:必须给出基准情况,不用递归就能求出,用于终止递归运算;
(2)、不断推进:对于那些要被递归求解的情形,递归调用必须能够朝着一个基准情形推进;
(3)、设计法则:假设所有的递归调用都能运行;
(4)、合成效益法则:在求解一个问题的同一个实例时,切勿在不同的递归调用中做重复性的工作。
2、迭代
迭代就是利用变量的原值推算出变量的一个新值。
若递归是自己调用自己的话,迭代就是自己不停的调用别人。
3、实例一
求解:阶乘n!之和,即:
示例代码如下:
#include<iostream>
using namespace std;
float fun(int m)
{
float mm=1;
for(int i=1;i<=m;i++) //迭代
{
mm *= i;
}
if(m==0)
return 1; //base case(基准情况)
else
return fun(m-1)+(1/mm); //递归
}
int main()
{
int n;
cout<<"请输入n:";
scanf("%d",&n);
cout<<fun(n)<<endl;;
}4、实例二
求解:有n个台阶,如果一次只能上1个或2个台阶,求一共有多少种上法?
解析:如果只有一级台阶,n=1,很明显只有一种跳法;如果有两级台阶,n=2,则有两种跳法,一种是跳两下1级,一种是直接跳两级;
那么我们来看看如果有n层台阶,可以怎么跳:
n层台阶可以是这么够成的:
(1)、第n层台阶是从第n-1层跳1级上来的
(2)、第n层台阶是从第n-2层直接跳2级上来的
所以可以得到n层的跳法总数是F(n)=F(n-1)+F(n-2)
#include <iostream>
using namespace std;
int Solve(int n)
{
if(n==1)
return 1;
if(n==2)
return 2;
return Solve(n-1)+Solve(n-2);
}
int main()
{
int n;
printf("请输入台阶总数n:");
scanf("%d",&n);
cout<<"共有"<<Solve(n)<<"种跳法"<<endl;
return 0;
}5、实例三
求解:用递归的方法判断一个数组是否为递增数组
基本思想:记录当前最大的,并且判断当前的是否比这个还大,大则继续,否则返回false结束。
#include<iostream>
using namespace std;
bool fun(int a[], int n)
{
if(n==1)
return true;
if(n==2)
return a[n-1]>a[n-2];
return fun(a,n-1) && ( a[n-1]>a[n-2] );
}
int main()
{
int a[]={0,1,2,3,4,5,6,7,8,9};
int n=sizeof(a)/sizeof(int);
cout<<fun(a,n)<<endl;
}








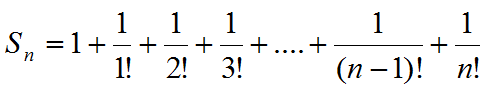














 5469
5469

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








