18日的长春现场赛已经过去4天。虽然说拿到学校的首届银牌还是很值得高兴的,但B题作为这场比赛唯一的数论题,由于时间不够未能AC我实在是感到遗憾。最后半个小时我只推公式推到了sqrt分解log求约数再处理的复杂度,如果再多一点点时间,如果思维再更快点,也许能推出最简化的公式,也许就能6题,就能绝杀金牌。。。可惜没有如果,感觉自己能力还不够,就这样与金牌失之交臂。下午重整了一下大脑,回想起赛场上推题的过程,又花了半个多小时,终于把它做完——虽然题目还没有挂出来等我提交,不过我相信一定是能AC的!——完全的sqrt分解质因数复杂度,不带任何其它包括求约数的log。这样1s跑2W组数据也是能过的吧!
感慨就说这么多——看看这题怎么做。
当然,这种数论题一般就是公式题没错了。那么重点就是——推公式。
先看看f(x)吧。符号打的麻烦,直接手写上图。
然而,如果只推到这里,用约数去算的话,还是会超时的——因为1e9范围内的欧拉函数不可能去打表,还得再用分解质因数方法求。这样的话这题1s是过不去的会TLE。于是利用g(x)的特殊性——公式便可以神奇地继续简化,去掉欧拉函数和求约数!
继续手写上图。
上式中h(n)表示n的约数个数——这显然是分解质因数的过程就可以求出来的。
那么还剩最后一点——n的约数的平方和怎么算。有人肯定会说这个枚举约数就可以了吧!然而我会告诉你这还不够!那么这个还能简化吗?答案当然是肯定的——细细一想,n的约数和我们都知道可以边分解质因数边求,为什么呢?原因很简单,因为约数和是积性函数!!既然这样,为什么平方和就不能是积性函数呢!然后你会发现其实约数的平方和仍然是积性函数。于是这样我们把约数平方和也在分解质因数的过程中求出来了,这样这个题就达到了最简单的复杂度——只有sqrt分解质因数了。约数平方和的公式就不推了,推导过程类似于约数和。在推导过程中你会发现顺便还能推广一下,约数的k次方和也仍然是积性函数!
最后,这道题我就直接给出最后的公式吧!仍然上图。。。
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>
#include <map>
#include <stack>
#include <queue>
#include <set>
using namespace std;
const int MAX = 1e5 + 5;
bool u[MAX];
int prime[MAX], num;
void initial()
{
memset(u, true, sizeof(u));
num = 0;
for(int i = 2; i < MAX; i++)
{
if(u[i])
prime[num++] = i;
for(int j = 0; j < num; j++)
{
if(i*prime[j] >= MAX)
break;
u[i*prime[j]] = false;
if(i%prime[j] == 0)
break;
}
}
}
int n;
void input()
{
scanf("%d", &n);
}
void solve()
{
long long ans = 1, other = n;
for(int i = 0; prime[i]*prime[i] <= n; i++)
{
if(n%prime[i] == 0)
{
int cnt = 1;
long long mul = 1;
while(n%prime[i] == 0)
{
mul *= prime[i];
cnt++;
n /= prime[i];
}
other *= cnt;
mul *= prime[i];
long long a = (mul - 1)/(prime[i] - 1), b = mul + 1, c = prime[i] + 1;
ans *= ((a/c)*(b/c)*c + a%c*(b/c) + b%c*(a/c)); //防溢出计算(mul^2 - 1)/(prime[i]^2 - 1)
}
}
if(n > 1)
{
other *= 2;
ans *= (1 + (long long)n*n);
}
printf("%lld\n", ans - other);
}
int main()
{
initial();
int T;
scanf("%d", &T);
for(int t = 1; t <= T; t++)
{
input();
solve();
}
return 0;
}








 本文回顾了一场比赛中未解决的数论题目,并详细解析了解题思路。通过推导公式简化了计算复杂度,最终实现了高效的求解方法。
本文回顾了一场比赛中未解决的数论题目,并详细解析了解题思路。通过推导公式简化了计算复杂度,最终实现了高效的求解方法。


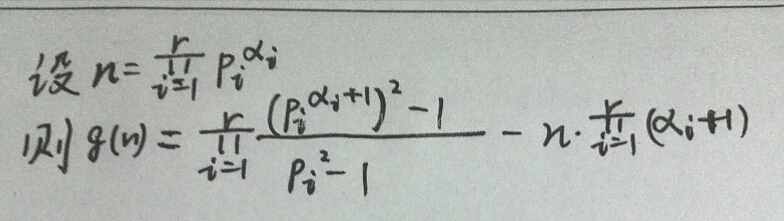

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








