以前做过第三批的题目,今日头条2018校园招聘后端开发工程师(第三批)编程题 - 题解。这一场的题目偏技巧和算法,而第三批的题偏编码。这一场涉及的算法有二分查找、区间动态规划。
原题链接:点这儿。
第一题:用户喜好
题目:
为了不断优化推荐效果,今日头条每天要存储和处理海量数据。假设有这样一种场景:我们对用户按照它们的注册时间先后来标号,对于一类文章,每个用户都有不同的喜好值,我们会想知道某一段时间内注册的用户(标号相连的一批用户)中,有多少用户对这类文章喜好值为 k k 。因为一些特殊的原因,不会出现一个查询的用户区间完全覆盖另一个查询的用户区间(不存在)。
输入:
第1行为
n代表用户的个数 第2行为n个整数,第i个代表用户标号为i的用户对某类文章的喜好度 第3行为一个正整数q代表查询的组数, 第4行到第(3+q)行,每行包含3个整数l,r,k代表一组查询,即标号为l<=i<=r的用户中对这类文章喜好值为k的用户的个数。 数据范围 n<=300000,q<=300000 n <= 300000 , q <= 300000 ,k是整型。
输出:
一共
q行,每行一个整数代表喜好值为k的用户的个数。
样例输入:
5 1 2 3 3 5 3 1 2 1 2 4 5 3 5 3
样例输出:
1 0 2
解析
数据很大,询问300000次,那么每次询问对应的操作的时间复杂度必须是
O(1)
O
(
1
)
或
O(logn)
O
(
l
o
g
n
)
;
这就为我们思考算法提供了方向, O(1) O ( 1 ) 显然是不可能的,那么操作的时间复杂度为 O(logn) O ( l o g n ) 的算法只能是二分查找了,因此,你从这个时间复杂度联想到二分查找,那么这个题你就差不多做出来了;
二分的要求是序列有序,因此不管那么多,先排序,可是按照什么东西来排序呢?由于题目要求在一个时间范围内喜好为k的有多少人,那么可以把相同k值的人放到一起形成一个子序列,然后再根据时间的范围在这个子序列中查找,因此用结构体的二级排序,先按k值的大小升序排序,如果k值相同,再按时间顺序升序排序;
bool sort_cmp(const pair<int, int> &A, const pair<int, int> &B)
{
return A.first == B.first ? A.second < B.second :
A.first < B.first;
}这样的二级排序是稳定排序,故排序后整个序列是k值升序的,各个子序列中的时间也是升序的。
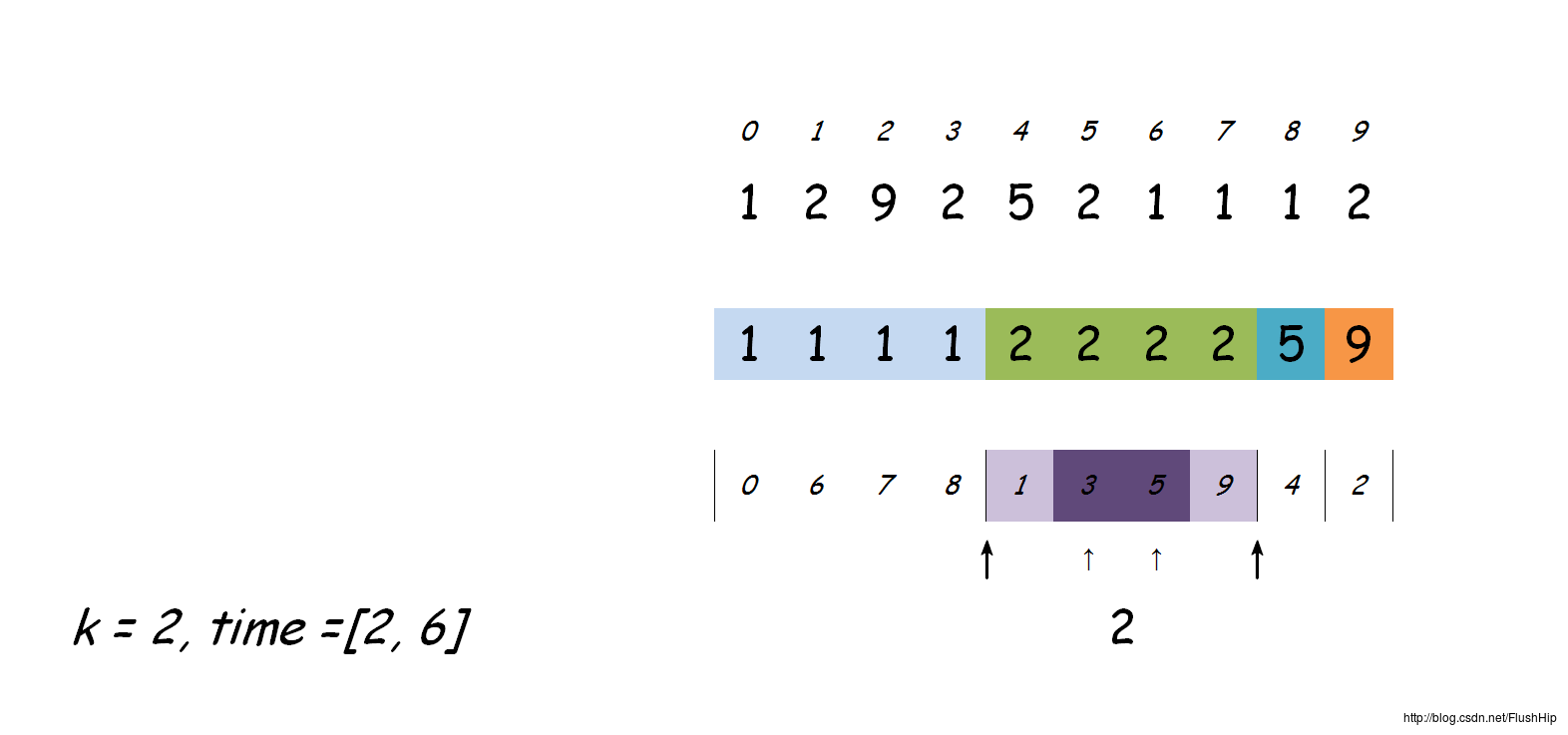
排好序后,就是查找的过程,先用equal_range找到序列中k值为目标k值的子序列,然后用lower_bound与upper_bound在子序列中找到目标时间范围内的最长子序列(用lower_bound找到第一个大于或等于左端点的位置,用upper_bound找到最后一个小于或等于右端点的位置),比如目标时间范围是[3, 7],那么假设最大子序列为[4, 5],
[4,5]⊂[3,7]
[
4
,
5
]
⊂
[
3
,
7
]
,答案就是最长子序列的长度。
如果这个过程还是不清楚,看下图:
equal_range、lower_bound、upper_bound这三个函数的时间复杂度都为
O(logn)
O
(
l
o
g
n
)
,因此问题得到解决。
如果你不熟悉这三个函数,那么你自己可以手写一个求上界的二分,一个求下界的二分,具体可以参考你真的理解二分的写法吗 - 二分写法详解。
代码
#include <bits/stdc++.h>
using namespace std;
bool sort_cmp(const pair<int, int> &A, const pair<int, int> &B)
{
return A.first == B.first ? A.second < B.second :
A.first < B.first;
}
struct find_first_cmp {
bool operator()(const pair<int, int> &P, int k) const
{
return P.first < k;
}
bool operator()(int k, const pair<int, int> &P) const
{
return k < P.first;
}
};
struct find_second_cmp {
bool operator()(const pair<int, int> &P, int k) const
{
return P.second < k;
}
bool operator()(int k, const pair<int, int> &P) const
{
return k < P.second;
}
};
int main()
{
int n, q;
while (EOF != scanf("%d", &n)) {
vector<pair<int, int> > arr;
for (int i = 0, x; i < n; cin >> x, arr.emplace_back(x, ++i)) {}
sort(arr.begin(), arr.end(), sort_cmp);
for (scanf("%d", &q); q--;) {
int L, R, k;
scanf("%d%d%d", &L, &R, &k);
pair<vector<pair<int, int> >::iterator, vector<pair<int, int> >::iterator> sd =
equal_range(arr.begin(), arr.end(), k, find_first_cmp{});
printf("%d\n", upper_bound(sd.first, sd.second, R, find_second_cmp{}) -
lower_bound(sd.first, sd.second, L, find_second_cmp{}));
}
}
return 0;
}
第二题:手串
题目:
作为一个手串艺人,有金主向你订购了一条包含
n个杂色串珠的手串——每个串珠要么无色,要么涂了若干种颜色。为了使手串的色彩看起来不那么单调,金主要求,手串上的任意一种颜色(不包含无色),在任意连续的m个串珠里至多出现一次(注意这里手串是一个环形)。手串上的颜色一共有c种。现在按顺时针序告诉你n个串珠的手串上,每个串珠用所包含的颜色分别有哪些。请你判断该手串上有多少种颜色不符合要求。即询问有多少种颜色在任意连续m个串珠中出现了至少两次。
输入:
第一行输入
n,m,c三个数,用空格隔开。( 1<=n<=10000,1<=m<=1000,1<=c<=50 1 <= n <= 10000 , 1 <= m <= 1000 , 1 <= c <= 50 ) 接下来n行每行的第一个数 numi(0<=numi<=c) n u m i ( 0 <= n u m i <= c ) 表示第i颗珠子有多少种颜色。接下来依次读入 numi n u m i 个数字,每个数字x表示第i颗柱子上包含第x种颜色( 1<=x<=c 1 <= x <= c )
输出:
一个非负整数,表示该手链上有多少种颜色不符需求。
样例输入:
5 2 3 3 1 2 3 0 2 2 3 1 2 1 3
样例输出:
2
解析
暴力枚举大家应该都知道做,先枚举区间起点,然后对区间内的m个珠子逐个检验,时间复杂度为
O(nm)
O
(
n
m
)
达到了
107
10
7
;
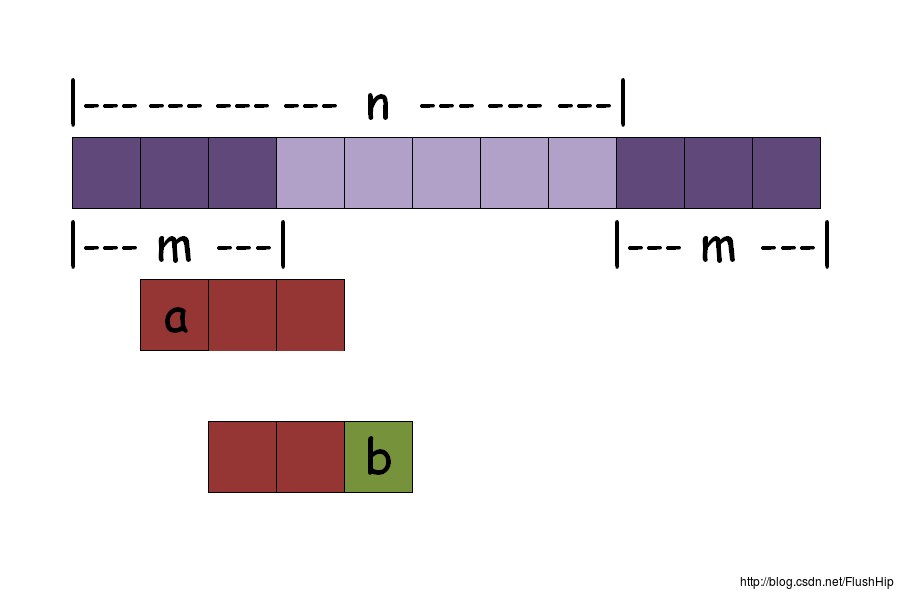
其实对区间内的m个珠子并不需要逐个检验,看下图:
把前面的m个珠子接到序列最后,这样可以保证所有的段都被验证到,这也是化环为序列的一个小技巧;
然后从开头逐段验证,可以发现,图中从第二段到第三段,a消失了,b添加到了序列中,其余的部分不变,因此,不变的这部分在暴力求解中是重复计算了,所以这里要优化,只需要处理下a,b就好了(把a从当前段中删掉,把b加入当前段)就好了。
经过上述优化后,总的时间复杂度变为 O(n) O ( n ) ,这是可以接受的。
代码
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m, c;
while (EOF != scanf("%d%d%d", &n, &m, &c)) {
vector<vector<int> > arr(n + m);
for (int i = 0, num, x; i < n; i++)
for (scanf("%d", &num); num--;
arr[i].push_back((scanf("%d", &x), x))) {}
for (int i = 0; i < m; i++)
arr[n + i] = arr[i];
vector<bool> used(c, false);
map<int, int> color;
for (int i = 0; i < c; color[i++] = 0) {}
for (int i = 0; i < n + m; i++) {
for (int j = 0; !(i < m) && j < (int)arr[i - m].size(); j++)
color[arr[i - m][j] - 1]--;
for (int j = 0; j < (int)arr[i].size(); j++)
color[arr[i][j] - 1]++;
for (map<int, int>::iterator it = color.begin(); it != color.end(); ++it)
used[it->first] = it->second > 1 ? true : used[it->first];
}
int ans = 0;
for (int i = 0; i < c; ans += used[i++]) {}
printf("%d\n", ans);
}
return 0;
}
第三题:字母交换
题目:
字符串
S由小写字母构成,长度为n。定义一种操作,每次都可以挑选字符串中任意的两个相邻字母进行交换。询问在至多交换m次之后,字符串中最多有多少个连续的位置上的字母相同?
输入:
第一行为一个字符串
S与一个非负整数m。 (1<=|S|<=103,1<=m<=106) ( 1 <= | S | <= 10 3 , 1 <= m <= 10 6 )
输出:
一个非负整数,表示操作之后,连续最长的相同字母数量。
样例输入:
abcbaa 2
样例输出:
2
解析
这题算是这场笔试最难的题了,区间动态规划,这也只有一线互联网公司会考,如果是不那么大的厂,顶多考一个背包问题。
要求移动后形成的最长连续子串,这个最长连续子串可能全是a或b……c。因此,这里需要枚举移动后形成的最长连续子串里面所包含的字母;
确定了里面包含的字母,就可以专注于这个字母了,也就是说其余的字母都是没有用的,把它们从序列中挖掉;然后就值剩下目标字母了,目标字母离散地分布在序列中,因此,再离散化一下,搞完之后会生成一个行的序列,之后的动态规划就在新的序列上进行。
下面的图片表达了上述过程:
现在新的序列pos看起来是合在了一起,形成了最长连续子序列,但是,形成这些连续序列所需要的操作次数是多少呢?如果操作次数大于m,那么该序列就是不满足要求的;
因此,这里面就可以得出区间动态规划了,先从小到大枚举段长,依次求得该段长的所有子序列的操作次数,并判断是否小于等于m,如果满足要求,就更新答案。
从小到大枚举段长是为了利用子问题的结果;dp[i][j]表示把pos[i]和pos[j]之间的目标字母移动到一起,形成j - i + 1长度的连续子序列所需要的操作次数;
状态转移方程:dp[i][i + len - 1] = dp[i + 1][i + len - 2] + pos[i + len - 1] - pos[i] - len + 1;,依据是
|x−a|+|x−b|
|
x
−
a
|
+
|
x
−
b
|
在什么时候取得最小值。用最小的移动次数把两个目标字母移动到一起的方法就是把两个目标字母都往中间靠,状态转移方程就是根据这个来的,先把pos[i + 1] ~ pos[i + len - 2]之间的目标字母移动到一起,这个移动次数就是dp[i + 1][i + len - 2],然后把两个端点pos[i]和pos[i + len -1]处的目标字母往中间靠,所需要的移动次数是pos[i + len - 1] - pos[i] - len + 1。
代码
#include <bits/stdc++.h>
using namespace std;
int main()
{
string s;
int m;
while (cin >> s >> m) {
int ans = 1;
for (char c = 'a'; c <= 'z'; c++) {
vector<int> pos;
for (int i = 0; i < (int)s.size(); i++)
if (c == s[i])
pos.push_back(i);
if (pos.size() < 2)
continue;
int ret = 1;
vector<vector<int> > dp(pos.size(), vector<int>(pos.size(), 0));
for (int len = 2; len <= (int)pos.size(); ++len) {
for (int i = 0; i + len - 1 < (int)pos.size(); i++) {
dp[i][i + len - 1] = dp[i + 1][i + len - 2] + pos[i + len - 1] - pos[i] - len + 1;
if (dp[i][i + len - 1] <= m)
ret = len;
}
}
ans = max(ans, ret);
}
cout << ans << endl;
}
return 0;
}

























 456
456

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








