课程设计 霍紫俐

 

 

 

 

 

 

《数据结构课程设计》

 

 

 

 

 

 

课程题目	校园地图
课程编号	j1620102
学生姓名	霍紫俐
所在专业	信息管理与信息技术
所在班级	信管1132
任课老师	易学明
实习时间
设计成绩
老师评语

 

 

 

 

 

 

 

 

一．   问题描述

GDOU是真是一个好地方，校园如一座大花园，美丽而宽广。校园有许多建筑如教学楼、饭堂、宿舍楼、图书馆、体育馆、运动场、商业街、医院等，还有一些著名的风景点。现请根据学校的平面图，找出一些重要的场所，画出学校的平面图（场所可以根据其重要性适当减少），根据实际画出不同点间的路径，并估算每两个场所间的路径长。请设计数据结构并编程，当给出一个出发点和要到达另外一个场所的信息时，请给出最佳路径，并输出路径相关信息。 

 

二．  课程设计要求：

使用数据结构相关知识来做。语言工具不受限。

1、独立完成，设计算法并编写代码，调试通过。

2、写设计说明书。

内容：题目、功能、要求、分析、代码，收获和体会及不足等。

3、以个人独立完成。每一个选择一个题目。选题方式是：自己学号整除5所得的余数是几就做几号题。如学号为12做2号题，学号为5的做0号题。

4、时间：从第13周开始收集资料，进行准备。具体设计时间在16-17周（等实验室安排）。在设计周周五检查（在机房子单独接受老师检查并提问），次周周五前提交设计说明书（实习报告）。

5、实习单独计算成绩，学分1分，成绩好坏和考试没关系。

 

三．  需求分析

1、问题描述

图的最短路径问题是指从指定的某一点v开始，求得从该地点到图中其它各地点的最短路径，并且给出求得的最短路径的长度及途径的地点。除了完成最短路径的求解外，还能对该图进行修改，如顶点以及边的增删、边上权值的修改等。

校园最短路径问题中的数据元素有：

a)     顶点数

b)     边数

c)     边的长度

2、功能需求

    要求完成以下功能：

a)       输出顶点信息：将校园内各位置输出。

b)       输出边的信息：将校园内每两个位置（若两个位置之间有直接路径）的距离输出。

c)       修改：修改两个位置（若两个位置之间有直接路径）的距离，并重新输出每两个位置（若两个位置之间有直接路径）的距离。

d)       求最短路径：输出给定两点之间的最短路径的长度及途径的地点或输出任意一点与其它各点的最短路径。

e)       删除：删除任意一条边。

f)        插入：插入任意一条边。

3、实现要点

   a)  对图的创建采用邻接矩阵的存储结构，而且对图的操作设计成了模板类。为了便于处理，对于图中的每一个顶点和每一条边都设置了初值。

   b)  为了便于访问，用户可以先输出所有的地点和距离。

   c)  用户可以随意修改两点之间好的距离。

   d)  用户可以增加及删除边。

   e)  当用户操作错误时，系统会出现出错提示。

 

四．  概要设计:

1.       抽象数据类型图的定义如下：

ADT Graph{

数据对象V：V是具有相同特性数据元素的集合，称为顶点集。

数据关系R：

R={VR}

VR={（v，w）| v , w∈V, (v , w)表示v和w之间存在路径}

基本操作P：

CreatGraph(&G, V, VR)

初始条件： V是图的顶点集，VR是图中边的集合。

操作结果： 按定义(V, VR) 构造图G。

DestroyGraph(&G)

初始条件： 图G已存在。

操作结果： 销毁图。

LocateVex(G, u) 

初始条件： 图G存在，u和G中顶点具有相同特征。

操作结果： 若G中存在顶点u，则返回该顶点在图中“位置” ；否则返回

其它信息。

GetVex(G, v)

初始条件： 图G存在，v是G中某个顶点。

操作结果： 返回v的信息。

InsertVex(&G, v)

初始条件： 图G存在，v和G中顶点具有相同特征。

操作结果： 在图G中增添新顶点v。

DeleteVex(&G, v)

初始条件： 图G存在，v和G中顶点具有相同特征。

操作结果： 删除G中顶点v及其相关的边。

InsertArc(&G, v, w)

初始条件： 图G存在，v和w是G中两个顶点。

操作结果： 在G中增添弧<v,w>，若G是无向的，则还增添对称弧<w,v>。

DeleteArc(&G, v, w)

初始条件： 图G存在，v和w是G中两个顶点。

操作结果： 在G中删除弧<v,w>，若G是无向的，则还删除对称弧<w,v>。

} ADT Graph

2.       主程序

void main()

{

   初始化；

   while(“命令”!=“退出”)

{

    Switch语句

       接受命令（输入选择项序号）；

      处理命令；

   }

}

3.       本程序运用函数的调用，只有两个模块，它们的调用关系为：

主程序模块

 

带权无向图模块

 

五．  源代码

#include <stdio.h>

#include <iostream.h>

#include<stdlib.h>

#include<conio.h>

#include <malloc.h>

#include<string.h>

#define MAX 10000

#define MAXLEN 8

#define ADJTYPE int

typedef struct                            //图中顶点表示点，存放点名称

{

char name[30];

 int num;

}VEXTYPE;

typedef struct

{

VEXTYPE vexs[MAXLEN];               //顶点的信息

ADJTYPE arcs[MAXLEN][MAXLEN];      //邻接矩阵

int vexnum,arcnum ;                      //顶点数和边数

}MGraph;

MGraph b;

MGraph InitGraph()

{                                      /*建立无向网的邻接矩阵结构*/

int i, j;

MGraph G;

G.vexnum =8;                            //存放顶点数

G.arcnum =13;                           //存放边点数

for(i=0;i<G.vexnum;i++)

G.vexs[i].num=i;

strcpy(G.vexs[0].name,"主教学楼");

strcpy(G.vexs[1].name,"钟海楼");

strcpy(G.vexs[2].name,"图书馆");

strcpy(G.vexs[3].name,"中心广场");

strcpy(G.vexs[4].name,"科技楼");

strcpy(G.vexs[5].name,"体育馆");

strcpy(G.vexs[6].name,"新实验楼");

strcpy(G.vexs[7].name,"行政楼");

for(i=0;i<G.vexnum;i++)

   for(j=0;j<G.vexnum;j++)

      G.arcs[i][j]=MAX;

G.arcs[0][1]=130;

G.arcs[0][2]=80;

G.arcs[0][3]=260;

G.arcs[1][3]=75;

G.arcs[2][4]=50;

G.arcs[3][4]=120;

G.arcs[1][5]=265;

G.arcs[3][5]=85;

G.arcs[3][6]=400;

G.arcs[4][6]=350;

G.arcs[5][6]=120;

G.arcs[4][7]=200;

G.arcs[6][7]=150;

for(i=0;i<G.vexnum;i++)

   for(j=0;j<G.vexnum;j++)

    G.arcs[j][i]=G.arcs[i][j];

return G;

}

void Menu()                               //输出菜单

{

     cout<<endl;

     cout<<endl;

     cout<<endl;

     cout<<"查看校园各地址的信息请按0\n";

     cout<<"查看各地址距离的信息请按1\n";

     cout<<"需要修改请按2\n";

     cout<<"查看最短路径请按3\n";

     cout<<"需要删除某个地址请按4\n";

     cout<<"需要删除某路线请按5\n";

     cout<<"需要插入某路线请按6\n";

     cout<<"需要退出请按7\n";

     cout<<endl;

     cout<<endl;

     cout<<endl;

}

void PutOutVex(MGraph *G)                 //输出每个顶点的信息

{

int v;

for(v=0;v<G->vexnum;v++)

 cout<<G->vexs[v].num<<G->vexs[v].name<<endl;

}

void PutOutArc(MGraph *G)                 //输出每条边的信息

{

for(int i=0;i<G->vexnum;i++)

    for(int j=0;j<G->vexnum;j++)

      if(G->arcs[i][j]<MAX)

   {cout<<"从"<<G->vexs[i].name<<"到"<<G->vexs[j].name<<G->arcs[i][j]<<endl;

    }

}

void Change(MGraph *G)                    //修改

{ int v0,v1,length;

 cout<<"change\n";

  cin>>v0;

  cin>>v1;

 cout<<"length:";

 cin>>length;

 G->arcs[v0][v1]=G->arcs[v1][v0]=length;

}

 

void Dijkstra(MGraph * G)                  //迪杰斯特拉算法求最短路径

{

 intv,w,i,min,t=0,x,v0,v1;

 int final[20],D[20], p[20][20];

 cout<<"请输入起点位置的编号:\n";

 cin>>v0;

 if(v0<0||v0>G->vexnum)

 {

 cout<<"此点编号不存在!请重新输入地址编号:";

  cin>>v0;

 }

 cout<<"请输入终点位置编号:\n";

 cin>>v1;

 if(v1<0||v1>G->vexnum)

 {

 cout<<"此点编号不存在!请重新输入顶点编号:";

  cin>>v1;

 }

 for(v=0;v<G->vexnum;v++)

 {// 初始化final[20],p[20][20],final[v]=1即已经求得v0到v的最短路径，

  //p[v][w]=1则是w从v0到v当前求得最短路径上的顶点，D[v]带权长度

  final[v]=0;

 D[v]=G->arcs[v0][v];

 for(w=0;w<G->vexnum;w++)

   p[v][w]=0;

  if(D[v]<MAX)

  {

  p[v][v0]=1;p[v][v]=1;

  }

 }

 D[v0]=0;final[v0]=1;

 for(i=1;i<G->vexnum;i++)

 {

  min=MAX;

 for(w=0;w<G->vexnum;w++)

  if(!final[w])                                                                                    

   if(D[w]<min){v=w;min=D[w];}

    final[v]=1;

   for(w=0;w<G->vexnum;w++)

    if(!final[w]&&(min+G->arcs[v][w]<D[w]))

     {

     D[w]=min+G->arcs[v][w];

     for(x=0;x<G->vexnum;x++)

      p[w][x]=p[v][x];

      p[w][w]=1;

     }

 }

 cout<<"从"<<G->vexs[v0].name<<"到"<<G->vexs[v1].name<<"的最短路径长度为："<<D[v1]<<endl;

 cout<<"路径为：";

 for(intj=0;j<G->vexnum;j++)

 {

  if(p[v1][j]==1)

  cout<<G->vexs[j].name<<endl;

 }

}

void DeleteVex(MGraph *G)                  //删除某个顶点

{

     int row,col;

     int v0;

     cout<<"请输入要删除的顶点";

     cin>>v0;

     for(inti=v0;i<G->vexnum;i++)

         G->vexs[i]=G->vexs[i+1];

     G->vexnum--;

     for(row=0;row<G->vexnum;row++)

         {

              for(col=v0;col<G->vexnum;col++)

                  G->arcs[row][col]=G->arcs[row][col+1];

         }

     for(col=0;col<G->vexnum;col++)

         {

              for(row=v0;row<G->vexnum;row++)

              G->arcs[col][row]=G->arcs[col][row+1];

         }

}

 

void DeleteArc(MGraph *G)                  //删除某条边

{

 int v0,v1;

 cout<<"请输入两顶点:\n";

 cin>>v0>>v1;

 G->arcs[v0][v1]=MAX;

 G->arcs[v1][v0]=MAX;

}

void InsertArc(MGraph *G)                  //插入某条边

{

 int v0,v1,l=0;

 cout<<"请输入两地址编号:\n";

 cin>>v0>>v1;

 cout<<"请输入路径长度:\n";

 cin>>l;

 G->arcs[v0][v1]=l;

 G->arcs[v1][v0]=l;

}

 

void main()                                //主函数

{ int a;

 b=InitGraph();

 Menu();

 cin>>a;

 while(a!=7)

 {

  switch(a)

  {

  case0:PutOutVex(&b);Menu();break; 

  case1:PutOutArc(&b);Menu();break;

  case2:Change(&b);Menu();break;

  case 3:Dijkstra(&b);Menu();break;

  case4:DeleteVex(&b);Menu();break;   

  case5:DeleteArc(&b);Menu();break;

  case6:InsertArc(&b);Menu();break;

  case7:exit(1);break;

  default:break;

  }

  cin>>a;

 }

}

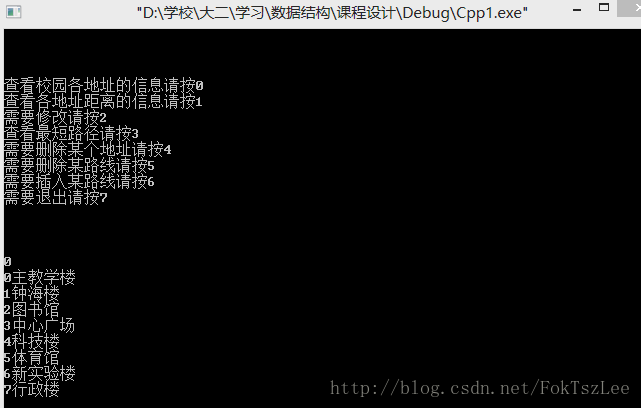
六．    程序运行结果

 

七．    心得

  本次课程设计是我第一次真正把数据结构的知识运用到实际的操作里面，以前很多的时候都是按着书本的程序打上电脑上。因此这次的课程设计我遇到了很多的困难，很多时候因为我对图结构理解还不够深，有很多的地方都不太会，需要身边的同学帮忙协助才能把课程设计勉强的完成了。但是我深知我这样是不足够的，我开始后悔在这个学期里总是只在老师上课时才去学习数据结构，在平时课余的时间里没有利用好csdn老师提供的资料加深学习。只是应付考试而没有真正为了好好利用数据结构而学习数据结构。在本次设计中因为书本的资料不较少，我还在网上寻找了相关的资料查询，