线性回归深入解析-CSDN博客

本文链接：https://blog.csdn.net/Forlogen/article/details/84995783

1. 为什么我们在线性回归中使用的损失函数是平方误差函数？
在线性回归中选用误差平方和作为误差函数，其实就是将误差假定为了0均值的高斯正态分布。这也就是为什么还会存在sigmoid逻辑回归（以伯努利分布分析误差），以及softmax等一般线性回归（以指数分布分析误差）。
假设模型结果与测量值误差满足，均值为0的高斯分布，即正态分布。这个假设是靠谱的，符合一般客观统计规律。如下所示数据x与y的条件概率为：
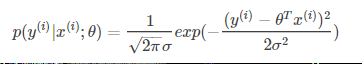
在这里插入图片描述

若使模型与测量数据最接近，即要求其概率积（概率密度函数的连续积）就最大。这样，就形成了一个最大似然函数估计，对最大似然函数估计进行推导，就得出了求导后结果：平方和最小公式。

2. 常见的损失函数有哪些？
0-1损失函数
在这里插入图片描述
平方损失函数

绝对损失函数
在这里插入图片描述
对数损失函数

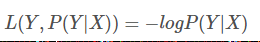
3. 为什么要进行数据的归一化和标准化？
为了在梯度下降计算中，加快梯度下降的速度。标准化后将每个属性的值控制在-1~+1之间，而归一化后将每个特征的尺度控制在相同的范围之内。

4. 如何解决过拟合问题呢？
常见的方法有两种：
• 减少特征的数量，有人工选择，或者采用模型选择算法
• 正则化，即保留所有特征，但降低参数的值的影响。优点：特征很多时，每个特征都会有一个合适的影响因子。
而正则化主要是两种L1正则化和L2正则化，使用L1正则化的回归算法叫Lasso回归，使用L2正则化的回归算法叫Ridge回归。
L1正则化
在这里插入图片描述
L2正则化

5. 在Lasso回归中使用什么方法求解？
如下所示Lasso回归的表达式为
在这里插入图片描述
其中，m为样本个数，n为特征个数。

由于lasso回归的损失函数是不可导的，所以梯度下降算法将不再有效，故利用坐标轴下降法进行求解。坐标轴下降法和梯度下降法具有同样的思想，都是沿着某个方向不断迭代，但是梯度下降法是沿着当前点的负梯度方向进行参数更新，而坐标轴下降法是沿着坐标轴的方向。

坐标轴下降法进行参数更新时，每次总是固定另外n-1个值，求另外一个的局部最优值，这样也避免了Lasso回归的损失函数不可导的问题。坐标轴下降法每轮迭代都需要O(mn)的计算。

数学依据：对于一个可微凸函数，其中为的向量，如果对于一个解，使得在某个坐标轴上都能达到最小值，则就是的全局的最小值点。

6. 最小二乘法怎么解决线性回归问题？

#最小二乘法计算回归系数。xArr为样本数据集，包含m个对象，n种属性。yarr为结果数据集
def standRegres(xArr,yArr):
    xMat = np.mat(xArr)       #转化为x矩阵。自动形成m行n列
    yMat = np.mat(yArr).reshape(len(yArr),1)     #转化为y列向量
    xTx = xMat.T * xMat       #根据文中推导的公示计算回归系数
    if np.linalg.det(xTx) == 0.0:   #对不能求逆的结果返回
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T*yMat)  #最小二乘求导出为0时的权重向量
    return ws

7. 梯度下降法怎么解决线性回归问题？

#梯度下降法计算回归系数。xArr为属性数据集，每行为一个对象。yArr为结果数据集，每行为一个对象的结果。
def gradAscent(xArr,yArr):
    #转换成numpy的矩阵。xMatrix每行为一个对象，每列为一种特征属性
    xMatrix = np.mat(xArr)
    #转换成numpy的矩阵,并变维成列向量                                        
    yMatrix = np.mat(yArr).reshape(len(yArr),1)
    #返回dataMatrix的大小。m为样本对象的个数,n为列数。            
    m, n = np.shape(xMatrix)
    #移动步长,也就是学习速率,控制更新的幅度。                                            
    alpha = 0.001                                                        
    maxCycles = 500
    #初始化权重列向量                                                      
    weights = np.ones((n,1))                                            
    for k in range(maxCycles):
        #梯度上升矢量化公式，计算预测值（列向量）
        h =  xMatrix * weights
        #计算误差                              
        error = h - yMatrix
        # 调整回归系数                                            
        weights = weights - alpha * 2 * xMatrix.T * error                
    return weights.getA()

8. 随机梯度下降法怎么解决线性回归问题？

#随机梯度下降法计算回归系数
def randgradAscent(xArr,yArr):
    #转换成numpy的矩阵。xMatrix每行为一个对象，每列为一种特征属性
    xMatrix = np.mat(xArr)
    #转换成numpy的矩阵,并变维成列向量                                       
    yMatrix = np.mat(yArr).reshape(len(yArr),1)
    #返回dataMatrix的大小。m为样本对象的个数,n为列数。                   
    m, n = np.shape(xMatrix)
    #最大迭代次数                                           
    maxCycles = 100
    #初始化权重列向量                                                     
    weights = np.ones((n,1))                                             
    for i in range(maxCycles):
        for k in range(m):
             # 降低alpha的大小，每次减小1/(j+i)。刚开始的时候可以步长大一点，后面调整越精细
            alpha = 4 / (1.0 + i + k) + 0.01
            #随机梯度上升矢量化公式，计算预测值y                      
            h =  xMatrix[k] * weights
            #计算误差                                      
            error = h - yMatrix[k]
            # 调整回归系数                                            
            weights = weights - 2*alpha * xMatrix[k].T * error                 
    return weights.getA()

9. 数据的中心化处理
在回归问题和一些机器学习算法中，以及训练神经网络的过程中，通常需要对原始数据进行中心化（Zero-centered或者Mean-subtraction）处理和标准化（Standardization或Normalization）处理。
• 目的：通过中心化和标准化处理，得到均值为0，标准差为1的服从标准正态分布的数据。
• 计算过程由下式表示：
在这里插入图片描述
下面解释一下为什么需要使用这些数据预处理步骤。
在一些实际问题中，我们得到的样本数据都是多个维度的，即一个样本是用多个特征来表征的。比如在预测房价的问题中，影响房价的因素有房子面积x1、卧室数量x2等，我们得到的样本数据就是(x1,x2)这样一些样本点，这里的x1，x2又被称为特征。很显然，这些特征的量纲和数值得量级都是不一样的，在预测房价时，如果直接使用原始的数据值，那么他们对房价的影响程度将是不一样的，而通过标准化处理，可以使得不同的特征具有相同的尺度（Scale）。这样，在使用梯度下降法学习参数的时候，不同特征对参数的影响程度就一样了。
简言之，当原始数据不同维度上的特征的尺度（单位）不一致时，需要标准化步骤对数据进行预处理。
下图中以二维数据为例：左图表示的是原始数据；中间的是中心化后的数据，数据被移动大原点周围；右图将中心化后的数据除以标准差，得到为标准化的数据，可以看出每个维度上的尺度是一致的（红色线段的长度表示尺度）。
在这里插入图片描述
其实，在不同的问题中，中心化和标准化有着不同的意义，
• 比如在训练神经网络的过程中，通过将数据标准化，能够加速权重参数的收敛。
• 另外，对于主成分分析（PCA）问题，也需要对数据进行中心化和标准化等预处理步骤。

参考python机器学习案例系列教程——线性函数、线性回归、正则化

10. 早期停止法
在执行梯度下降时，当验证误差达到最小值时停止训练，认为这时的模型的效果是最好的。一般而言，对于随机梯度下降和小批量梯度下降而言，曲线没有这么平滑，所以很难知道是否已经到达了最小值，一种解决八法就是等验证误差超过最小值一段时间后再停止，然后将模型参数回滚到误差最小的位置。

  from sklearn.base import clone
    	sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True, penalty=None,
    	                       learning_rate="constant", eta0=0.0005, random_state=42)
    	
    	minimum_val_error = float("inf")
    	best_epoch = None
    	best_model = None
    	for epoch in range(1000):
    	    sgd_reg.fit(X_train_poly_scaled, y_train)  # continues where it left off
    	    y_val_predict = sgd_reg.predict(X_val_poly_scaled)
    	    val_error = mean_squared_error(y_val, y_val_predict)
    	    if val_error < minimum_val_error:
    	        minimum_val_error = val_error
    	        best_epoch = epoch
    	        best_model = clone(sgd_reg)
    Print (best_epoch, best_model)

11. 弹性网（ElasticNet）
ElasticNet 是一种线性回归模型，它是岭回归和Lasso回归的中间地带，正则化项就是岭回归和Lasso回归的正则项的混合。这种组合允许学习一个稀疏模型，其中很少的权重是非零的，如 Lasso ；同时仍然保持 Ridge 的正则化属性，我们使用 ρ 参数控制 L1 和 L2 的凸组合。

它的成本函数是：
在这里插入图片描述
那么如何选择常用的这三种线性回归模型呢？一般来说，应该避免使用纯线性回归，岭回归往往可以有不错的效果。但当你实际使用的特征只有那么几个时，就更倾向于使用Lasso回归和弹性网，因为他们会将无用特征的权重降为零，其中弹性网的效果一般又会好于Lasso回归。

12. 如果运行的时间足够的长，是否所有的梯度下降方法得到的模型会是一样的？
如果我们的问题都是凸优化问题，而且学习率设置的不是很大，那么所有的梯度下降算法都可以接近全局最优，最终生成的模型非常相似。但是除非逐渐地降低学习率，否则随机梯度下降和小批量梯度下降都不会真正的收敛，他们会在全局最优值附近不断地波动。所以说说，批量梯度下降经过足够长的时间训练可以真正收敛，而随机梯度下降和小批量梯度下降将围绕最小值上下波动。

线性回归问题回顾