P2862 [USACO06JAN]Corral the Cows G

题目链接

Acwing 121. 赶牛入圈
NHFLS Online Judge 1414
luoguP2862

题目

农夫约翰希望为他的奶牛们建立一个畜栏。
这些挑剔的畜生要求畜栏必须是正方形的，而且至少要包含 $C$ 单位的三叶草，来当做它们的下午茶。
畜栏的边缘必须与 $X$，$Y$ 轴平行。
约翰的土地里一共包含 $N$ 单位的三叶草，每单位三叶草位于一个 $1\times 1$ 的土地区域内，区域位置由其左下角坐标表示，并且区域左下角的 X,Y 坐标都为整数，范围在 $1$ 到 $10000$ 以内。
多个单位的三叶草可能会位于同一个 $1\times 1$ 的区域内，因为这个原因，在接下来的输入中，同一个区域坐标可能出现多次。
只有一个区域完全位于修好的畜栏之中，才认为这个区域内的三叶草在畜栏之中。
请你帮约翰计算一下，能包含至少 $C$ 单位面积三叶草的情况下，畜栏的最小边长是多少。

输入格式

第一行输入两个整数 $C$ 和 $N$。
接下来 $N$ 行，每行输入两个整数 $X$ 和 $Y$，代表三叶草所在的区域的 $X,Y$ 坐标。
同一行数据用空格隔开。

输出格式

输出一个整数，代表畜栏的最小边长。

数据范围

$1\le C\le 500,C\le N\le 500$

输入样例：
3 4
1 2
2 1
4 1
5 2
输出样例：
4

题意

有一些三叶草在坐标轴上的整数坐标上，约翰想在其中框选一个正方形的蓄栏，使所框选的区域中三叶草数量大于等于$C$
在所有的合法框选的方案中，求最短的蓄栏的边长
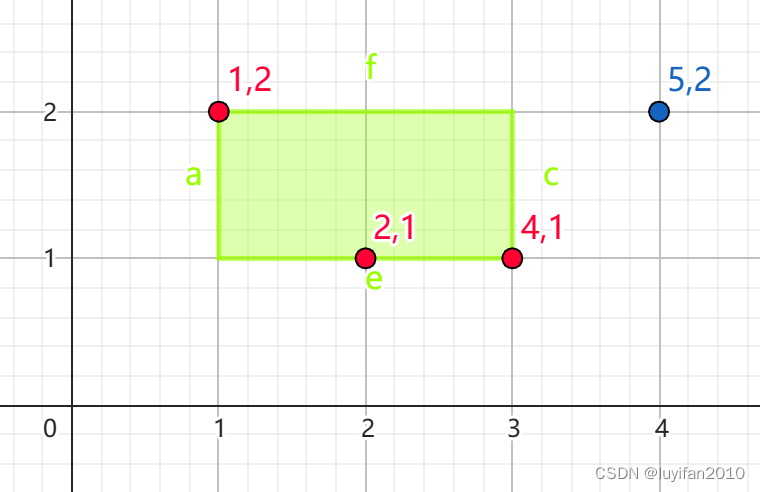
如图所示，为样例数据所展示的土地状况
红色点为框选中的三叶草，蓝点为没被框选中的三叶草，绿框为所围的正方形蓄栏

思路

暴力40分

建立一个二维前缀和数组，$sum[i][j]$代表从$(1,1)$到$(i,j)$有多少堆三叶草
然后我们可以用双重循环枚举左下端点，再用一重循环枚举蓄栏的边长，每次都用二维前缀和计算一下枚举的蓄栏内三叶草的个数，更新答案

二维前缀和
$sum[a][b]=sum[a][b]-sum[i-1][b]-sum[a][j-1]+sum[i-1][j-1]$
$a,b$为右上端点的坐标，$i,j$为左下端点的坐标

时间复杂度为$O(10000^3)>10^8$

#include<bits/stdc++.h>
using namespace std;
#define int long long
int c,n,xma=-0x7fffffff,yma=-0x7fffffff,ans=0x7fffffff,a,b,tmp,x,y; 
short sum[7005][7005];
signed main(){
	scanf("%lld%lld",&c,&n);
	for(int i=1;i<=n;i++)
		scanf("%lld%lld",&x,&y),sum[x][y]++,xma=max(xma,x),yma=max(yma,y);
	for(int i=1;i<=max(xma,yma);i++)
		for(int j=1;j<=max(xma,yma);j++)
			sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+sum[i][j];
			//二维前缀和
	for(int i=1;i<=max(xma,yma);i++)//枚举左下端点x轴
		for(int j=1;j<=max(xma,yma);j++)//枚举左下端点y轴 
			for(int k=1;i+k-1<=max(xma,yma)&&j+k-1<=max(xma,yma);k++){//枚举蓄栏边长 
				a=i+k-1,b=j+k-1;//计算右上端点 
				tmp=sum[a][b]-sum[i-1][b]-sum[a][j-1]+sum[i-1][j-1];
				//计算蓄栏内的三叶草个数 
				if(tmp>=c)ans=min(ans,k);//更新答案 
			}
	printf("%lld",ans);
	return 0;
}

纯离散化80分

看一下数据，$x$和$y$都到$10000$了，空间和时间都肯定爆炸了
但是$n$只有$500$，这说明在$10000^2$的土地中，最多只有$500$个三叶草，其中有很多的空间被浪费了
所以我们可以使用离散化，将三叶草的$x,y$轴分别离散化
对离散化后的$x,y$轴进行二维前缀和
接着开始枚举离散化后的 矩形 ，这里的矩形相当于暴力时的正方形

为什么离散化后要枚举矩形，而不是枚举正方形呢
因为离散化后看似相邻的两个点，可能都隔了十万八千里
我们再用样例来解释
下图为离散化后的土地状况（点上为离散化前的坐标，红色点为框选中的三叶草，蓝点为没被框选中的三叶草，绿框为所围的正方形蓄栏）
可以看到下面两个紧挨着的三叶草在离散化前是不相邻的，如果枚举正方形的话可能会多枚举到其他的点，会让答案错误

根据上面的思路，我们可以写出这个80分的代码
时间复杂度为$O(n^4)=O(500^4)>10^8$

#include<bits/stdc++.h>
using namespace std;
#define int long long
int ans=0x7fffffff,c,n,a,b,len1,len2,sum;
int rankx[505],ranky[505],qzh[505][505],numberx[505],numbery[505];
struct Point{
	int x,y;
}point[505];
signed main(){
	scanf("%lld%lld",&c,&n);
	for(int i=1;i<=n;i++)scanf("%lld%lld",&point[i].x,&point[i].y),rankx[i]=point[i].x,ranky[i]=point[i].y;
	sort(rankx+1,rankx+1+n);//x轴离散化排序 
	sort(ranky+1,ranky+1+n);//y轴离散化排序
	len1=unique(rankx+1,rankx+1+n)-(rankx+1);//x轴离散化去重
	len2=unique(ranky+1,ranky+1+n)-(ranky+1);//y轴离散化去重 
	for(int i=1;i<=n;i++){
		numberx[i]=lower_bound(rankx+1,rankx+1+len1,point[i].x)-rankx;//x轴离散化映射数组
		numbery[i]=lower_bound(ranky+1,ranky+1+len2,point[i].y)-ranky;//y轴离散化映射数组 
		qzh[numberx[i]][numbery[i]]++;//二维前缀和初始化 
	}
	for(int i=1;i<=max(len1,len2);i++)
		for(int j=1;j<=max(len1,len2);j++)
			qzh[i][j]=qzh[i][j]+qzh[i-1][j]+qzh[i][j-1]-qzh[i-1][j-1];
			//二维前缀和
	for(int i=1;i<=max(len1,len2);i++)//枚举左下端点x轴
		for(int j=1;j<=max(len1,len2);j++)//枚举左下端点y轴
			for(int p=i;p<=max(len1,len2);p++)//枚举右上端点x轴
				for(int q=j;q<=max(len1,len2);q++){//枚举右上端点y轴
					sum=qzh[p][q]-qzh[i-1][q]-qzh[p][j-1]+qzh[i-1][j-1];//计算蓄栏内三叶草个数 
					if(sum>=c)ans=min(ans,max(rankx[p]-rankx[i]+1,ranky[q]-ranky[j]+1));//更新答案 
				}
	printf("%lld",ans);
	return 0;
}

离散化+二分答案 100分

看到问题求最小边长时就应该想到用二分答案了，毕竟这是万能优化
用二分答案枚举边长，$check$函数判断当前边长是否可以围出大于等于$c$个三叶草
那$check$函数怎么写呢，由于$x,y$最大为$10000$，所以肯定不能枚举实际坐标，要转而枚举离散化后的**矩形**
由于得到了蓄栏的边长，我们可以枚举右上端点，用$while$循环（收缩）找到第一个也是最小左下端点，这样就可以得到一个框选的矩形了

$rankx[x2]-rankx[x1]+1>mid$
$ranky[y2]-ranky[y1]+1>mid$
$x1,y1$为左下端点，$x2,y2$为右上端点

枚举完$x2,y2$，并收缩得出$x1,y1$后，计算所框选矩形内的三叶草个数，如果达到期望$c$，就可以返回$true$，如果枚举完所有右上端点后，都无法得到足够的三叶草，就返回$false$

#include<bits/stdc++.h>
using namespace std;
#define int long long
int ans=0x7ffffff,c,n,a,b,len1,len2,sum;
int rankx[505],ranky[505],qzh[505][505],numberx[505],numbery[505];
struct Point{
	int x,y;
}point[505];
bool check(int mid){//check函数 
	for(int x1=1,x2=1;x2<=len1;x2++){//x1为左下端点的x轴，x2为右上端点的y轴 
		while(rankx[x2]-rankx[x1]+1>mid)x1++;
		//枚举x2，收缩x1，收缩原因：因为每一个三叶草离散化后，其对应的原始坐标并没有连续，所以要通过收缩来降低时间复杂度 
		for(int y1=1,y2=1;y2<=len2;y2++){
			while(ranky[y2]-ranky[y1]+1>mid)y1++;
			//枚举y2，收缩y1，理由同上 
			sum=qzh[x2][y2]-qzh[x2][y1-1]-qzh[x1-1][y2]+qzh[x1-1][y1-1];//计算出选取矩形中的三叶草个数 
			if(sum>=c)return true;//如果达标，返回true 
		}
	}
	return false;
	//当前蓄栏的边长太短，所围的三叶草个数不够 
}
signed main(){
	scanf("%lld%lld",&c,&n);
	for(int i=1;i<=n;i++)scanf("%lld%lld",&point[i].x,&point[i].y),rankx[i]=point[i].x,ranky[i]=point[i].y;
	sort(rankx+1,rankx+1+n);//离散化排序 
	sort(ranky+1,ranky+1+n);//离散化排序 
	len1=unique(rankx+1,rankx+1+n)-(rankx+1);//离散化去重
	len2=unique(ranky+1,ranky+1+n)-(ranky+1);//离散化去重 
	for(int i=1;i<=n;i++){
		numberx[i]=lower_bound(rankx+1,rankx+1+len1,point[i].x)-rankx;//离散化映射 
		numbery[i]=lower_bound(ranky+1,ranky+1+len2,point[i].y)-ranky;//离散化映射
		qzh[numberx[i]][numbery[i]]++;//二维前缀和初始化 
	}
	for(int i=1;i<=max(len1,len2);i++)
		for(int j=1;j<=max(len1,len2);j++)
			qzh[i][j]=qzh[i][j]+qzh[i-1][j]+qzh[i][j-1]-qzh[i-1][j-1];
			//二维前缀和累加 
	int l=0,r=10001,mid;
	while(l+1<r){//二分答案 
		mid=l+r>>1;
		if(check(mid))r=mid;
		else l=mid;
	}
	printf("%lld",r);
	return 0;
}

总结

离散化oi-wiki
离散化baidu
二分答案是一种很实用的时间优化方式，如果在题目中出现“最小”“最多”“最短”“最长”等表绝对的词语，可以选择去思考一下二分答案的可行性
注意：二分答案的时间复杂度为$O(二分的时间\times check函数的时间)$