[数据结构]二叉查找树-基础版

额

基础信息：（摘自某度百科）
二叉排序树的查找过程和次优二叉树类似，通常采取二叉链表作为二叉排序树的存储结构。中序遍历二叉排序树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉排序树变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。搜索,插入,删除的复杂度等于树高，O(log(n)).

---

废话这么多。

---

逻辑结构

一棵二叉查找树满足一下几条性质。

对于任意节点：
1、其左子节点的键值小于其自身键值
2、其右子节点的键值大于其自身键值
3、任意节点可以代表一棵二叉查找树

如图即是一棵简单的bst(binary search tree):

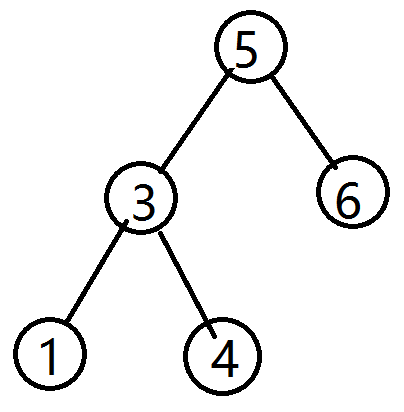
根据其性质，我们又能总结出：

一棵bst的左节点的左节点的左节点。。。的左节点（最左节点）带有这棵树中的最小键值
同理，最右节点带有最大键值
一棵树中不允许带有两个相同键值的节点同时存在

由于数组过于占用空间，我打算用指针实现。
首先声明一个节点结构体。一个节点包括:

指向左子节点与右子节点的指针
键值
(可选)查询值

struct node{
    node *lchild,rchild;
    int key,value;
    node (int k,int v){key=k,val=v;}
    node(){}
};

现在我们来构建一棵树。
根据性质：任意节点可代表一棵二叉查找树，我们要实例化一个根节点。

class BST{
    node *root;
public:
};

一个数据结构所具有的基本素养（划掉）操作包括插入和查询操作。于是我们在BST类中添加如下insert()与query()。

class BST{
    node *root;
public:
    void insert(int key,int val);
    int query(int key);
};

---

具体实现

插入
1、递归版
递归查询的优点是代码量短，但对于刚刚接触递归的童鞋较难理解。
接下来的代码我将逐句解释。

void insert(node &*target,int key,int val){
//一定要注意取址符！！！！！
    if(!target){
        target=new node(key,val);
        return;//递归终止条件，如果当前节点为空，则创建一个新的节点
    }
    //只有对非空节点的访问能够执行到这里
    if(key>target->key)
        insert(target->rchild,key,val);
        //由于待插入键值大于当前结点，所以应该向右子节点插入
    else if(key<target->key)
        insert(target->lchild,key,val);
    else return;//插入的键值已经存在于当前的树中，假设这种情况不存在
}

2、非递归版
如果不用递归，代码会变得复杂一些。

void insert(int key,int val){
    node **scout=&root;
    while(*scout){
        if(key>*scout->key)scout=&(*scout->rchild);
        else scout=&(*scout->lchild);
    }
    *scout=new node(key,val);
}

查询
其实查询操作已经隐含在了插入中。

void query(int key,int val){
    node *scout=root;
    while(scout->key!=key){
        if(key>scout->key)scout=scout->rchild;
        else scout=scout->lchild;
    }
    return scout->val;
}

由于不需要修改节点信息，所以查询操作不需要取址符。
至此，一个二叉查找树诞生了。

class Tree{
    struct node{
        int key,val;
        node(int k,int v){key=k,val=v;}
        node(){}
    };
    node *root;
public:
    void insert(int key,int val){
        node **scout=&root;
        while(*scout){
            if(key>*scout->key)scout=&(*scout->rchild);
            else scout=&(*scout->lchild);
        }
        *scout=new node(key,val);
    }
    void query(int key,int val){
        node *scout=root;
        while(scout->key!=key){
            if(key>scout->key)scout=scout->rchild;
            else scout=scout->lchild;
        }
        return scout->val;
    }
};

实例化后就可以使用了
还可以进一步修改成模板类

template<typename KeyType,typename ValType>
class Tree{
    struct node{
        KeyType key;ValType val;
        node(KeyType k,ValType v){key=k,val=v;}
        node(){}
    };
    node *root;
public:
    void insert(KeyType key,ValType val){
        node **scout=&root;
        while(*scout){
            if(key>*scout->key)scout=&(*scout->rchild);
            else scout=&(*scout->lchild);
        }
        *scout=new node(key,val);
    }
    int query(KeyType key){
        node *scout=root;
        while(scout->key!=key){
            if(key>scout->key)scout=scout->rchild;
            else scout=scout->lchild;
        }
        return scout->val;
    }
};