【NOIP提高组五校联考】道路规划

Description

Solution

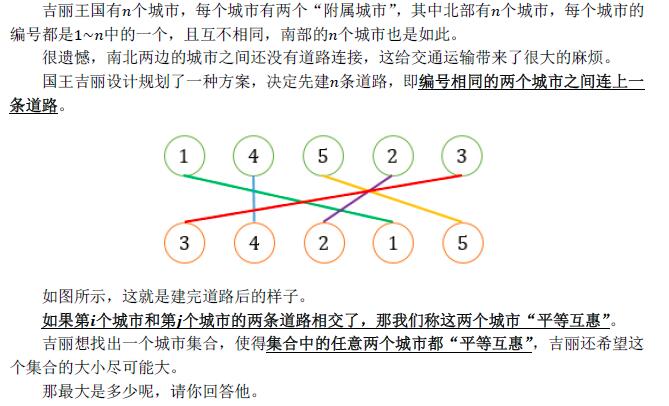
很显然可以把题目转换为相连点的位置作为编号，把两个点投影到坐标轴上能够发现，相交的边在投影出的区间一定是相交的。因为要求的是集合内的每一条边都两两相交，所以满足条件的一定是一个区间被另一个大一点的区间完全包含。容易想到，左端点顺序排序后，右端点做最长下降子序列，最长长度即为答案。

Code

var
    a,b,f:array[0..100000] of longint;
    n,i,sum,wz,x:longint;
function max(x,y:longint):longint;
begin
    if x>y then exit(x) else exit(y);
end;
procedure qsort(l,r:longint);
var i,j,mid:longint;
begin
    i:=l;j:=r;
    mid:=a[(i+j)div 2];
    repeat
        while a[i]<mid do inc(i);
        while mid<a[j] do dec(j);
        if i<=j then
        begin
            a[0]:=a[i];a[i]:=a[j];a[j]:=a[0];
            b[0]:=b[i];b[i]:=b[j];b[j]:=b[0];
            inc(i); dec(j);
        end;
    until i>j;
    if i<r then qsort(i,r);
    if l<j then qsort(l,j);
end;
function get(l,r,x:longint):longint;
var mid:longint;
begin
    get:=0;
    while l<r do
    begin
        mid:=(l+r)div 2;
        if f[mid]>x then
        begin
            get:=mid;
            l:=mid+1;
        end else r:=mid-1;
    end;
    if f[l]>x then get:=l;
    exit(get);
end;
begin
    readln(n);
    for i:=1 to n do read(a[i]);
    for i:=1 to n do
    begin
        read(b[i]);
        f[b[i]]:=i;
    end;
    for i:=1 to n do
    begin
        b[i]:=f[a[i]];
        a[i]:=i;
    end;
    fillchar(f,sizeof(f),0);
    qsort(1,n);
    sum:=1;
    f[1]:=b[1];
    for i:=2 to n do
    begin
        wz:=get(1,sum,b[i]);
        inc(wz);
        f[wz]:=max(f[wz],b[i]);
        if wz>sum then sum:=wz;
    end;
    writeln(sum);
end.