人工智能原理课程复习——（3）搜索策略：盲目搜索

本文链接：https://blog.csdn.net/GOLD1010/article/details/139455867

搜索策略：盲目搜索

影响搜索策略的要素

我们在前文有提到，搜索就是不断地从frontier集合中移除结点，再将子节点加入到frontier的过程

在这个过程中，最重要的就是从frontier中选择哪个结点进行扩展，这就决定了不同的搜索策略

盲目搜索策略

我们在前面提及的搜索都没有考虑当前结点离目标结点的距离

我们称这种搜索为盲目搜索

对于上图而言，上述两个状态都只是搜索过程中的一个结点而已，在盲目搜索中，它们并没有谁优谁劣的比较。

下面我们将介绍几种经典的盲目搜索策略

宽度优先搜索BFS

宽度优先搜索的特点是：每次都从frontier中选取深度最浅的结点进行扩展

并且在将子节点加入frontier前进行目标测试，这是为了能尽量少的扩展下一层

若要将上述改为图搜索版本，只需要在目标测试之前加入重复性判断即可

IF child is not in frontier or explored then：目标测试

宽度优先搜索优先获得的是深度最浅的解，并不是路径代价最短的解

因此如果我们想要路径代价最短的解，就要优先扩展路径代价最小的解

也就是下面将提到的一致代价搜索UCS

一致代价搜索UCS

我们从初始状态S出发，可得下列访问次序

S,p,d,b,e,a,r,f,e,G

这里有两个需要注意的地方

①我们在访问到结点f时，会将f结点的子节点也加入到frontier中，此时就已经能发现目标结点G已经被找到。但如果此时就结束搜索的话，就不能确保找到路径代价最优了，因此我们还需将该目标节点放回到frontier中，再将其从frontier中拿出来进行测试。

②若搜索出的结点与已经存在的结点重复了，此时我们需要选出路径代价最小的。如上图中的两个e,一个代价为5，另一个代价为9.因此我们会去除掉代价为9的结点e，保留代价为5的结点e。若两个结点代价相同，则我们去掉最新的结点，而保留老的结点，如下图所示

该算法的特点在于以下两点

①每次都从frontier选出路径代价最小的结点进行扩展

②每次都在将子节点加入explored集合之前进行目标测试，这样是为了保证路径最优性

③重复处理：即若新节点的状态和explored里的节点状态一样时，那么新扩展出的节点的路径代价一定会大于已经explored的节点的路径代价，故可以直接去除新节点

BFS和UCS的联系

若单步代价相同，则UCS的结点扩展顺序和BFS相同，只是UCS比BFS多扩展一层结点。

它们两者的空间复杂度都非常高。

因此我们需要考虑一个可以降低空间复杂度的方法，即深度优先搜索DFS

深度优先搜索DFS

先来对比一下BFS和DFS两个算法的异同

关于深度优先搜索的目标测试问题，该方法与宽度优先一样可进行提前测试

深度优先树搜索是不完备的。因为即使在有限空间内，可能会出现循环卡死的情况。如A->B->A反复卡在这里，然而在无穷空间处，由于分支因子无限大，因此也可能找不到解。

然而对于深度优先图搜索而言，在有限空间内是完备的，因为它会进行重复性检查。但同样的在无穷空间处仍然是不完备的。

因此深度优先在大部分情况下是不具备完备性的，且对于图搜索会出现无限分支的情况，因此可以考虑深度受限搜索DLS。

深度受限搜索DLS

该算法的主要思想就是限制算法的搜索深度

上面四个填空题分别对应着

Cutoff,Solution,Cutoff,Failure

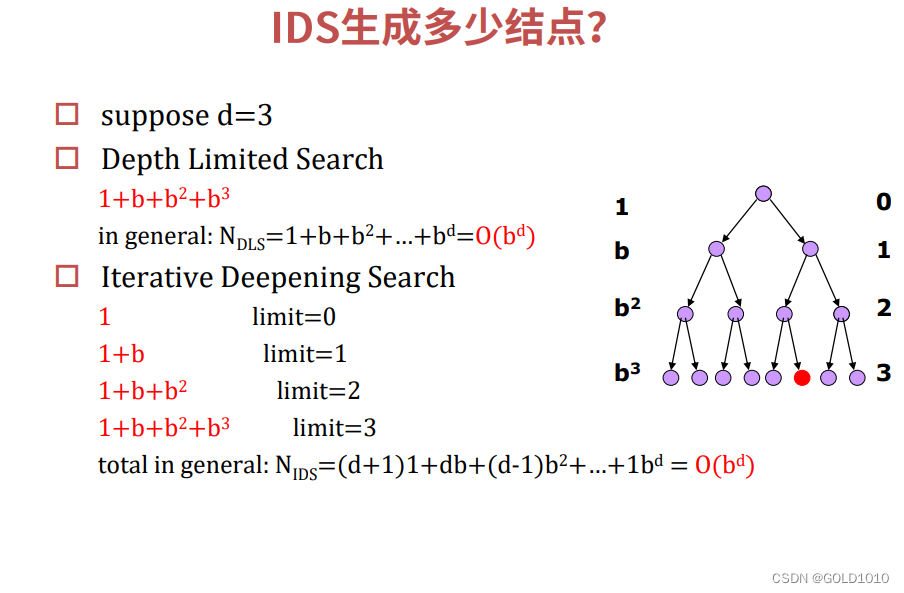
迭代加深搜索IDS

深度优先搜索策略空间复杂度低，但找不到最浅的解。

宽度优先搜索策略可以找到最浅的解，但空间复杂度较高。

因此可以考虑将深度优先搜索策略和宽度优先搜索策略进行混合

这就是迭代加深搜索的主要思想

即每次都使需要搜索的深度加1，因此每次迭代至少会产生上轮迭代的所有解

双向搜索

我们还可以考虑从初始状态出发往目标状态搜索，同时从目标状态出发往初始状态搜索

这就是双向搜索的主要思想

且两个方向都可调用不同的搜索算法

小结

	BFS	UCS	DFS	DLS	IDS	BS
完备性	$Yes^{a}$	$Yes^{a,b}$	$No$	$No$	$Yes^{a}$	$Yes^{a,d}$
最优性	$Yes^{c}$	$Yes$	$No$	$No$	$Yes^{c}$	$Yes^{c,d}$
时间	$O(b^{d})$	$O(b^{1+\left \lfloor \frac{c}{\varepsilon } \right \rfloor})$	$O(b^{m})$	$O(b^{l})$	$O(b^{d})$	$O(b^{\frac{d}{2}})$
空间	$O(b^{d})$	$O(b^{1+\left \lfloor \frac{c}{\varepsilon } \right \rfloor})$	$O(bm)$	$O(bl)$	$O(bd)$	$O(b^{\frac{d}{2}})$
何时进行目标测试	提前测试	正常测试	提前测试
对哪个结点进行展开	深度最小	路径代价最小	深度最大