机器学习算法之决策树

决策树学习

你可能玩过二十个问题游戏，游戏的规则很简单：参与的一个人在脑海里想某个事物，其他的游戏者向这个人提问题，只允许提20个问题，问题的答案只能用对或错回答。问问题的人通过推断分解，逐步缩小待测事物的范围。决策树的工作原理与20个问题类似，用户输入一系列数据，然后给出结果。

1.1 决策树表示法

决策树（Decision Tree）是一种简单但是广泛使用的分类器。通过训练数据构建决策树，可以高效的对未知的数据进行分类。决策数有两大优点：1）决策树模型可以读性好，具有描述性，有助于人工分析；2）效率高，决策树只需要一次构建，反复使用，每一次预测的最大计算次数不超过决策树的深度。图1画出了一颗典型的学习到的决策树。这颗决策树根据天气情况分类“星期六上午是否适合打网球”。例如，下图的实例将被沿着这颗决策树的最左分支向下排列，因而被判定为反例（也就是这棵熟预测这个实例PlayTennis=No）。

1.2决策树学习的使用问题

通常决策树最适合具有以下特征的问题：

• 实例是由(属性-值)对表示的：实例是用一系列固定的值属性和他们的值来描述的。在最简单的决策树学习中，每一个属性取少数的离散值。
• 目标函数具有离散的输出值：图（3-1）的决策树给每个实例赋予一个布尔型的分类（例如，yes和no）。决策树方法很容易扩展到学习有两个以上输出值的函数。
• 可能需要析取的描述：图（3-1）的决策树中，可以析取表达式为(OutLook = Sunny $\bigwedge$ Humidity = Normal)$\bigvee$(Outlook = Overcast)$\bigvee$(Outlook = Rain $\bigwedge$ )。
• 训练数据可以包含错误：决策树学习对错误有很好的健壮性，无论是训练样例所属的分类错误还是描述这些样例值的属性错误。
• 训练数据可以包含缺少属性值的实例：决策树甚至可以在有未知属性值的训练样例中使用（例如，仅有一部分训练样例知道当天的湿度）。

1.3 基本的决策树学习算法

目前大多数的决策树学习算法是一种核心算法的变体，该算法自定向下的贪婪搜索遍历可能决策树空间，这种方法是ID3算法（Quinlan 1986）和后记的C4.5算法（Quinlan 1993）的基础，下面将给出决策树学习的基本算法，和ID3算类似。
基本的ID3算法通过自顶向下的方法个构造决策树来进行学习，构造过程是从“哪一个属性将在树的根结点被测试？”这一问题开始的。使用统计测试来确定每一个实例属性单独分类训练样例的能力。分类能力最好的属性被选作树的根结点的测试。然后为根结点的每个可能值产生一个分支，并把训练样例排列到适当的分支（样例的属性值对应的分支）之下。然后重复整个过程，用每个分支结点关联的训练样例来选取在该点被测试的最佳属性。表1.1是用于学习布尔函数的ID3算法的概要：
———————————————————————————————————————————————
算法1
ID3（Example， Target_attribute, Attributes）
Example为训练集。Target_attribute是树要预测的目标属性。Attributes是出目标属性外供学习到的决策树测试的属性列表。返回一颗能正确分类给定Examples的决策树。

创建树的Root节点
如果Example都为正，那么返回label = + 的单节点树Root
如果Example都为反，那么返回label = - 的单节点树Root
如果Attributes为空，那么返回单节点树Root，label = Examples中最普遍的Target_attribute值
否则开始
A<-Attributes中分类Examples能力最好的属性
   Root的决策属性<-A
   对A的每个可能值v_i
   在Root下加一个新的分支对应测试A = v_i
   令Examples_v为Examples中满足A属性值为v_i的子集
   如果Examples_v为空
    在这个新分支下加一个节点，节点的label=Examples中最普遍的Target_attribute值
    否则在这个新分支下加一个子熟ID3(Examples_v, Target_attribute, Attribute-{A})
结束
返回Root

注：ID3是一种自顶部向下增长树的贪婪算法，在每个节点选取能最好地分类样例属性。继续这个过程直到这棵树能完美分类训练样例，或所有的属性都已被使用过。
——————————————————————————————————————————————

1.4 哪个属性是最佳的分类属性

ID3算法的核心问题是选取在树的每个结点要测试的属性。这里希望选择的是最优助于分类实例的属性。那么衡量属性价值的一个好的定量标准是什么呢？这就是会用到的统计属性，称为“信息增益”(information gain)，用来衡量给定的属性区分训练样例的能力。ID3算法在增长树的每一步使用这个信息增益从候选属性中选择属性。

1. 用熵度量样例的均一性

为了评测那种数据划分方式是最好的数据划分之前，必须学习如何计算信息增益。集合信息度量方式成为香农熵或者简称为熵，这个名字来源于信息之父克劳德·香农。 如果看不明白什么是信息增益和熵，也没关系——它们自诞生那天起，就注定了令人费解。克劳德·香农写完信息论文后，约翰·冯·诺依曼建议使用熵这个术语，因为大家都不知道他是什么意思。

克劳德·香农
克劳德·香农被公认为是二十世纪最聪明的人之一，威廉·庞德斯通在其2005年出版的《财富公式》一书中是这样描写劳德·香农的：贝尔实验室和MIT有很多人将爱因斯坦相提并论，而其他人则认为这种对比是不公平的——对香农是不公平的。”

熵定义为信息的期望值，它刻画了任意样例集的纯度（purity）。给定包含关于某个目标概念的正反样例的样例集S，那么S相对这个布尔型分类的熵为：

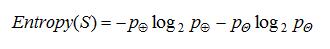
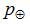
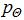
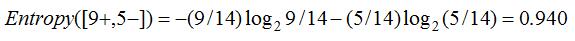
其中，是在S中正例的比例，是S中反例的比例（在所有有关熵的计算中我们定义0log0为0）。假设S是一个关于布尔概念的有14个样例的集合，它包括9个正例和5个反例（我们采用几号[9+，5-]）。那么相对于这个布尔分类的熵为：

注意，如果S的所有成员属于同一类，那么S的熵为0。
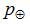
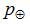
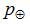
信息轮中对熵的解释是，熵确定了要编码集合S中任意成员（即以均匀的概率随机抽出的一个成员）的分类所需要的最少二进制位数。举例来说，如果是1，接受者知道抽出的样例必为正，所以不必发任何消息，此时的熵为0。另一方面，如果是0.5，必须用一个二进制位来说明抽出的样例是正还是负。如果是0.8，那么对所需的消息编码方法是赋予正例集合较短的编码，可能性较小的反例集合较长的编码，平均每条消息的编码少于1个二进制位。
至此我们讨论了目标分类是布尔型的情况下的熵。更一般地，如果目标属性具有c个不同的值，那么S相对于c个状态(c-wise)的分累的熵定义为：

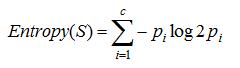
其中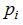，是属于类别的比例，对数的底数仍然为2，原因是熵二进制位的个数来度量编码长度的。
计算熵的代码如下：

#程序清单  计算给定数据集的香农熵
from math import log
def calc_shannon_ent(dataset):
    num_features = len(dataset)
    current_label = {}
    feat_vec = []
    for feat in dataset:
        feat_vec = feat[-1]
        if feat_vec not in current_label:
            current_label[feat_vec] = 0
        current_label[feat_vec] += 1

    shannon_ent = 0.0
    for d in current_label:
        prob = float(current_label[d]) / num_features
        shannon_ent -= prob * math.log(prob,2)
    return shannon_ent

2.用信息增益度量期望的熵降低

已经有了熵作为衡量训练样例集合纯度的标准，现在可以定义属性分类训练数据的能力的度量标准。这个标准被称为“信息增益”。简单地说，一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低。更精确的将，一个属性A相对样例集合S的信息增益Gain（S，A）被定义为：

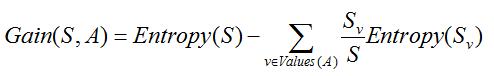
其中，Values（A）是属性A所有可能值的集合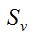，是S中属性A的值为v的子集，所以Gain（S, A）是由于知道属性A的值而导致的期望熵减少。换句话来讲，Gain（S, A）是由于给定属性A的值而得到的关于目标函数值的信息。当对S的一个任意成员的目标值编码时，Gain（S,A）的值是在知道属性A的值后可以节省的二进制的位数。
例如，假定S是有一套有关天气的训练样例，描述它的属性为具有Weak和Strong两个值的Wind。同前面一样，假定S包含14个样例——[9+, 5-]。在这14个样例中，假定正例中的6个和反例中的两个有Wind=Weak，其他的有Wind=Strong。由于按照属性Wind分类14个样例得到的信心增益可以计算如下：

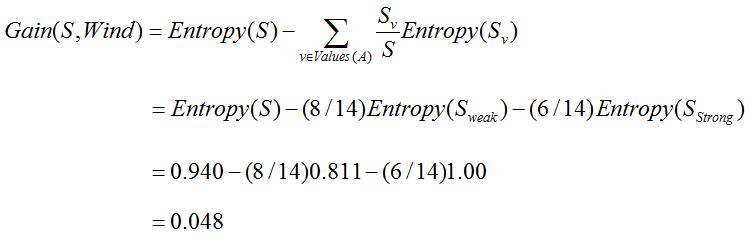
信息增益正是ID3算法增长树的每一步中选取最佳属性的度量标准。下图改善了如何使用信息增益来评估属性的分类能力。在这个图中，计算两个不同属性：湿度（humidity）和风力（wind）的信息增益，以便决定对于分类表的训练样例哪一个属性更好。

未完待续。。。。。