数据结构与算法分析——带有头结点的单链表的实现(C语言)

数据结构与算法分析——带有头结点的单链表的实现

 

表——一种简单的数据结构，有两种实现方式，数组和链表，各有各的优点，用数组来写优点是查找一个元素花费O（1）的时间，缺点是事先并不知道元素个数需要预估的大一些，可能浪费空间，另外删除和插入花费O（N）的时间，用链表写的缺点是查找一个元素需要从头开始查找花费O（N）的时间，优点是采用了不连续存储，插入和删除都避免了线性开销，也不用预估元素个数了，因为在使用表这种数据结构时，会用到大量的插入与删除操作，所以表这种数据结构一般采用链表来实现

链表，每一个结点含有表元素和指向下一个结点的指针，主要操作有查找，插入，删除，大致有两种写法，一种是不带头结点的链表，另一种是带头结点的链表，使用头结点还是有好处的，在插入和删除时避免了对第一个结点的特判，在这里我采用了头结点

我是根据这本书上的函数写的，初次接触链表比较难理解的就是插入和删除这两个操作了，其实在纸上画出来是一个比较好的理解方法，其余的操作都挺简单的，短小精悍。

在单链表实现的基础上又有双向链表和循环链表的扩展，可以避免单链表每次都要从头结点开始查找的缺点，还有一些应用用到了链表，比如多项式、基数排序。

在ACM中，做的题用到链表的不多

代码细节还是挺多的，一次就写成功挺不容易的

 

 

/*
实现一个带有头结点的单链表，
*/
#pragma warning(disable:4996)；
#include<stdio.h>
#include<stdlib.h>

struct Node;
typedef int ElementType;
typedef struct Node *PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;
struct Node {
	ElementType Element;
	Position Next;
};


List MakeEmpty(List L); //生成一个空链表
int IsEmpty(List L);//判断是否为空链表
int IsLast(Position P, List L);//判断是否为最后一个节点
int Length(List L);//返回链表的长度
Position Find(ElementType X, List L);//查找含有元素X的结点
void Delete(ElementType X, List L);//删除含有元素X的节点
Position FindPrevious(ElementType X, List L);//查找含有元素X结点的前驱元
void Insert(ElementType X, List L, Position P);//在P位置之后插入一个结点
void DeleteList(List L);//删除链表
Position Header(List L);//返回头结点
Position First(List L);//返回第一个节点
Position Advance(Position P);//返回该节点的后继元
ElementType Retrieve(Position P);//返回该节点的元素
void Print(List L);//打印链表


List MakeEmpty(List L) {
	if (L != NULL) {
		DeleteList(L);
	}
	L = (List)malloc(sizeof(Node));
	if (L == NULL) {
		printf("out of space\n");
		exit(1);
	}
	L->Next = NULL;
	return L;
}
int IsEmpty(List L) {
	return L->Next == NULL;
}
int IsLast(Position P, List L) {
	return P->Next == NULL;
}
Position Find(ElementType X, List L) {
	Position P;
	P = L->Next;
	while (P != NULL && P->Element != X) {
		P = P->Next;
	}
	return P;
}
Position FindPrevious(ElementType X, List L) {
	Position P;
	P = L;
	while (P->Next != NULL && P->Next->Element != X) {
		P = P->Next;
	}
	return P;
}
void Delete(ElementType X, List L) {
	Position P, TmpCell;
	P = FindPrevious(X, L);
	if (!IsLast(P, L)) {
		TmpCell = P->Next;
		P->Next = TmpCell->Next;
		free(TmpCell);
	}
	else {
		printf("Not Found the Element %d\n",X);
	}
}
void Insert(ElementType X, List L, Position P) {
	Position TmpCell;

	TmpCell = (Position)malloc(sizeof(Node));

	if (TmpCell == NULL) {
		printf("Out of space!\n");
	}

	TmpCell->Element = X;
	TmpCell->Next = P->Next;
	P->Next = TmpCell;
}

void DeleteList(List L) {
	Position P, tmp;
	P = L->Next;
	L->Next = NULL;
	while (P != NULL) {
		tmp = P->Next;
		free(P);
		P = tmp;
	}
}
void Print(List L) {
	Position P = L->Next;
	printf("输出链表所有元素： ");
	while (P != NULL) {
		printf("%d ", P->Element);
		P = P->Next;
	}
	printf("\n");
}
int Length(List L) {
	int Len;
	Len = 0;
	Position P = L->Next;
	while (P != NULL) {
		Len++;
		P = P->Next;
	}
	return Len;
}
Position Header(List L) {
	return L;
}
Position First(List L) {
	return L->Next;
}
Position Advance(Position P) {
	return P->Next;
}
ElementType Retrieve(Position P) {
	return P->Element;
}
int main(void) {
	List L = NULL;
	L = MakeEmpty(L);
	printf("已经创建了一个空表\n");
	if (IsEmpty(L)) {
		printf("该表是一个空表\n");
	}
	Position P;
	P = L;
	for (int i = 1; i <= 5; i++) {
		Insert(i, L, P);
		P = Advance(P);
	}
	printf("链表中共有 %d 个元素\n", Length(L));
	Print(L);
	printf("执行删除0-3的操作\n");
	for (int i = 0; i <= 3; i++) {
		Delete(i, L);
	}
	printf("链表中共有 %d 个元素\n", Length(L));
	Print(L);
	for (int i = 4; i <= 5; i++) {
		printf("%d \n", Retrieve(Find(i, L)));
		if (IsLast(Find(i, L), L)) {
			printf("%d是最后一个元素\n",i);
		}
		else {
			printf("%d不是最后一个元素\n",i);
		}
	}
	DeleteList(L);
	if (IsEmpty(L)) {
		printf("该链表为空表\n");
	}
	getchar();
	getchar();
	return 0;
}

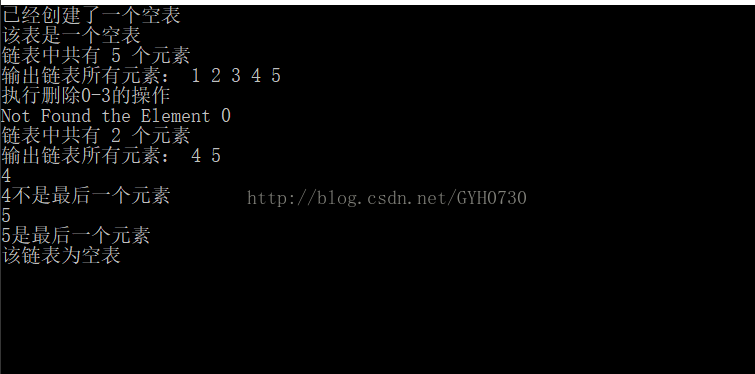
代码验证