纹理的应用（凹凸贴图与法线贴图，三维噪声和三维纹理）

凹凸贴图与法线贴图
在本学期的图形学学习过程中，我发现纹理除了可以表达环境光之外还可以让几何体呈现出凹凸不平形状。这样的纹理称为凹凸贴图，凹凸贴图上定义了每个点的相对高度（高度差）。事实上，凹凸贴图并没有真正的让几何变得凹凸不平，而是通过定义的高度差产生一个假的法线，而法线会影响光照的渲染从而欺骗人的眼睛造成凹凸不平的视觉效果。**凹凸贴图和法线贴图实际上是一回事。**凹凸贴图定义高度差，而法线贴图直接定义法线的位置。

凹凸贴图记录的是高度差，并没有记录法线的位置，如下图黑色的是原几何曲线，而黄色的是根据凹凸贴图得到的扰动后的曲线，那我们如何计算扰动后法线是什么呢？

 

我们先来看一个二维的例子

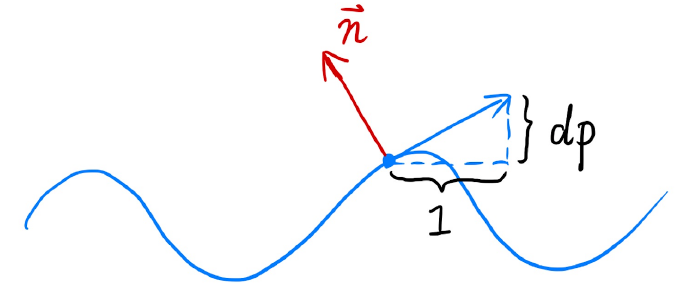
假设在p点，原始法线为(0,1) (0,1)(0,1)，则经过凹凸贴图扰动后p pp点的法线可以通过该点的切线导出（逆时针旋转90度）。根据差分法，可以得到p pp点处的切线dp=c*[h(p+1) - h(p)]，逆时针旋转之后就可以得到法线n(p)=(-dp,1).normalized()。对于三维的情况，我们同样假设原始法线为( 0 ,