P/NP问题

感觉挺有意思的东西，感觉果壳上的一篇文章解释的超级棒;

原文链接：http://www.guokr.com/article/437662/

美剧《基本演绎法》（也就是美版“福尔摩斯”）第 2 季第 2 集中，两位研究 NP 问题的数学家被谋杀了，凶手是同行，因为被害者即将证明“P=NP 问题”，她为独吞成果而下了毒手。然而凶手的动机，并不是千禧年大奖难题那100万美元的奖金——解决了 P=NP 问题，就能够破译世界上所有的密码系统，这里面的利益比100万美元多多了。

剧中只用了一句话来介绍 P=NP 的意义：“能用电脑快速验证一个解的问题，也能够用电脑快速地求出解”。这句过于简单的话可能让大家一头雾水，今天我们就来讲一讲 P vs. NP。

什么是P和NP？

《基本演绎法》S02E02 截图。

计算机科学的一个主要研究方向是提高各种算法的速度。尤其在当前火热的“大数据”概念下，算法速度更显重要。很容易理解，处理的数据越大，计算的耗时就越多。对于一个算法，人们能够分析出运算时间与数据量之间的大致函数关系，这个关系被称为时间复杂度，它定量描述了该算法的运行时间。

假设有 n 个数要排序。一个初级的冒泡排序算法所需时间可能与 n² 成正比，快一点的算法所需时间与 nlog（n） 成正比。在某些条件下，桶排序算法所需时间甚至只和 n 成正比。最不实用的算法就是输入的数字随机排列，直到出现完全有序的情况为止……记前三个算法的时间复杂度分别记为 O(n²)、O(nlogn) 和 O(n)，最后的“猴子排序”(Bogosort)算法平均时间复杂度则达到了 O(n*n!)。

在上面的例子中，前三种算法的复杂度是 n 的多项式函数；最后一种算法的复杂度是 n 的阶乘，根据斯特林公式，n! 相当于指数级别的增长。当 n 特别小时，多项式级的算法已经快过指数级的算法。当 n 非常大时，人类根本看不到指数级复杂度算法结束的那天。自然的，大家会对多项式级别的算法抱有好感，希望对每一个问题都能找到多项式级别的算法。问题是——每个问题都能找到想要的多项式级别的算法吗？

在一个由问题构成的集合中，如果每个问题都存在多项式级复杂度的算法，这个集合就是 P 类问题（Polynomial）。这意味着，即使面对大规模数据，人们也能相对容易地得到一个解，比如将一组数排序。

“NP”的全称为“Nondeterministic Polynomial”，而不是“Non-Polynomial”。NP 类问题指的是，能在多项式时间内检验一个解是否正确的问题。比如我的机器上存有一个密码文件，于是就能在多项式时间内验证另一个字符串文件是否等于这个密码，所以“破译密码”是一个 NP 类问题。NP 类问题也等价为能在多项式时间内猜出一个解的问题。这里的“猜”指的是如果有解，那每次都能在很多种可能的选择中运气极佳地选择正确的一步。

不妨举个例子：给出 n 个城市和两两之间的距离，求找到一个行走方案，使得到达每个城市一次的总路程最短。我们可以这样来“猜测”它的解：先求一个总路程不超过 100 的方案，假设我们可以依靠极好的运气“猜出”一个行走路线，使得总长度确实不超过 100，那么我们只需要每次猜一条路一共猜 n 次。接下来我们再找总长度不超过 50 的方案，找不到就将阈值提高到75…… 假设最后找到了总长度为 90 的方案，而找不到总长度小于 90 的方案。我们最终便在多项式时间内“猜”到了这个旅行商问题的解是一个长度为 90 的路线。它是一个 NP 类的问题。

也就是说，NP 问题能在多项式时间内“解决”，只不过需要好运气。显然，P 类问题肯定属于 NP 类问题。所谓“P=NP”，就是问——是不是所有的 NP 问题，都能找到多项式时间的确定性算法？

P会不会等于NP？

《基本演绎法》S02E02 截图。

这个问题目前还没有定论，当下学术界的大多数意见是 P≠NP。一个主要原因是，这么多年过去了，人们仍然没有找到解决上千个 NPC 问题中任何一个的多项式复杂度的算法。等等，NPC 又是什么？

在与数不尽的问题搏斗的过程中，人们有时候会发现，解决问题 A 的算法可以同时用来解决问题 B。例如问题 A 是对学生的姓名与所属班级同时排序，问题 B 是对人们按照姓名做排序。这时候，我们只需要让班级全都相同，便能照搬问题 A 的算法来解决问题 B。这种情况下，数学家就说，问题 B 能归约为问题 A。

人们发现，不同的 NP 问题之间也会出现可归约的关系，甚至存在这么一类（不只是一个）问题，使得任何其它的 NP 问题都能归约到它们上。也就是说，能够解决它们的算法就能够解决所有其它的 NP 问题。这一类问题就是 NPC 问题。这样的问题人们已经找到了几千个，如果我们给其中任何一个找到了多项式级别的算法，就相当于证明了 P=NP。但是人们至今没有成功找到，所以大家对 P=NP 的信心大打折扣。

解密无遮拦？

《基本演绎法》S02E02 截图。

虽然前景很不乐观，但是不妨来假想一下，如果 P=NP，《基本演绎法》中所说的“破解密码只是小菜一碟”就会成真了吗？

前面说过，证明 P=NP 的一个主要方法就是，给某一个 NPC 问题找到一个快速算法。但是，也不排除有人给出一个“存在性”而非“构造性”的证明，只是告诉大家存在符合要求的算法，但没法详细描述出来。如果 P=NP 被人以这种方式证明出来了，我们也没法依葫芦画瓢地把这个神奇的算法在电脑上写出来，所以对破解密码仍然没有帮助。

退一步说，假如有人构造出可以运用的多项式算法，以此证明了这个问题。这个算法恐怕也很复杂（毕竟这么难找），它的多项式级别的复杂度也可能会非常慢。假设这个算法的复杂度达到了 O(n¹⁰)，那我们依然面临着不小的麻烦。即使 n=100，运算时间也会增长到非常巨大的地步。

再退一步，假设人类的运气好到 P=NP 是真的，并且找到了复杂度不超过 O(n³) 的算法。如果到了这一步，我们就会有一个算法，能够很快算出某个帐号的密码。《基本演绎法》里面所想象的可能就要成真了，所有的加密系统都会失去效果——应该说，所有会把密码变成数字信息的系统都会失去效果，因为这个数字串很容易被“金钥匙”计算出来。

除此之外，我们需要担心或期许的事情还有很多：

• 一大批耳熟能详的游戏，如扫雷、俄罗斯方块、超级玛丽等，人们将为它们编写出高效的AI，使得电脑玩游戏的水平无人能及。
• 整数规划、旅行商问题等许多运筹学中的难题会被高效地解决，这个方向的研究将提升到前所未有的高度。
• 蛋白质的折叠问题也是一个 NPC 问题，新的算法无疑是生物与医学界的一个福音。

Wikipedia上有一个关于NPC问题的列表。如果我们手握解决NPC问题的金钥匙，它们全都能被飞快地解决。

除此之外，P=NP 最令人震撼的成果之一可能是下面这段话：

……(P=NP)会将数学转变为让计算机对任何问题寻找拥有合理长度的证明的学科，因为我们能够在多项式时间内验证一个证明是否正确。这些问题也正好包括千禧年大奖的那些问题。

它出自 NP 完全理论奠基人史提芬·古克的笔下。上面这些只言片语的描述，已经展现出了 P=NP情况下，世界将会出现怎样一副天翻地覆的变化。也正是因为这样的结果实在难以置信，人们普遍倾向于相信 P≠NP。我也希望 P≠NP ，这样至少我的网银相对来说还是挺安全的。

来自wiki的花絮；
话说Hubert Chen的玩笑我想了半天=， =

花絮[编辑]

普林斯顿大学计算机系楼将二进制代码表述的“P=NP?”问题刻进顶楼西面的砖头上。如果证明了P=NP，砖头可以很方便的换成表示“P=NP！”。^[2]

康奈尔大学的Hubert Chen博士提供了这个玩笑式的P不等于NP的证明：^[3]

反证法。设P = NP。令y为一个P = NP的证明。证明y可以用一个合格的计算机科学家在多项式时间内验证，我们认定这样的科学家的存在性为真。但是，因为P = NP，该证明y可以在多项式时间内由这样的科学家发现。但是这样的发现还没有发生（虽然这样的科学家试图发现这样的一个证明），我们得到了矛盾。

以下是一个经典证明：扫雷是NP完全问题

原文链接：
http://www.matrix67.com/blog/archives/544


曾经看到过自动扫雷软件，当时我就在想，扫雷游戏是否有什么牛B的多项式算法。最近才看到，扫雷问题居然是一个NP完全问题，并且这个定理有一个简单、直观而又神奇的证明。在这里和大家分享一下整个证明过程。
    首先，扫雷一定是NP问题，它显然可以在多项式的时间里验证一个解。接下来，我们需要把一个已知的NP完全问题归约到扫雷问题上去。我们将给出一种把逻辑电路问题归约到扫雷问题的方法，这样的话我们就可以利用扫雷问题解决逻辑电路问题，从而说明逻辑电路问题不比扫雷难。我们将把逻辑电路问题转换成一种对应的扫雷布局，就像画画一样把逻辑电路画在扫雷的棋盘上。如果你还不知道什么叫NP完全问题，什么叫逻辑电路问题，你可以看一看我的 这篇文章。

   
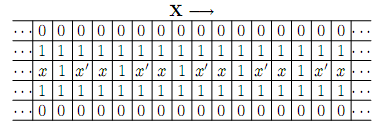
    上图就是一条带有Boolean值的线路。注意到x和x’中有且仅有一个有雷。如果（沿线路方向）前一个格子有雷，我们就说这条线路状态为True；反之如果后一个格子有雷，那么这条线路所传递的Boolean值就是False。每条线路的起始端都如下图左所示，其中符号*表示该格里必然有雷，x和x’中同样是有且仅有一个有雷，但到底是哪一个里面有雷谁也说不清楚。线路是可以拐弯的，如下图右所示，这可以保证转角后Boolean值相同。
   

 
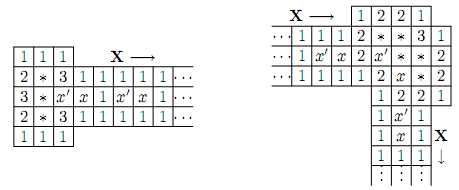
    我们需要构造一些特殊的扫雷布局来解释NOT门、AND门和OR门。构造NOT门最为简单，下图就是一个NOT门，注意经过了中间的NOT门后，x和x’的位置互换，True变成了False，False也将变成True。
   

 
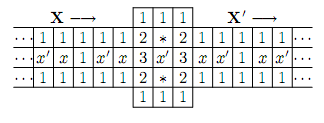
    AND门和OR门的构造就比较复杂了。下面是AND门的构造，U和V是输入的两条线路，T是输出的线路。为了说明这确实是一个AND门，我们将说明：在下面的构造中，如果线路T是True（即最右边那个格子t有雷）的话，那么格子u和v必须都有雷才行。如果最右边的格子t有雷，我们可以很快推断出，图中所有其它的t格都是有雷的，所有t’都是无雷的。观察a3正上方的那个”3″，我们立即看出a2,a3都必须有雷，于是继续推得a1无雷，s有雷。类似地，我们可以知道r也是有雷的。在中间一行的*4t处，4的上下左右都已经有雷了，那么u’和v’必然无雷，于是继续往左推得u和v都有雷。
   

 
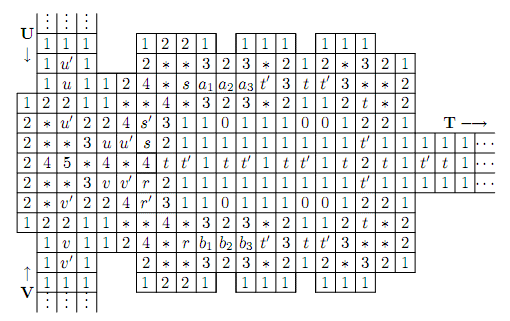
    OR门的构造比较类似，如下图。如果r无雷的话，可知a2,a3有雷，a1无雷，s’有雷，进而s无雷。观察”6″可知u’和v’都有雷，于是u和v均无雷。
   

 
    不断套用这几个逻辑门的构造图来连接电路，直到输出线路只剩下唯一的一条。把最后的输出线路从x或者x’处截断（相当于把最终输出的Boolean值定下来）后，整个布局就成了一个“扫雷版SAT问题”了。
    最后还有一个容易忽略的问题：要是线路交叉了该咋办？下图的构造可以保证线路交叉后仍不改变原线路所带的Boolean值。至此，我们已经可以把任一逻辑电路布局到扫雷棋盘上，解决这个扫雷问题就相当于要解一个逻辑电路问题，因此扫雷问题至少和逻辑电路问题一样难。
   

//话说华为的那题应该是NPC问题，我看了下题目就卒了；