遇事不决，勾股定理

方程是数学、科学和技术的命脉。

方程也是出了名地吓人。斯蒂芬·霍金的出版商告诉他，《时间简史》里每增加一个方程，图书销量就减半一次，E = mc²——这个方程砍掉，《时间简史》能再多卖1000 万本。

但在小学生的作业本上，一排排的等号等待着孩子们的思考，这些等号都是曾经帮助过我们的烛火。

在科学论文里，每一个等号都勇敢地把整个人类文明向前推动了一小步，这些等号是当下正在帮助我们的微光。

在《改变世界的17个方程》这本书里，作者伊恩·斯图尔特带着我们回忆了人类历史上最重要的17个等号。有些等号建立了数量和空间的基本关系，有些等号教会我们用更多的维度看待世界的变化，有些等号指示给我们通往未来生活的路径。17个等号，就是人类一路走来的17个地标、17座丰碑和17盏灯。

《改变世界的17个方程》

[英] 伊恩•斯图尔特

译者：劳佳

“直角三角形中，两条直角边长度的平方之和，等于斜边长度的平方。a²+b²=c² ”

这是连小学生都知道的勾股定律，又叫毕达哥拉斯定理。

它告诉我们什么？

直角三角形的三个边之间有什么关系。

它为什么重要？

提供了几何和代数之间的重要联系，使我们能够根据坐标计算距离。它也催生出了三角学。

它带来了什么？

测绘、导航，以及较近代出现的狭义和广义相对论——现有最好的关于空间、时间和重力的理论。

1

河马上的婆娘

在公元前 570 年左右，毕达哥拉斯出生在爱琴海东部的希腊萨摩斯岛。他是一位哲学家和几何学家。我们对他的生活所知甚少，而且信息都来自很久之后的记述，其历史准确性存疑，但关键事件很可能是对的。公元前 530 年左右，他搬到古希腊殖民地克罗顿（今意大利）。他在那里创立了一个哲学宗教团体——“毕达哥拉斯学派”，他们相信宇宙是基于数字的。时至今日，其创始人的名声就来自以他的名字命名的定理。

关于毕达哥拉斯定理有一个非常流行的笑话，是一个关于“河马上的婆娘”（squaw on the hippopotamus）的糟糕的“谐音梗”。这个笑话在网上随处可见，但是真正的源头就不太可考了。还有关于毕达哥拉斯的漫画、T恤和希腊邮票

尽管说了这么多，我们并不知道毕达哥拉斯是否真的证明了他的定理。事实上，我们根本不知道这是否是他的定理。它完全有可能是毕达哥拉斯的一个仆从，或某个古巴比伦或苏美尔的抄写员发现的。但人们把它归功于毕达哥拉斯，他的名字就流传下来了。无论其起源如何，这个定理和它的结果对人类历史产生了巨大的影响。它们的的确确拓展了我们的世界。

2

直角三角形：三角学宇宙的起源

我们在现实生活中遇到的许多三角形都不是直角三角形，因此方程的直接应用似乎有限。但是，任何三角形都可以分割成两个直角三角形，而任何多边形都可以分割成若干三角形。因此，直角三角形是关键：它们证明了三角形的形状与其边的长度之间存在有用的关系。从这一见解中发展出来的学科是三角学——“三角形的测量”。

直角三角形是三角学的基础，特别是它决定了基本的三角函数：正弦、余弦和正切。这些名称源于阿拉伯语，而这些函数及其许多前辈的发展史，展示了今天这个版本经历了什么样的复杂路径。

直角三角形里当然有一个直角，但另外两个角是任意的，只要加起来是 90° 就行了。任何角都有三个相关的函数——函数就是用于计算相关数字的规则。对于角A，

按常规用a、b、c代表三个边的边长，我们定义正弦（sin）、余弦（cos）和正切（tan）如下：

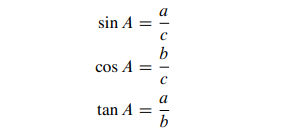
这些量仅取决于角 A，因为给定角 A 的所有直角三角形除了缩放大小不同之外，都是一回事。

因此，我们可以为一系列角度绘制sin、cos和tan值的表格，然后用它们来计算直角三角形的特征。一个可以追溯到远古时代的典型应用，是仅使用在地面上进行的测量来计算高柱的高度。假设从 100 米开外测量，到柱顶的角度是 22°。令图 1.5 中的角 A = 22°，那么 a 就是柱的高度。然后，正切函数的定义告诉我们

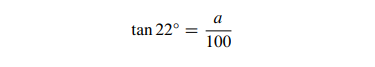
所以

由于 tan 22° 是 0:404（保留小数点后三位），我们就可以得出 a=40:4 米。

一旦有了三角函数，就可以直接将毕达哥拉斯方程扩展到非直角三角形。图 1.6 展示了一个有角度 C 且边长分别为 a、b、c 的三角形。将三角形分成两个直角三角形。然后应用两次毕达哥拉斯方程和一些代数 4，就可证明

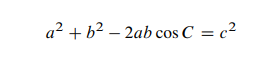
这和毕达哥拉斯方程很相似，除了多出来一项，这个“余弦定理”与毕达哥拉斯方程的作用是一样的，建立了 c 与 a 和 b 之间的联系，但现在必须给出关于角 C 的信息。

余弦定理是三角学的主要支柱之一。如果我们知道三角形的两边和它们之间的夹角，就可以计算出第三边。然后再用类似的方程解出剩下的角度。所有这些方程最终都可以追溯到直角三角形。

3

用三角学计算出地球的大小

测绘学的腾飞是在 1533 年， 当时的荷兰地图制作师赫马 ·弗里修斯（Gemma Frisius） 在 《地点描述小册》（Libellus de LocorumDescribendorum Ratione）中解释了如何使用三角学来获得准确的地图。关于这种方法的消息传遍了整个欧洲，也传进了丹麦贵族和天文学家第谷·布拉赫（Tycho Brahe）的耳朵里。1579 年，第谷用它绘制了其天文台所在的文岛的精确地图。

到 1615 年，荷兰数学家维勒布罗德·斯内利厄斯（Willebrord Snellius，本名维勒布罗德·斯奈尔·范罗恩）将这种方法发展成了现代形式：三角测量法。这种方法用三角形网络测绘区域。通过非常仔细地测量一个初始长度和许多角度，可以计算出三角形顶点的位置，并由此计算出三角形中所有有趣的特征。

斯内利厄斯使用一个由 33 个三角形构成的网络，计算出了两个荷兰城镇阿尔克马尔和贝亨奥普佐姆之间的距离。他之所以选择这两个城镇，是因为它们位于同一条经线上，并且恰好相隔一度。知道了它们之间的距离，他就可以计算出地球的大小。他于 1617 年把这个结果写在了他的《荷兰埃拉托斯特尼》（Eratosthenes Batavus）一书中。他的结果精确到了 4% 以内。他还修改了三角学方程，以反映地球表面的球形特性，这是迈向有效导航的重要一步。

  推荐阅读

作者：伊恩•斯图尔特

译者：劳佳

英国数学科普名家伊恩•斯图尔特经典名作，译为多国语言

李永乐推荐科普读物，“欧拉图书奖”获奖作品

17段改变人类文明进程的数学故事，了解世界运转的深层道理，看懂科学发展的规律