无向图的割点和桥

定义

1. 桥：是存在于无向图中的这样的一条边，如果去掉这一条边，那么整张无向图会分为两部分，这样的一条边称为桥无向连通图中，如果删除某边后，图变成不连通，则称该边为桥。
2. 割点：无向连通图中，如果删除某点后，图变成不连通，则称该点为割点。

在代码 $dfs$ 过程中，加入“时间戳”， $dfs-clock$，
记录到达每个点的时间

pre[u] = ++dfs_clock;

离开每个点的时间

post[u] = ++dfs_clock;

假设无向图如下图：

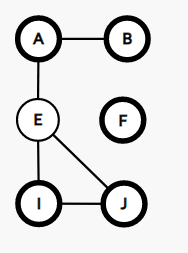
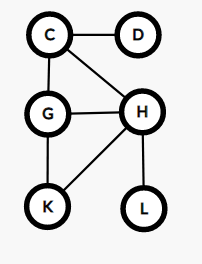
得到的 $DFS$ 树为：

绿色代表树边，红色代表反向边。

定理

在无向联通图 $G$ 的 $DFS$ 树中，非根节点 $u$ 是的割点当且仅当 $u$ 存在一个子节点 $v$ ，使得 $v$ 及其所有后代都没有反向边连回 $u$ 的祖先（连回 $u$ 不算）

假定 $low(i)$ 表示 $u$ 及其后代所能连回的最早的祖先 $pre$ 的值，则定理就可以概括为一句话， $u$ 节点存在一个子节点 $v$ ，使得 $low(i)>=pre(i)$；

代码

int dfs_clock;
int pre[N];
int low[N];             // low(u) 表示 u 及其后代能连回最早的祖先的 pre 值
int iscut[N];           // 判断割顶

int dfs(int u, int fa) {                    // u 在 DFS 树中的结点是 fa
    int lowu = pre[u] = ++dfs_clock;
    int son = 0;                            // 子节点数目
    for(int i = 0; i < G[u].size(); i++){   // 遍历 u 所有子节点
        int v = G[u][i];
        if(!pre[v]){                        // 没有访问过 v
            son++;
            int lowv = dfs(v, u);           // 每次递归返回的就是当前节点的 low() 值
            lowu = min(lowu, lowv);         // 用子节点的 low 值更新 u 的 low 值。
            if(lowv >= pre[u]){             // 判断割顶
                iscut[u] = 1;
            }
        }else if(pre[v] < pre[u] && v != fa)    // 用反向边更新 u 的 low 函数   
            lowu = min(lowu, pre[v]);
        if(fa < 0 && son == 1)                  // 如果是树根且只有一个儿子
            iscut[u] = 0;                       // 不是割顶
        low[u] = lowu;                          // 更新 low 数组
        return lowu;                            // 返回当前顶点的 low 值
    }
}

dfs(rt, -1);