每日算法系列【LeetCode 233】数字 1 的个数

题目描述

给定一个整数 n，计算所有小于等于 n 的非负整数中数字 1 出现的个数。

示例1

        输入：
13
输出：
6
解释：
数字 1 出现在以下数字中: 1, 10, 11, 12, 13 。
      

题解

这题是我搜数位 dp 题目搜出来的，于是我直接用数位 dp 方法把它过了，后来发现其实没必要这么麻烦，简单的计算就能算出来了，这里两个方法我都讲一下。

数学方法

我们不妨用 n = 12345 来举个例子。要求小于等于 n 的数字里有多少个 1 ，我们不妨转换个角度，看某一位数字是 1 的话，有多少数字小于 n 。

例如从右向左数第 i = 2 位（数字 3 ），如果这一位取 1 ，那么左边 2 位如果取 0~11 ，那么右边 2 位就没有任何限制，从 0 取到 99 都行。如果左边 2 位如果取 12 ，那么就得考虑 n 中第 i 位是几了，如果大于 1 ，那么右边 2 位还是没有限制；如果等于 1 ，那么右边 2 位只能取 0~45 ；如果等于 0 ，那就没得取了。

下面这张图是我打的草稿，看的更清楚一点：

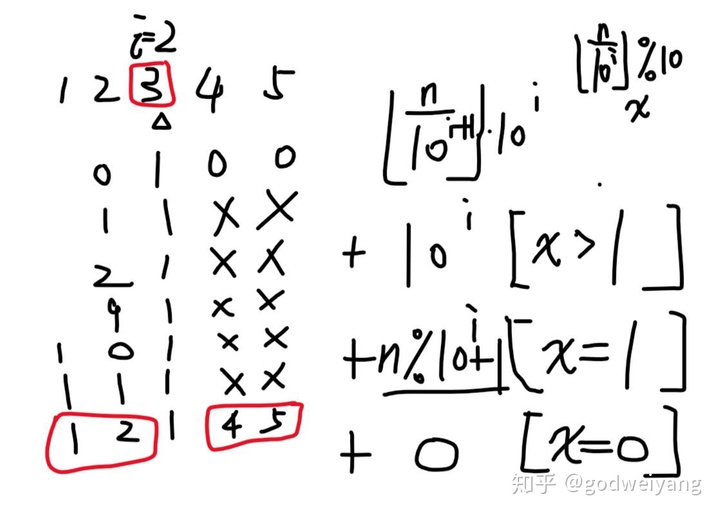
一般化描述就是，考虑从右往左数第 i 位是 1 的数字数量。那么 n 中第 i 位左边部分的数字是 ，而右边可以取的数量是 ，相乘就是总的数量 。如果左边直接取最大值，那么就要考虑第 i 位数字是几了，计算可以得到第 i 位数字为 ，记为 x 。如果 ，那么右边无限制，有 种取法；如果 ，那么右边有 种取法；如果 ，那么右边无法取，因为第 i 位都没法取 1 。

综上，令 ，那么答案就是：