写在前面的话:
本文原地址来自:https://www.topcoder.com/community/data-science/data-science-tutorials/range-minimum-query-and-lowest-common-ancestor/,作者为danielp,若有侵犯相关权益,那就删除吧
本文纯手动翻译,因为感觉网上的翻译实在是……而且我发现原文章上有一个小小的笔误,但是我看的译文都是没有改正的。于是萌发了自己翻译的想法,有些地方可能翻译的不是很到位,还请指出。
转载请注明地址和译者Spica
以下是文章:
目录:
1、 绪论
2、 一些记号
3、 区间最值查询(Range Minimum Query,RMQ)
3-1、RMQ的平凡算法
3-2、一个<O(n),O(sqrt(n))>的解法
3-3、稀疏表(Sparse Table,ST)算法
3-4、线段树
4、 最近公共祖先(Lowest Common Ancestor,LCA)
4-1、一个<O(n),O(sqrt(n))>的解法
4-2、另一个<O(nlgn),O(lgn)>的简单解法
4-3、将LCA归约至RMQ
5、 从RMQ至LCA
6、 一个针对于严格RMQ的<O(n),O(1)>解法
7、 总结
绪论
在一棵有根树上对于一对节点找到它们的最近公共祖先这个问题早在20世纪中叶就已经被仔细的研究过了,现在已经几乎是图论中的基础问题。这个问题的有趣性在于它不仅仅能够被一些巧妙的算法解决,同时它在字符串处理和生物计算上有着大量的应用,比方说LCA可以被用在后缀树或者其他的树状结构当中去。Harel和Tarjan是首先仔细研究该问题的人,他们想出了一种在输入一棵树后,通过线性时间的预处理,便可以在常数时间内求解LCA的询问的办法。他们的工作早就被拓展了,这篇教程将会带来一些同样能够应用在另外一些问题上的有趣的解法。
首先让我们考虑一个不那么抽象的例子:生物树。我们都知道现在地球上的每个物种是由别的一些物种进化而来的。这种关系可以被一棵树来表达,其中点代表物种,点的儿子可以代表和该物种有着直接进化关系的物种。现在把有着相似的属性的物种划分到同一个组里面去。通过在树上查询LCA,我们可以找到某两个物种的公共祖先,然后我们就可以决定他们共有的从父母那儿继承而来的属性。
区间最值查询是用来在一个数组上找到给定的两个位置间的最值的位置。我们稍后将会看到LCA可以被归约至严格RMQ。严格RMQ是指在相邻的数组元素仅仅相差1的特殊数组上的RMQ。
然而,RMQ也不仅仅是同LCA一起使用。它们都在字符串处理中扮演了一个重要的角色,比如说在后缀数组中(译者注:比如在后缀数组中,求解最长回文子串的问题就需要RMQ)。后缀数组是一种在字符串搜索上几乎和后缀树一样快的数据结构,但是它使用更少的内存以及更简单的代码。
一些记号:
假设一个算法需要f(n)的时间预处理和用g(n)的时间处理每一次查询,我们表示这个算法的复杂度是<f(n),g(n)>
在数组A中位置i和j的最小值用RMQA(i, j) 来表示。
在有根树T上离根最远的且又是u和v的共同祖先的用 LCAT(u, v) 来表示
区间最值查询RMQ
(译者注:此处仅仅讨论最小值,但是只要改变序关系即可拓展到最大值等)
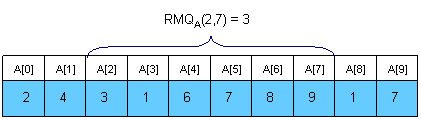
给定一个数组A,找到在给定的两个位置上的最小值的位置
RMQ的平凡算法
对于每一对位置(i,j)都把其 RMQA(i, j) 保存在一个表M[0,n-1][0,n-1]中。这种暴力的计算会导致<O(n^3),O(1)>的复杂度。但是,通过使用一个简单的动态规划可以把复杂度降低到<O(n^2),O(1)>。预处理函数如下:
void process1(int M[MAXN][MAXN],int A[MAXN],int N)
{
int i, j;
for (i =0; i < N;i++)
M[i][i] = i;
for (i = 0; i <N; i++)
for (j = i + 1; j< N; j++)
if (A[M[i][j - 1]]< A[j])
M[i][j] =M[i][j - 1];
else
M[i][j] = j;
}
(译者注:对于区间[i,j],其最小值要么是[i,j-1]上的最小值,要么是j位上的值)
这个算法十分慢,也同时使用了O(n^2)的空间,不适用于大数据。
一个<O(n),O(sqrt(n))>的解法
(译者注:分块)
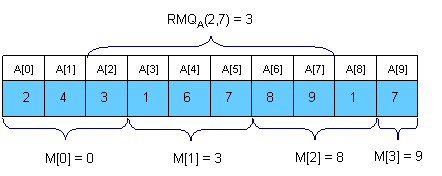
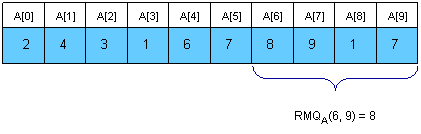
一个有趣的想法就是把这个数组分成sqrt(n)块。我们把每一块的最小值都保存在一个数组M[0,sqrt(n)-1]中。在O(n)的时间内能够轻易的完成M的预处理。例子如下:
现在来看看如何计算RMQA(i, j)。这个想法从首先从所有完全落在区间[i,j]内的块中获取最小值,然后从部分落在区间[i,j]的块中遍历相交的元素来获取最小值。在上面的例子中,为了获取RMQA(i, j),必须要计算A[2],A[M[1]],A[6]和A[7],然后获得最小值的位置。显然对于每次查询不会超过3*sqrt(n)次操作
(译者注:一种简单的最坏情况是考虑n能被sqrt(n)整除,给出的查询区间是[1,n-2]。此时需要获取sqrt(n)-2个中间块,前后各遍历sqrt(n)-1个元素,也就是3*sqrt(n)-2次操作)
这个方法的主要优势在于编程比较简单,同时也可以适用于RMQ的动态版本(指的是你可以在两次查询中修改数组中的元素)
稀疏表(ST)算法
(译者注:动态规划+倍增)
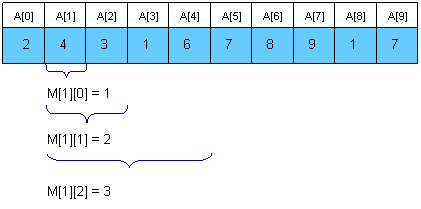
一种更好的预处理RMQ的办法是通过长度为2^k的子数组来使用动态规划。我们维护一个数组M[0,n-1][lgn],其中M[i][j]表示从位置i开始,连续2^j个位置的最小值的位置。例子如下:
为了计算M[i][j]我们必须获取在前一半区间和后一半区间上的最小值。也就是考虑
2^(j-1)的小块,方程如下:
(译者注:实际上就是考虑前2^(j-1)和后2^(j-1)上的最小值)
预处理函数如下:
void process2(int M[MAXN][LOGMAXN], int A[MAXN], int N){
int i, j;
//初始化 M 上长度为1的区间
for (i = 0; i < N; i++)
M[i][0] = i;
//从小区间向大区间计算
for (j = 1; 1 << j <= N; j++)
for (i = 0; i + (1 << j) - 1 < N; i++)
if (A[M[i][j - 1]] < A[M[i + (1 << (j - 1))][j - 1]])
M[i][j] = M[i][j - 1];
else
M[i][j] = M[i + (1 << (j - 1))][j - 1];
}
当预处理完成是,我们来看看如何计算 RMQA(i, j)。想法是选择两个并起来能够覆盖[i,j]的区间,然后在这两个区间上找到最小值,令K=lg(j-i+1)(译者注:均为向下取整)。我们可以用如下的公式来计算
(译者注:选择的这两个区间就算相交也对结果没有影响,只是要保证不会多余或者少于区间[i,j]即可)
因此,一共的时间复杂度是<O(nlgn),O(1)>
线段树
(译者注:这是最简单的线段树了……没有区间修改,仅有区间查询)
解决RMQ问题我们也可以使用线段树来解决。一棵线段树是一个堆状的数据结构,可被用来在对数时间内执行区间更新和查询的操作。我们递归定义区间[i,j]上的线段树如下:
1、 第一个节点维护了区间[i,j]的信息
2、 如果i<j,那么左右儿子分别维护区间[i,(i+j)/2]和[(i+j)/2+1,j]的信息
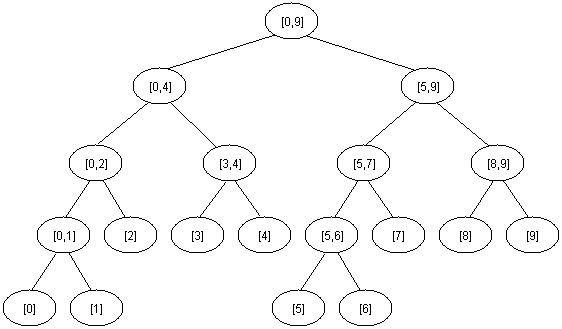
注意到一个有着n个元素的区间的线段树的高度为1+lgn。一棵[0,9]的线段树大概是这个样子
为了使用线段树解决RMQ问题,我们要使用一个数组M[1,2*2^(1+lgn)],其中M[i]表示节点i对应的区间的最小值,起初,M中的所有元素都是-1。可以用下面这个函数来初始化这棵树(b和e是当前区间的界)
void initialize(intnode, int b, int e, int M[MAXIND], int A[MAXN], int N){
if (b == e)
M[node] = b;
else{
//计算左右子树的值
initialize(2 * node, b, (b + e) / 2, M, A, N);
initialize(2 * node + 1, (b + e) / 2 + 1, e, M, A, N);
//找到前一半区间和后一半区间的最小值
if (A[M[2 * node]] <= A[M[2 * node + 1]])
M[node] = M[2 * node];
else
M[node] = M[2 * node + 1];
}
}
上面这个函数隐含了构建这棵树的方法。当计算某个区间的最小值时,我们是通过看子树的值。你在一开始调用这个函数的时候要指定node=1,b=0和e=n-1。
我们现在可以开始进行查询了。假若我们想要找到区间[i,j]的最小值,我们通过下面这个函数:
int query(int node, int b, int e, int M[MAXIND], int A[MAXN], int i, int j){
int p1, p2;
//假若当前的区间和查询区间没有交集,则返回-1
if (i > e || j < b)
return -1;
//假若当前区间被包含在查询区间内,则返回M[node]
if (b >= i && e <= j)
return M[node];
//查询左右子树上最小值的位置
p1 = query(2 * node, b, (b + e) / 2, M, A, i, j);
p2 = query(2 * node + 1, (b + e) / 2 + 1, e, M, A, i, j);
//返回最小值的位置
if (p1 == -1)
return M[node] = p2;
if (p2 == -1)
return M[node] = p1;
if (A[p1] <= A[p2])
return M[node] = p1;
return M[node] = p2;
}
同样的,你应该用node=1,b=0,e=n-1来调用这个函数,因为根节点的区间范围就是这么大。
显然每一次查询都可以在O(lgn)内完成。注意到我们一旦完全落入或者完全脱离查询区间时,便会停止搜索。因此我们在树上搜索的路径一次最多分裂一次。(译者注:最坏情况就是走到最低层节点,比如查询区间[i,i]的时候)
使用线段树我们可以拿到<O(n),O(lgn)>的复杂度。线段树并不仅仅是因为能够解决RMQ问题才是一种十分厉害的数据结构。它十分灵活,同样的也可以解决RMQ的动态版本,在区间搜索的问题上也有许多的应用(译者注:可以支持区间修改,区间查询。甚至能够处理你都想不到的区间问题)
最近公共祖先
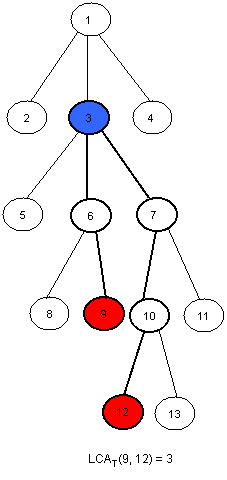
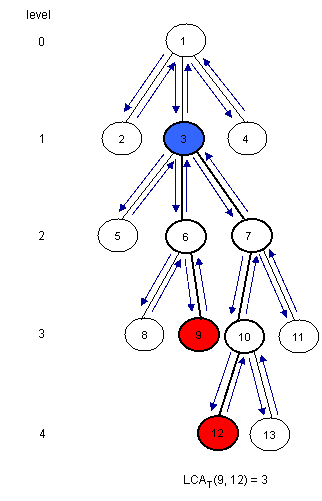
给定一棵有根树T和两个节点u,v。找到一个离根最远的节点且同时又是u和v的共同祖先便是LCA。下面是一个例子
一个<O(n),O(sqrt(n))>的算法
(译者注:看到这个时间复杂度,再联想上面的内容应该就可以猜出来是分块)
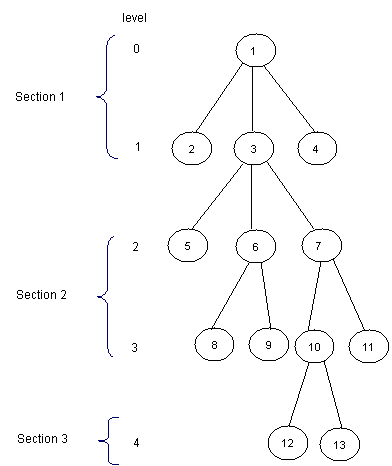
一个有趣的解决RMQ问题的方式是把输入的树分成相等大小的部分。这个分块的办法同样也适用于LCA问题。大概的步骤是把树分成sqrt(H)块,其中H是树的高度。因此,第一块就会包含深度为0~sqrt(H)-1的这些点,第二块就会包含深度为sqrt(H)~2*sqrt(H)-1的这些点,然后以此类推。下面是一个划分的例子
现在,对于每个节点,我们要知道离它最近的且在上一个块的祖先。我们把这个值通过预处理存放在数组P[1,maxn]。比如说上面这个例子的P应该是下图这样(简单起见,第一块的每个节点i,P[i]=1)
注意到某些节点处在它们那些块的最上层,这些节点有着P[i]=T[i]的性质。我们可以通过使用一个DFS来预处理出P (T[i]是节点i的父亲,nr是sqrt(H),L[i]是节点i的深度)
void dfs(int node,int T[MAXN],int N,int P[MAXN],int L[MAXN],int nr) {
int k;
//如果节点位于第一块,就有P[node]=1
//如果节点是处于某些块的最上层,就有P[node]=T[node]
//如果都不是,就有P[node]=P[T[node]]
if (L[node] < nr)
P[node] =1;
else
if(!(L[node] % nr))
P[node] = T[node];
else
P[node] = P[T[node]];
for each son k of node
dfs(k, T,N, P, L, nr);
}
现在我们就可以查询了,为了找出LCA(x, y)我们必须先找到它位于哪一块,然后暴力计算,以下是代码
int LCA(int T[MAXN],int P[MAXN],intL[MAXN], int x,int y){
//只要x和y在上一块的祖先不是同一个
//我们就把深度较深的节点向上提
while (P[x] != P[y])
if (L[x] > L[y])
x =P[x];
else
y = P[y];
//现在x和y是同一块上了,暴力计算LCA
while (x != y)
if (L[x] > L[y])
x = T[x];
else
y = T[y];
return x;
}
这个函数最多做2*sqrt(H)次操作(译者注:考虑一个最深的节点和根节点查询LCA)。这个方法就是一种<O(n),O(sqrt(H))>的算法,其中H是树高。考虑一种最坏情况就是H=n的时候,此时算法就变成了<O(n),O(sqrt(n))>。这个算法的主要优势就是易于编码(平均Division 1的选手不会超过15min)
另一种<O(nlgn),O(lgn)>的解法
(译者注:动态规划+倍增+二分搜索)
我们可以利用动态规划来更快的解决这个问题。首先要计算一张P[1,n][1,lgn]的表,其中P[i][j]表示i的第2^j个祖先。我们可以通过下面这个转移方程来计算
预处理如下:
void process3(int N, int T[MAXN], int P[MAXN][LOGMAXN])
int i, j;
//一开始P中每个元素都是-1
for (i = 0; i < N; i++)
for (j = 0; 1 << j < N; j++)
P[i][j] = -1;
//每个节点的i的第一个祖先都是T[i]
for (i = 0; i < N; i++)
P[i][0] = T[i];
//自下而上地计算
for (j = 1; 1 << j < N; j++)
for (i = 0; i < N; i++)
if (P[i][j - 1] != -1)
P[i][j] = P[P[i][j - 1]][j - 1];
}
该函数消耗O(nlgn)的时间和空间。现在考虑如何查询,令L[i]表示节点i的深度。我们需要注意到的一点就是假若p和q在树的同一层(深度相同),我们就可以通过二分搜索来计算它们的LCA。因此,对于每一个2^j(j从lgn到0,j递减)假若P[p][j]!=P[q][j]我们就可以知道LCA(p,q)在2^j的更上层,因此接下来我们令p=P[p][j],q=P[q][j],继续搜索。最终p和q都会有同样的父亲,此时返回T[p]即可。现在考虑一开始L[p]!=L[q]的情况。不失一般性,假设L[p]<L[q],我们可以同样地使用二分搜索找到和q落在同一深度上的p的祖先,然后我们就可以继续计算LCA(p,q)了。查询函数如下:
int query(int N, int P[MAXN][LOGMAXN], int T[MAXN],
int L[MAXN], int p, int q){
int tmp, log, i;
//假若p的深度小于q,就交换
if (L[p] < L[q])
tmp = p, p = q, q = tmp;
//计算lg(L[p])
for (log = 1; 1 << log <= L[p]; log++);
log--;
//找到和q同一深度的p的祖先
for (i = log; i >= 0; i--)
if (L[p] - (1 << i) >= L[q])
p = P[p][i];
if (p == q)
return p;
//使用表P中的值计算LCA(p,q)
for (i = log; i >= 0; i--)
if (P[p][i] != -1 && P[p][i] != P[q][i])
p = P[p][i], q = P[q][i];
return T[p];
}
该函数最多有2*lg(H)次操作,其中H是树高。最坏情况下就是H=n,因此复杂度就是<O(nlgn),O(lgn)>。这个解法比上一个解法更简单,也更快。
将LCA归约到RMQ
(译者注:通过DFS打上时间戳来转化成在时间戳数组上的查询RMQ,算法导论相关的是“基本的图算法”那一章中的DFS那一小节的”括号化定理”,这里感觉和那边是类似的)
现在让我们来看看如何利用RMQ来计算LCA,事实上,我们可以在线性时间内把LCA归约到RMQ,因此解决RMQ的方法一样也可以解决LCA。通过下面这个例子我们来看看如何归约
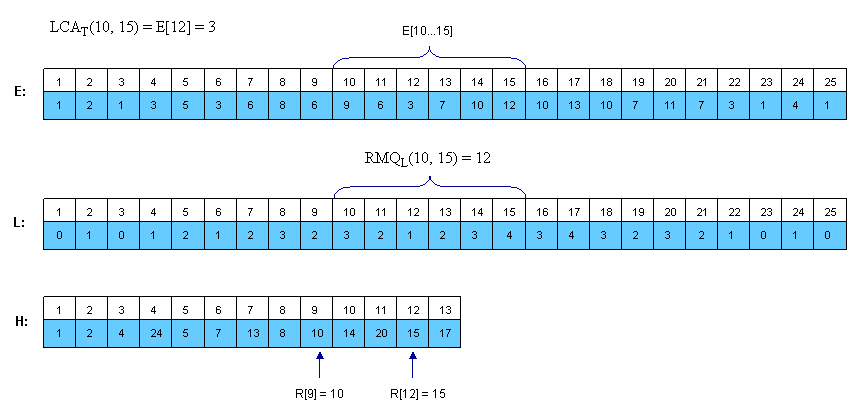
注意到LCA(u,v)是在DFS从u到v的过程中离根最近的节点。考虑任意两个树上的节点u,v在Euler Tour上的位置,然后找到位于这两个位置当中的最小值就可以了。我们需要三个数组来完成这个任务
1、 E[1,2*n-1]表示T的Euler Tour中访问的节点,E[i]代表第i个访问的节点
2、 L[1,2*n-1]Euler Tour访问的节点的深度,L[i]是E[i]节点的深度
3、 H[1,n],其中H[i]是在E中首次遇见节点i的下标(第二次遇见或者第几次遇见都没有关系,这里就考虑第一次)
假定H[u]<H[v](否则就交换u和v)。可以很轻易的看见在第一次遇见u和第一次遇见v之间遇到的节点是E[H[u]……H[v]]。现在我们要在其中找到最小值,这就用RMQ来解决,因此,LCAT(u, v) =E[RMQL(H[u], H[v])] (记住RMQ返回的是下标)。这个例子中的E,L和H如下
我们可以发现L数组相邻的元素仅仅相差1
(译者注:LCA转严格的RMQ就是利用L,实际上可以发现L是E中大小关系的体现,若E[i+1]>E[i],L[i+1]=L[i]+1,反之-1。其实结合DFS的顺序就可以看出来这一点。)
RMQ转LCA
(译者注:实际上牵扯到一个叫做笛卡尔树的东西,笛卡尔树又和Treap有点关系……
,在后面的那张图上其实可以发现仅仅看元素的下标的话,这是一棵二叉搜索树,但是把下标的值带进去的话,这是一个最小堆,这就是Treap的性质了。)
我们已经说明了如何在线性时间内把LCA归约到RMQ上。接下来我们看如何把RMQ归约到LCA上。这意味着我们可以把通常的RMQ转化为严格的RMQ(相邻元素仅仅相差1)。我们需要利用笛卡尔树来完成这个任务。
一个笛卡尔树是数组A[0,n-1]的一个二叉树C(A),其中根是A中的最小元素的下标,无妨用i表示。根的左儿子是A[0,i-1]上的一棵笛卡尔树,若i<=0,则没有左儿子。右儿子的定义很相似,是A[i+1,n-1]的一棵笛卡尔树。要注意的一点就是假若A中存在相同的元素的话,笛卡尔树并不是唯一的。但是我们这儿只用到最小值的第一次出现,因此这里的笛卡尔树是唯一的。可以发现RMQA(i, j) = LCAC(i, j)(译者注:此时问题就集中于建树上面,下面一大段说明的就是如何建树)
例子如下
现在我们只需要在线性的时间内计算出C(A)。这个可以用一个栈来实现
(译者注:这里用的是单调栈,即从栈底到栈顶,某个优先级是递增的,这里的优先级是A[i]的大于关系)。
一开始栈是空的,我们不断的向栈中插入A的元素。第i次插入A[i],在插入A[i]时,所有栈顶上大于A[i]的元素都要被移除,直到栈顶的元素小于等于A[i],此时才插入
(译者注:不熟悉单调栈的话,可能会对于这个单调有疑问,实际上利用数学归纳法,一开始栈空时,是单调的,第一次插入元素时,是单调的,随后每一次插入都保持了单调性,因此整个栈无论在什么时候都有从栈底到到栈顶的优先级递增的单调性)。
在插入时被弹出的那些元素都会按原样成为A[i]的左儿子,而A[i]将会变成那个栈顶小于等于A[i]的栈顶元素的右儿子。
(译者注:不用担心被弹掉的那些分支以后还会被用到,这是不可能的,要证明的话,牵涉到Treap的插入操作,要用到旋转,这里就不赘述了)。
在每一步操作中栈底元素就是当前笛卡尔树的根。假若栈中保存的是元素的下标,而不是值的话,我们建树就会要简单许多。
下面是一个例子来演示在每一次插入的过程中栈是如何变化的
| 序号 | 栈 | 树上的修改 |
| 0 | 0 | 0是树中唯一的节点 |
| 1 | 0 1 | 1 被加入栈顶,现在1是0的右儿子 |
| 2 | 0 2 | 2被加入,1被移除(A[2]<A[1]),现在2是0的右儿子,1是2的左儿子 |
| 3 | 3 | A[3]是目前为止最小的元素,因此栈中所有元素都被弹出,现在3的左儿子是0且3成为了根节点 |
| 4 | 3 4 | 4被入栈,3的右儿子是4 |
| 5 | 3 4 5 | 5被入栈,4的右儿子是5 |
| 6 | 3 4 5 6 | 6被入栈,5的右儿子是6 |
| 7 | 3 4 5 6 7 | 7被入栈,6的右儿子是7 |
| 8 | 3 8 | 8被入栈,之前所有大于A[8]的元素都被移除,现在3的右儿子是8,8的左儿子是4 |
| 9 | 3 8 9 | 9被入栈,8的右儿子是9 |
注意到每一个元素至多入栈和出栈一次,因此这个算法是O(n)的。下面就是实现:
void computeTree(int A[MAXN], int N, int T[MAXN]) {
int st[MAXN], i, k, top = -1;
//一开始栈为空
//第i步插入A[i]
for (i = 0; i < N; i++){
//计算第一个小于等于A[i]的元素的位置
k = top;
while (k >= 0 && A[st[k]] > A[i])
k--;
//如上修改这棵树,T[i]表示i的父亲
if (k != -1)
T[i] = st[k];
if (k < top)
T[st[k + 1]] = i;
//插入A[i],移除所有大于A[i]的元素
st[++k] = i;
top = k;
}
//栈底元素是树根,因此没有父亲
T[st[0]] = -1;
}
一个针对于严格RMQ的<O(n),O(1)>的算法
(译者注:上面已经讲述了RMQ转LCA,LCA中有严格的RMQ,且转换都是线性时间的,只要能够用如上的复杂度解决严格的RMQ,那普通RMQ的最好的复杂度就是<O(n),O(1)>的)
现在我们可以明白普通RMQ通过LCA可以被归约到严格RMQ,即相邻元素仅仅相差1.。我们利用这一点给出一个<O(n),O(1)>的算法。我们现在面临的问题是在数组A[0,n-1]上解决RMQ问题,其中|A[i]-A[i+1]|=1,i=[1,n-1](译者注:此处怀疑原文笔误,应为 A[i]-A[i-1],同时后文也验证了我的想法)。显然A中的前后元素仅仅是+1或者-1。此外一点就是A[i]的旧值就是现在的新A[1],A[2]……A[i]的和再加上A[0]的旧值。不过我们并不需要A的旧值。
(译者注:此处可能会有读者摸不着头脑,不明白A是从哪里来的。我这里是忠于原文翻译的。但是我觉得这里作者的衔接似乎不是那么妥当。我的理解是可以向回看,看到LCA转RMQ的那一小节的末尾,有三个数组E,L,H那儿。那儿是在H数组上查询,实际上在E数组上查询问题也不是很大,比如说查询u,v的LCA,可以变成在E上查第一次进入u~第一次进入v之间的最小值,在上面我同样的也注明过,L可以体现出E的大小关系来,因此也可以在同样地也可以在L上查询,L上查询就是一个严格的RMQ了,可以把那儿的E和L看成这儿的A旧和A新)
为了解决这个严格版的问题,我们同样采取分块,把A划分成长度为L=(lgn)/2的块。令C[i]表示第i个块中最小值,B[i]表示第i个块中最小值的位置。那么C和B长度都为n/L。
现在,我们对C数组采用之前说过的ST算法,消耗的O(n/L*(lg(n/L)))=O(n)的时间和空间复杂度。
(译者注:O(n/L*(lg(n/L)))=O(n/L*(lgn-lgL))=O(n/L*lgn)=O(n))
通过这预处理后,我们在几个块上的查询就是O(1)的。现在剩下的问题就是在一个块内如何查询。注意到一个块的长度L=(lgn)/2,这个长度很小。此外A数组实际上是一个二进制数组 (译者注:前后要么是+1,要么是-1) 。此外大小为L的二进制数组的总个数是2^L=sqrt(n)。然后对于长度为L的每一块,都暴力处理出每一对位置的RMQ存放在表P中,这需要最多需要消耗O(sqrt(n)*L^2)=O(n)
(译者注:实际上这个复杂度是小于O(n)的,O(n)并不是一个准确的上界)
对于表P来说,先要预处理出A中每一块,用0替换-1后的对应的二进制数,把这些数放在一个表T[1,n/L]中
(译者注:可以把表P理解为一个三维数组,第一维对应块,后两位代表区间i~j)
对于询问RMQA(i, j)分为两种情形
1、 i和j在同一个块中,直接利用P和T计算即可
2、 i和j处于不同的块中,这要求我们计算3个值,第一个是i到i所属的块的末尾的最小值,第二个是完全包含在区间i~j的内的块的最小值,第三个是j所属的块的开始到j的最小值。其中第一个和第三个转化为第一种情况,第二种情况由于已经通过ST算法处理过了,也是O(1)的查询,最后返回三个情况的最小值即可
总结
RMQ和LCA是具有密切关联的问题,它们甚至可以被相互归约。许多算法都可以解
决这两个问题,它们也能应用到其他的许多问题里面去
以下是一些有关于线段树,LCA和RMQ的问题
SRM 310 -> FloatingMedian
http://acm.pku.edu.cn/JudgeOnline/problem?id=1986
http://acm.pku.edu.cn/JudgeOnline/problem?id=2374
http://acmicpc-live-archive.uva.es/nuevoportal/data/problem.php?p=2045
http://acm.pku.edu.cn/JudgeOnline/problem?id=2763
http://www.spoj.pl/problems/QTREE2/
http://acm.uva.es/p/v109/10938.html
http://acm.sgu.ru/problem.php?contest=0&problem=155,
参考文献
- “Theoreticaland Practical Improvements on the RMQ-Problem, with Applications to LCA and LCE” [PDF] by Johannes Fischer and Volker Heunn
- “The LCAProblem Revisited” [PPT] by MichaelA.Bender and Martin Farach-Colton - a very good presentation, ideal for quicklearning of some LCA and RMQ aproaches
- “Fasteralgorithms for finding lowest common ancestors in directed acyclic graphs” [PDF] by Artur Czumaj, Miroslav Kowaluk and Andrzej Lingas
译后记:
有觉得翻译得不好的,或者是错误的地方,敬请斧正。才疏学浅,十分抱歉。
CSDN的博客编辑真的很烂。








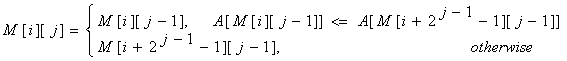
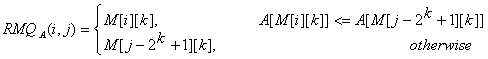

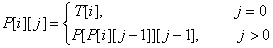
















 1843
1843











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








