LeetCode Day18|● 513.找树左下角的值（左下角理解） ● 112. 路径总和 113.路径总和ii ● 106.从中序与后序遍历序列构造二叉树 105.从前序与中序遍历序列构造二叉树-CSDN博客

本文链接：https://blog.csdn.net/Grace_67/article/details/138704556

day day18 二叉树 part05

day18-1 513.找树左下角的值

如何找到左下角

最后一行 + 最靠左侧的节点（注意：最靠左侧的节点不一定是左孩子）
迭代法要比递归法简单一些
深度最大的叶子节点

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    /**
    * 迭代法
    */
    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int res = 0;
        while(!queue.isEmpty()){
            int size = queue.size();
            for(int i = 0; i < size; i++){
                TreeNode tempNode = queue.poll();
                if(i == 0){
                    res = tempNode.val;
                }
                if(tempNode.left != null){
                    queue.offer(tempNode.left);
                }
                if(tempNode.right != null){
                    queue.offer(tempNode.right);
                }
            }
        }
        return res;
    }
    
     /**
     * 递归法
     */
    private int maxDepth = -1;
    private int resValue = 0;
    public int findBottomLeftValue(TreeNode root) {
        resValue = root.val;
        findLeftValue(root,0);
        return resValue; 
    }
    private void findLeftValue(TreeNode root, int depth){
        if(root ==  null){
            return;
        }
        if(root.left == null && root.right == null){
            if(depth > maxDepth){
                resValue = root.val;
                maxDepth = depth;
            }
        }
        // 左
        if(root.left != null){
            depth++;
            findLeftValue(root.left, depth);
            depth--;
            // 简化版 depth的值没变，但是传入函数的值+1了满足回溯的含义
            // findLeftValue(root.left, depth + 1);  
        }
        // 右
        if(root.right != null){
            depth++;
            findLeftValue(root.right, depth);
            depth--;
        }
    }
}

总结

为啥没有中的处理逻辑，是因为本题没有处理中的逻辑，所有本题前中后序都可以

day18-2 112. 路径总和 113.路径总和ii

大体思路

递归和迭代都可以，但是递归更简单

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
	/**
	 * 递归法（详细版） 精简版可以简化回溯部分的代码
	 */
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root == null){
            return false;
        }
        return traversal(root, targetSum - root.val);
    }
    private boolean traversal(TreeNode root, int targetSum){
        if(root.left == null && root.right == null && targetSum == 0 ){
            return true;
        }
        if(root.left == null && root.right == null){
            return false;
        }
        // 左
        if(root.left != null){
            targetSum -= root.left.val;
            boolean left = traversal(root.left, targetSum);
            if(left){
                return true;
            }
            // 回溯
            targetSum += root.left.val;
        }
        // 右
        if(root.right != null){
            targetSum -= root.right.val;
            boolean right = traversal(root.right, targetSum);
            if(right){
                return true;
            }
            // 回溯
            targetSum += root.right.val;
        }
        return false;
    }
}

day18-3 113.路径总和ii

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) {
            return res;
        }
        List<Integer> path = new LinkedList<>();
        preorderdfs(root, targetSum, res, path);
        return res;
    }
    private void preorderdfs(TreeNode root, int targetSum, List<List<Integer>> res, List<Integer> path){
        path.add(root.val);
        // 遇到叶子节点
        if(root.left == null && root.right == null){
            // 找到了和为 targetSum 的路径
            if(targetSum - root.val == 0){
                res.add(new ArrayList<>(path));// LinkedList放ArrayList中需要转化一下
            }
            // 如果和不为 targetSumm,直接返回
            return;
        } 
        if(root.left != null){
            preorderdfs(root.left, targetSum - root.val, res, path);
            path.remove(path.size() - 1);
        }
        if(root.right != null){
            preorderdfs(root.right, targetSum - root.val, res, path);
            path.remove(path.size() - 1);
        }

    }
}

day18-4 106.从中序与后序遍历序列构造二叉树

构造二叉树的流程

以后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。
流程：

后序数组为0，说明是空节点
后序数组最后一个元素为节点元素
寻找中序数组位置的切割点
切中序数组为左中序+右中序
切后序数组为左后序+右后序
递归处理左区间后区间

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    // 方便根据数值查找位置
    Map<Integer, Integer> map;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        map = new HashMap<>();
        // 用 map 		保存中序序列的数值对应的位置
        for(int i = 0; i < inorder.length; i++){
            map.put(inorder[i], i);
        }
        return findNode(inorder, 0, inorder.length, postorder, 0, postorder.length);
    }
    public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd){
        // 参数里的范围都是前闭右开
        if(inBegin >= inEnd || postBegin >= postEnd){// 不满足左闭右开，说明没有元素，返回空数
            return null;
        }
        // 找到后序遍历的最后一个元素在中序遍历中的位置
        int rootIndex = map.get(postorder[postEnd -1]);
        // 构造结点
        TreeNode root = new TreeNode(inorder[rootIndex]);
        // 保存中序左子树个数，用于确定后序数列的个数
        int lenOfLeft = rootIndex - inBegin;
        root.left = findNode(inorder, inBegin, rootIndex,  
                                postorder, postBegin, postBegin + lenOfLeft);
        root.right = findNode(inorder, rootIndex + 1, inEnd, 
                                postorder, postBegin + lenOfLeft, postEnd - 1);
        return root;
    }
}

注意细节

保证循环不变量，即切割中序数组和后序数组的时候要注意区间，左闭右开？左闭右闭？
先切中序然后再切后序，不然不知道中间的节点（中序里面的左区间和后序里面的左区间相同）

前序和后序构造二叉树？

否，因为只有前序和后序就找不到左右的分割点
图例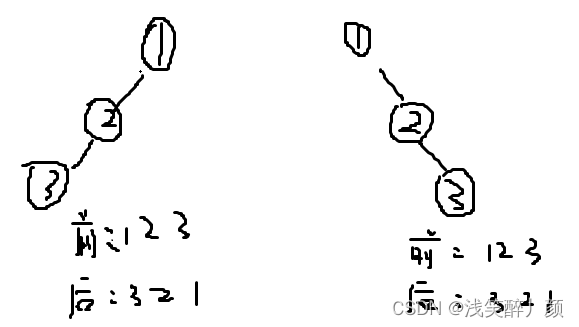：在这里插入图片描述

总结

打流程日志容易排错

day18-5 105.从前序与中序遍历序列构造二叉树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    // 方便根据数组查找位置
    Map<Integer, Integer> map;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        map = new HashMap<>();
        // 用 map 保存中序序列的数值对应的位置
        for(int i = 0; i < inorder.length; i++){
            map.put(inorder[i], i);
        }
        return findNode(inorder, 0, inorder.length, preorder, 0, preorder.length);
    }
    private TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] preorder, int preBegin, int preEnd){
        // 参数里面的范围都是左闭右开
        if(inBegin >= inEnd || preBegin  >= preEnd){
            return null;
        }
        // 找到前序遍历的第一个元素在中序遍历中的位置
        int rootIndex = map.get(preorder[preBegin]);
        // 构造结点
        TreeNode root = new TreeNode(inorder[rootIndex]);
        // 保存中序遍历的左子树用于确定前序数列的个数
        int lenOfLeft = rootIndex - inBegin;
        root.left = findNode(inorder, inBegin, rootIndex, 
                                preorder, preBegin + 1, preBegin + 1 + lenOfLeft);
        root.right = findNode(inorder, rootIndex + 1, inEnd, preorder, preBegin + 1 + lenOfLeft, preEnd);
        return root;
    }
}