笔记——硬币表示

package aaa;

/**
 * 假设我们有八种不同面值的硬币 {1，2，5，10，20，50，100，200}，用这些硬币组合构成一个给定的数值n。
 * 例如n=200，那么一种可能的组合方式为 200 = 3 * 1 + 1 * 2 + 1 * 5 + 2 * 10 + 1 * 50 + 1 * 100.
 * 问总共有多少种可能的组合方式？（这道题目来自著名的编程网站ProjectEuler）类似的题目还有：
 
    [华为面试题] 1分2分5分的硬币三种，组合成1角，共有多少种组合
  1*x + 2*y +3*z=10
    [创新工厂笔试题] 有1分，2分，5分，10分四种硬币，每种硬币数量无限，给定n分钱，有多少种组合可以组成n分钱
 */
public class _9_8硬币表示_经典 {

	public static void main(String[] args) {
		int ways;
		for(int i = 1; i < 16; i++) {
			ways = countWays(i);
			System.out.println(i + "---" + ways);
		}
		for(int i = 1; i < 16; i++) {
			ways = countWay1(i);
			System.out.println(i + "---" + ways);
		}

	}
	
	/**
	 * 递推解法
	 */
	public static int countWay1(int n){
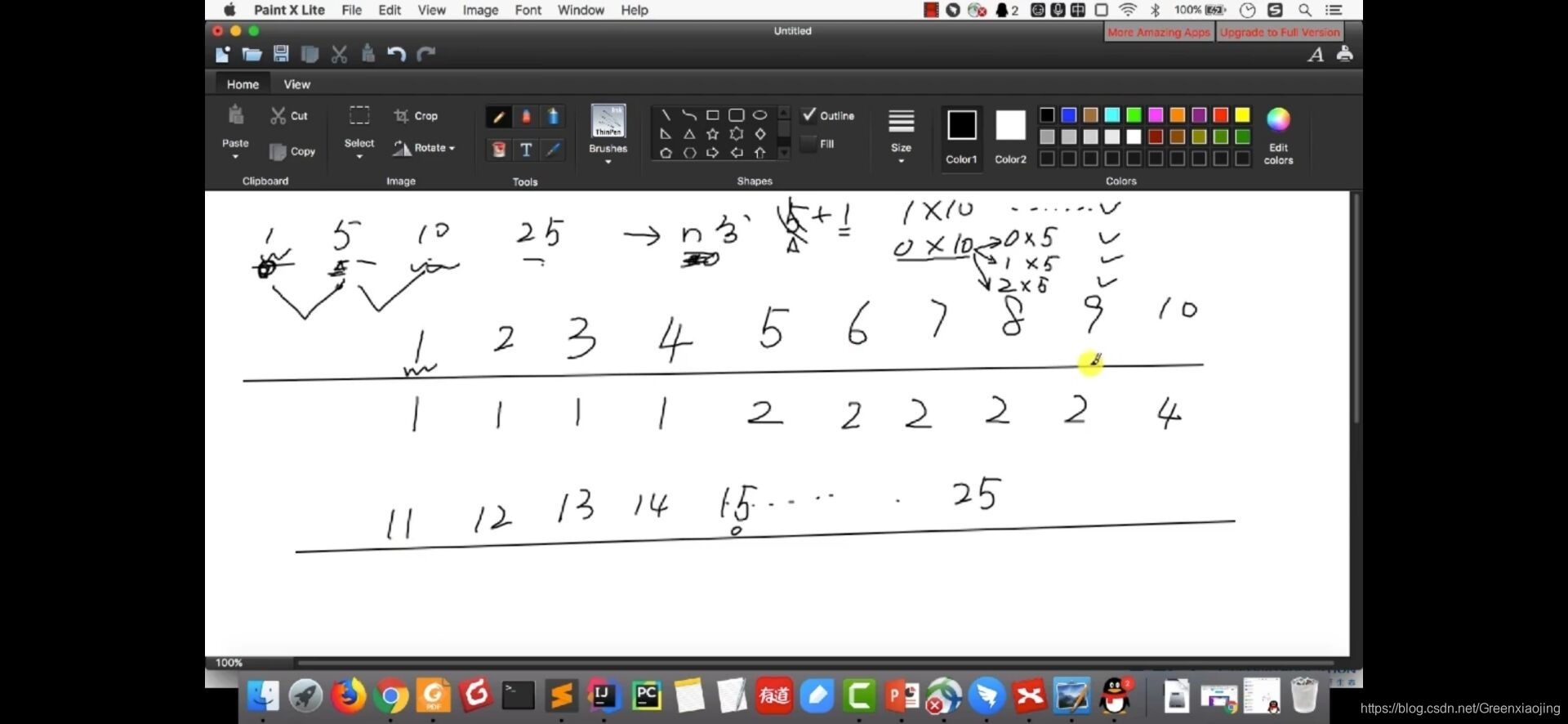
		int[] coins = { 1, 5, 10, 25 };    //四种面值的硬币1,5,10,25
		int[] dp = new int[n + 1];         //值代表的是硬币组成n的方法
		dp[0] = 1;
		for (int i = 0; i < 4; i++) {
			for (int j = coins[i]; j < n+1; j++) {
				dp[j] = (dp[j]+dp[j-coins[i]]) % 1000000007;
			}
		}
		return dp[n];
	}
	
	/**
	 * 递归形式
	 */
	public static int countWays(int n) {
		if(n <= 0) return 0;
		
		return countWaysCore(n,new int[] {1,5,10,25},3);
	}
	private static int countWaysCore(int n, int[] coins, int cur) {
		if(cur == 0) return 1;
		int res = 0;
		//不选coins[cur];
		//要一个
		//要两个.....
		//循环递归 二分到多分支
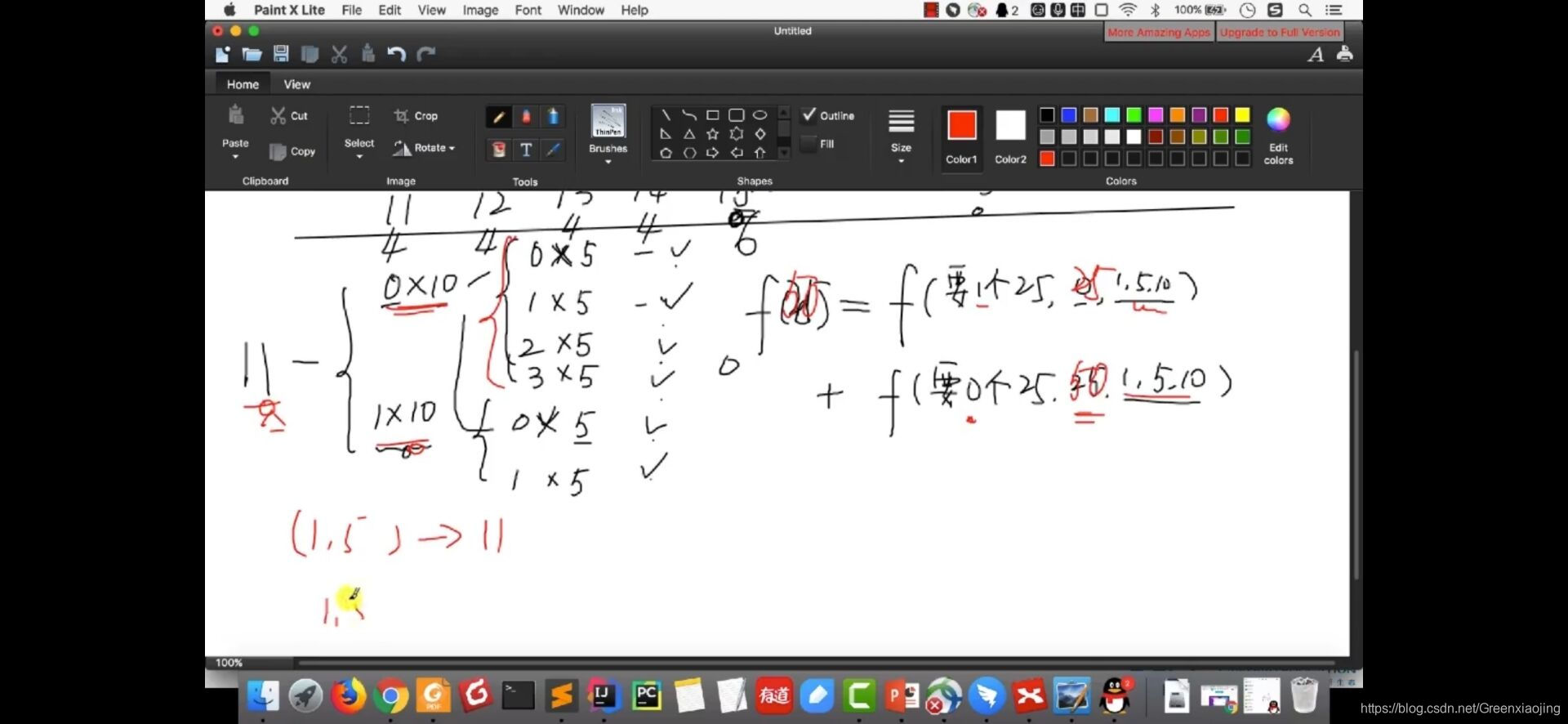
		for(int i=0;i*coins[cur]<=n;i++) {
			int shengyu = n - i*coins[cur];
			res += countWaysCore(shengyu, coins, cur-1);
		}
		return res;
	}

}