26最大流
1.研究的问题
可以把最大流问题用货运公司的运货来模拟。有一个源点持续不断地产生新货物,并通过有限条道路运往一个汇点,每条道路有限定的容量,且进入一个节点的速度和出一个节点的速度相同。求源点到汇点的最大速率。
2.运用算法条件
容量值为非负数,对于两个节点,u,v,(u,v)与(v,u)至多存在一个,如果不连通,令c(u,v)=0,不允许自循环,图必须连通.
c(u,v)指的是容量,f(u,v)指的是流量
3.使实际情况满足条件的修改
(1)解决双向边问题
对于双向边(u,v),添加一个新的节点v’,将c(v,u)=0,连通(v,v’),(v’,u),让它们的容量等于之前的c(v,u)。
(2)解决多个源节点与多个汇点的问题
设立一个超级源节点s和超级汇点t,让超级源节点s到每个源节点的流量为无穷大,设立一个超级汇点,让每个汇点到超级汇点t的流量为无穷大。
三个概念
(1)残存网络
由原图G诱导出来的新图Gf
由那些仍有空间对流量进行调整的边构成
边cf(u,v)=c(u,v)-f(u,v)
为了表示对一个正流量(u,v)的缩减,将边(v,u)加入G,将其残存容量设置为f(u,v),一条边的反向流量最多将其正向流量抵消
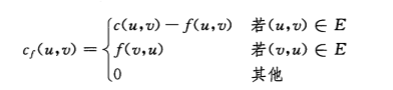


(2)增广路径
一条从源节点s到汇点t的简单路径
残存容量是一条路上最小的cf(u,v)


(3)流网络的切割
最大流最小切割定理:一个流是最大流当且仅当其残存网络不包含任何增广路径。
4.Ford-Fulkerson方法
算法核心:沿着增广路径重复增加路径上的流量,直到没有增广路径为止
算法详解

dfs的思想
以不存在增广路径为终止条件
找到一条增广路径后,设这条路上最小的值为k
将这条路上每条边的值-k,每条边的反向边的值+k
最后终点指向前面各点的值之和即为答案
经典例题
模板题
hdoj1532
第一步:建图
用vector数组建图
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX = 123123;
#define INF 0x3f3f3f3f
struct edge//边的结构体
{
int to, cap, rev;//到达的点,边的容量,反向边
};
vector <edge> G[MAX];//二维
bool used[MAX];//dfs的时候标记是否被访问过
void add_edge(int from, int to, int cap)//建边
{
struct edge a;
//正向建立
a.to = to;
a.cap = cap;
a.rev = G[to].size();
G[from].push_back(a);
//反向建立,反向边
a.to = from;
a.cap = 0;
a.rev = G[from].size()-1;//对应正向边。
G[to].push_back(a);
}
第二步:最大流F-F算法
int max_flow(int s, int t)
{
int flow = 0;//记录要输出的最大流量
for(;;)
{
memset(used, 0, sizeof(used));//标记值清空
int f = dfs(s, t, INF);//找到此时存在的一条边的最大流量
if(f==0)//此时说明已经没有符合的条件了
return flow;//返回最大流量
flow += f;//继续加。。
}
}
第三步:dfs
int dfs(int v, int t, int f)//寻找从v到t的最大流量
{
if(v==t)//找到终点,返回这条路径上的最大流
return f;
used[v] = true;//标记访问过
for(int i=0; i<G[v].size(); i++)//遍历从v出发的每一条边
{
edge &e = G[v][i];//找到这个边
if(!used[e.to]&&e.cap>0)//如果到达的点没有被访问过,并且这条边还可以流水,有容量
{
int d = dfs(e.to, t, min(f, e.cap));//继续dfs,注意最大流量是min(此条边的容量,之前的最小的容量)
if(d>0)//如果存在这条边
{
e.cap -= d;//将容量减少
G[e.to][e.rev].cap += d;//反向边的容量增加
return d;//返回最大流量
}
}
}
return 0;//否则0
}
全部程序
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX = 123123;
#define INF 0x3f3f3f3f
struct edge//边的结构体
{
int to, cap, rev;//到达的点,边的容量,反向边
};
vector <edge> G[MAX];//二维
bool used[MAX];//dfs的时候标记是否被访问过
void add_edge(int from, int to, int cap)//建边
{
struct edge a;
//正向建立
a.to = to;
a.cap = cap;
a.rev = G[to].size();
G[from].push_back(a);
//反向建立,反向边
a.to = from;
a.cap = 0;
a.rev = G[from].size()-1;//对应正向边。
G[to].push_back(a);
}
int dfs(int v, int t, int f)//寻找从v到t的最大流量
{
if(v==t)//找到终点,返回这条路径上的最大流
return f;
used[v] = true;//标记访问过
for(int i=0; i<G[v].size(); i++)//遍历从v出发的每一条边
{
edge &e = G[v][i];//找到这个边
if(!used[e.to]&&e.cap>0)//如果到达的点没有被访问过,并且这条边还可以流水,有容量
{
int d = dfs(e.to, t, min(f, e.cap));//继续dfs,注意最大流量是min(此条边的容量,之前的最小的容量)
if(d>0)//如果存在这条边
{
e.cap -= d;//将容量减少
G[e.to][e.rev].cap += d;//反向边的容量增加
return d;//返回最大流量
}
}
}
return 0;//否则0
}
int max_flow(int s, int t)
{
int flow = 0;//记录要输出的最大流量
for(;;)
{
memset(used, 0, sizeof(used));//标记值清空
int f = dfs(s, t, INF);//找到此时存在的一条边的最大流量
if(f==0)//此时说明已经没有符合的条件了
return flow;//返回最大流量
flow += f;//继续加。。
}
}
int main()
{
int n,m,t;
scanf("%d",&t);
for(int T=1;T<=t;T++)
{
scanf("%d %d", &m, &n);
for(int i=0;i<m;i++)
{
G[i].clear();//注意清
}
for(int i=0; i<n; i++)
{
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
add_edge(a, b, c);
}
int w = max_flow(1, m);//寻找从1到m的最大流量。
printf("Case %d: %d\n",T,w);
}
return 0;
}
5.Edmonds-Karp 算法
EK算法是FF算法的优化,将dfs换成bfs
时间复杂度(v*e^2)
int delta[MaxN]; /* s到i的增广路径上残余流量最小值 */
int pre[MaxN]; /* s到i的增广路径中的上一个点 */
int r[MaxN][MaxN]; /* 残余流量 */
int s, t, n; /* 源点、汇点、点的总数 */
int bfs(){
memset(delta,0,sizeof delta); /* 未访问 */
queue<int> q; q.push(s);
while(not q.empty()){
int x = q.front(); q.pop();
for(int i=1; i<=n; ++i)
if(delta[i] == 0 and r[x][i] > 0){
delta[i] = min(delta[x],r[x][i]);
pre[i] = x;
if(i == t) return delta[t];
/* 已经找到汇点,提前退出 */
q.push(i);
}
}
return 0; /* 无法增广 */
}
int EK(){
int maxFlow = 0;
while(true){
int d = bfs();
if(d == 0) return maxFlow;
for(int i=t; i!=s; i=pre[i]){
r[pre[i]][i] -= d;
r[i][pre[i]] += d;
/* “反对称性” */
}
maxFlow += d;
}
return maxFlow;
}
6.dinic算法
时间复杂度:o(v^2*e)
EK算法的优化
它总是寻找最短的增广路径(通过结点数少),并沿着这条路径更新流。最短增广路径的长度在增广过程中始终不会变短,所以无需每次找增广路前都进行一次bfs。可以先进行一次bfs,按各个点被发现的顺序建立分层图,然后我们在进行dfs找到最短的增广路径,即增广的方向就是先被发现点指向后被发现的点。当没有新的最短增广路径时,意味着需要扩大最短增广路径的长度。此时再进行一次bfs,顺便可以检测是否还有通向汇点的路径。每一次bfs建立分层图的时间复杂度都是O(E),每一步最短增广路径的长度至少增加1,最多增加到∣V∣−1。
int d[MaxN], q[MaxN];
bool bfs(int s,int t){
for(int i=1; i<=n; ++i) d[i] = -1;
d[s] = 0; int *head = q, *tail = q;
*(tail ++) = s;
while(head != tail){
int x = *(head ++);
for(int i=1; i<=n; ++i)
if(d[i] == -1 and c[x][i] > 0){
d[i] = d[x]+1;
*(tail ++) = i;
}
}
return d[t] != -1; /* 存在增广路 */
}
int dfs_T;
int dfs(int x,int inFlow){
if(x == dfs_T) return inFlow;
int sum = 0;
for(int i=1,delta; i<=n; ++i)
if(d[i] == d[x]+1 and c[x][i] > 0){
delta = dfs(i,min(inFlow-sum,c[x][i]));
c[x][i] -= delta, c[i][x] += delta;
if((sum += delta) == inFlow) break;
}
return sum;
}
int dinic(int s,int t){
int maxFlow = 0; dfs_T = t;
while(bfs(s,t)) maxFlow += dfs(s,infty);
return maxFlow;
}
进一步优化:弧优化
在DFS中用cur[x]表示当前应该从x的编号为cur[x]的边开始访问,也就是说从0到cur[x]-1的这些边都不用再访问了,相当于删掉了,达到了满流。DFS(x,a)表示当前在x节点,有流量a,到终点t的最大流。当前弧优化在DFS里的关键点在if(a==0) break;也就是说对于结点x,如果x连接的前面一些弧已经能把a这么多的流量都送到终点,就不需要再去访问后面的一些弧了,当前未满的弧和后面未访问的弧等到下次再访问结点x的时候再去增广。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<long long,long long> pll;
const int inf = 0x3f3f3f3f;
const int maxn=1e3+10;
template<class T>inline void rd(T &x){
x=0;char o,f=1;
while(o=getchar(),o<48)if(o==45)f=-f;
do x=(x<<3)+(x<<1)+(o^48);
while(o=getchar(),o>47);
x*=f;
}
int n;//结点数
int m;//边数
int st;//源点
int ed;//汇点
struct EDGE{
int v;//边指向的结点
int c;//边的权值
int rev;//反向边
};
vector<EDGE>edge[maxn];
int level[maxn];//分层图各个结点的等级
int iter[maxn];//弧优化
void bfs()//一个普通的bfs,记录每个点被发现的顺序
{
queue<int>q;
for(int i=1;i<=n;i++)
level[i]=-1;
level[st]=0;
q.push(st);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=0;i<edge[u].size();++i)
{
EDGE &e=edge[u][i];
if(e.c>0&&level[e.v]==-1)
{
level[e.v]=level[u]+1;
q.push(e.v);
}
}
}
}
int dfs(int u,int f)
{
if(u==ed) return f;
for(int &i=iter[u];i<edge[u].size();++i)//弧优化,标记结点u没有遍历的位置,避免重复搜索
{
EDGE &e=edge[u][i];
if(e.c>0&&level[e.v]>level[u])
{
int d=dfs(e.v,min(f,e.c));//迭代寻找这条路径流的大小。
if(d>0)
{
e.c-=d;
edge[e.v][e.rev].c+=d;
return d;
}
}
}
return 0;
}
int Dinic()
{
int sumflow=0;
while(1)
{
bfs();//预处理,对图分层
if(level[ed]<0) break;//判断是否能连通汇点
memset(iter,0,sizeof(iter));//初始化弧
int addflow;
while(1)//迭代找最短增广路
{
addflow=dfs(st,inf);
if(!addflow) break;
sumflow+=addflow;
}
}
return sumflow;
}
void solve()
{
rd(n);rd(m);//rd(st);rd(ed);
st=1;ed=n;
while(m--)
{
int fr,to,cap;
rd(fr);rd(to);rd(cap);
EDGE in;
in.v=to,in.c=cap,in.rev=edge[to].size();
edge[fr].push_back(in);
in.v=fr,in.c=0;in.rev=edge[fr].size()-1;
edge[to].push_back(in);
}
cout<<Dinic()<<endl;
for(int i=1;i<=n;i++)
edge[i].clear();
return;
}
int main()
{
solve();
return 0;
}

7.isap算法
时间复杂度(v^2*e)
EK算法的优化
加入了标记(算法导论26.4,26.5章内容)
当某一个标记的数目为0时即返回当前流量。循环停止
int c[MAXN][MAXN]; // 残留网络
int d[MAXN]; // d[]:距离标号
int vd[MAXN]; // vd[]:标号为i的结点个数
int S, T, n; /* 源、汇、顶点数 */
int dfs(int i,int inFlow){
// i:顶点, inFlow:最大有多大的流进入i
int j, sum = 0, mind = n-1, delta;
if(i == T) // 到达汇点
return inFlow; /* 返回值为有多大的流进入T */
for(j = 1;j <= n; j++) // 枚举i的邻接点
if(c[i][j] > 0) { // 如果有边到j
if(d[i] == d[j]+1){// (i,j) in E'
delta = dfs(j,min(inFlow-sum,c[i][j]));
/* inFlow-sum:在i点剩下的流量; c[i,j]:这条边的容量 */
// 递归增广,返回沿(i,j)的实际增广量
c[i][j] -= delta; // 更新残留网络
c[j][i] += delta; /* 反对称性 */
sum += delta; // sum记录已经增广的流量
if(d[S] >= n)
// 结束,向上一层返回经过i的实际增广量
return sum;
if(sum == inFlow) break;
// 已经到达可增广上界,提前跳出
}
if (d[j] < mind) mind = d[j];
// 更新最小的邻接点标号
}
if(sum == 0) { // 如果从i点无法增广
vd[d[i]] --; // 标号为d[i]的结点数-1
if(vd[d[i]] == 0) // GAP优化
d[S] = n; /* break标记 */
d[i] = mind + 1; // 更新标号
vd[d[i]] ++; // 新标号的结点数+1
}
return sum; // 向上一层返回经过i的实际增广量
}
int isap(){
int maxFlow = 0;
memset(d,0,sizeof d);
/* 显然,d全部为0是合法的 */
memset(vd,0,sizeof vd);
vd[0] = n; // all vertexes
while(d[S] < n)
maxFlow += dfs(S,INF);
return maxFlow;
}
实际应用
1、裸的最大流
2、二分图的最大匹配:建一个点S,连到二分图的集合A中;建一个点T,连到二分图的集合B中。再将所有的集合A中的点与集合B中的点相连。全部边权设为1,跑一遍最大流,结果即为二分图的最大匹配
由于时间<=500且每个任务都能断断续续的执行,那么我们把每一天时间作为一个节点来用网络流解决该题.
例题:hdoj3572
建图: 源点s(编号0), 时间1-500天编号为1到500, N个任务编号为500+1 到500+N, 汇点t(编号501+N).
源点s到每个任务i有边(s, i, Pi)
每一天到汇点有边(j, t, M) (其实这里的每一天不一定真要从1到500,只需要取那些被每个任务覆盖的每一天即可)用vis数组来达到优化的效果
如果任务i能在第j天进行,那么有边(i, j, 1) 由于一个任务在一天最多只有1台机器执行,所以该边容量为1
最后看最大流是否 == 所有任务所需要的总天数.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<long long,long long> pll;
const int inf = 0x3f3f3f3f;
const int maxn=1e3+10;
struct Edge
{
int from,to,cap,flow;
Edge(){}
Edge(int f,int t,int c,int fl):from(f),to(t),cap(c),flow(fl){}
};
struct Dinic
{
int n,m,s,t;
vector<Edge> edges;
vector<int> G[maxn];
bool vis[maxn];
int cur[maxn];
int d[maxn];
void init(int n,int s,int t)
{
this->n=n, this->s=s, this->t=t;
edges.clear();
for(int i=0;i<n;++i) G[i].clear();
}
void AddEdge(int from,int to,int cap)
{
edges.push_back( Edge(from,to,cap,0) );
edges.push_back( Edge(to,from,0,0) );
m=edges.size();
G[from].push_back(m-2);
G[to].push_back(m-1);
}
bool BFS()
{
queue<int> Q;
memset(vis,0,sizeof(vis));
vis[s]=true;
d[s]=0;
Q.push(s);
while(!Q.empty())
{
int x=Q.front(); Q.pop();
for(int i=0;i<G[x].size();++i)
{
Edge& e=edges[G[x][i]];
if(!vis[e.to] && e.cap>e.flow)
{
vis[e.to]=true;
d[e.to]=d[x]+1;
Q.push(e.to);
}
}
}
return vis[t];
}
int DFS(int x,int a)
{
if(x==t || a==0) return a;
int flow=0, f;
for(int &i=cur[x];i<G[x].size();++i)
{
Edge &e=edges[G[x][i]];
if(d[e.to]==d[x]+1 && (f=DFS(e.to,min(a,e.cap-e.flow) ) )>0)
{
e.flow +=f;
edges[G[x][i]^1].flow -=f;
flow +=f;
a -=f;
if(a==0) break;
}
}
return flow;
}
int max_flow()
{
int ans=0;
while(BFS())
{
memset(cur,0,sizeof(cur));
ans +=DFS(s,inf);
}
return ans;
}
}DC;
int full_flow;
int main()
{
int T; scanf("%d",&T);
for(int kase=1;kase<=T;++kase)
{
int n,m;
scanf("%d%d",&n,&m);
full_flow=0;
int src=0,dst=500+n+1;
DC.init(500+2+n,src,dst);
bool vis[maxn];//表示第i天是否被用到
for(int i=1;i<=n;i++)
{
int P,S,E;
scanf("%d%d%d",&P,&S,&E);
DC.AddEdge(src,500+i,P);
full_flow += P;
for(int j=S;j<=E;++j)
{
DC.AddEdge(500+i,j,1);
vis[j]=true;
}
}
for(int i=1;i<=500;++i)if(vis[i])//被任务覆盖的日子才添加边
DC.AddEdge(i,dst,m);
printf("Case %d: %s\n\n",kase,DC.max_flow()==full_flow?"Yes":"No");
}
return 0;
}
还有一个基于婚配问题的二分图最大匹配做法
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int MAXN=1e2+10;
int n,m,k;//n为男生数,m为女生数
int mp[MAXN][MAXN];
int match[MAXN];//i号女生匹配的男生
bool used[MAXN];//i号女生是否匹配
bool findf(int u)
{
for (int v=0;v<m;v++)
{
if(mp[u][v]&&!used[v])
{
used[v]=true;
if(match[v]==-1||findf(match[v]))
{
match[v]=u;
return true;
}
}
}
return false;
}
int hungary()
{
memset(match,-1,sizeof(match));
int ans=0;
for (int i=0;i<n;i++)
{
memset(used,false,sizeof(used));
if(findf(i))
ans++;
}
return ans;
}
void solve()
{
scanf("%d%d%d",&n,&m,&k);
int u,v,id;
memset(mp,0,sizeof(mp));
while (k--)
{
scanf("%d%d%d",&id,&u,&v);
if (!u||!v)
continue;
mp[u][v]=1;
}
printf("%d", hungary());
return;
}
int main()
{
solve();
return 0;
}
3、最小割:在单源单汇流量图中,最大流等于最小割
4、求最大权闭合图:最大权值=正点权之和-最小割





















 3271
3271











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








