CityHorizon-线段树

题目的大意是：
在一条水平线上有 N 个建筑物，建筑物都是长方形的，且可
以互相遮盖。给出每个建筑物的左右坐标值 Ai,Bi 以及每个建筑物的高度 Hi，
要计算出这些建筑物总共覆盖的面积。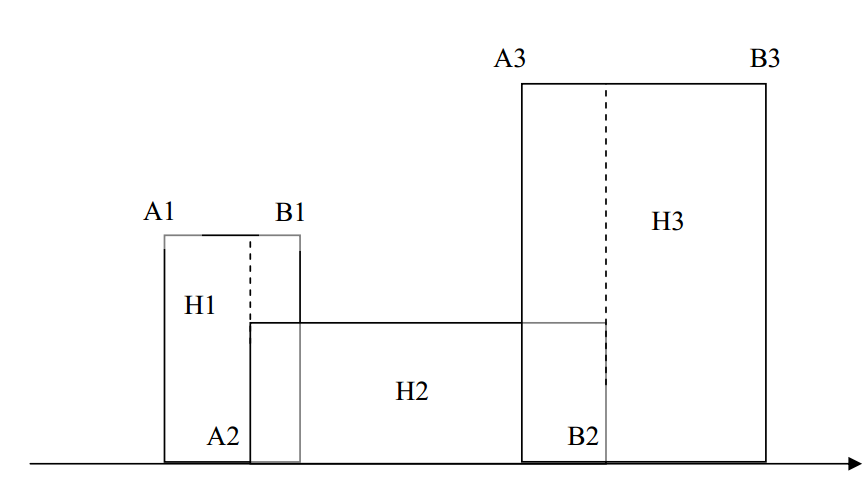
可以将建筑物投影到x轴上 就行成了一段段线段 在线段的基础上要添加权值
权值体现高度的大小 如果同一个线段被覆盖了多次 则以权值大的为准
返回线段的长度乘以权值就可以得到整个建筑物的面积
如果直接对整个的输入构建线段树的话就会花费很大的空间
但是因为输入的案例是少于4000的所以 所有的端点数是少于8000的
在输入了端点以后先把所有的端点进行排序 去除重复的端点 然后按照不重复端点的个数建线段树 在插入线段的时候必须先将线段的两端转化成端点排序后的下标再进行插入 （采用二分搜索来降低复杂度）最后在统计建筑物高度的时候 要将线段树中再转化成对应的端点就可以了。

// CityHorizon.cpp : Defines the entry point for the console application.
//
//input:
//第一行为建筑物的个数 :n
//后面的n行每行包括3个数字 l r h l为建筑物左边界线 r为建筑物右边界线 h为建筑物的高度
//1=<n<=40000 1=<l,r h<=10(9)
//解题思路：
//因为l r 的范围都很大 如果直接构建一个从min(l)~max(r)的线段树的话就会占用很大的内存空间
//所以要先进行离散化的操作 这样最大的构建线段树的长度就是1~80000 
//在线段树中要存储这个线段是否被覆盖 还要存储覆盖当前线段的最大高度
#include "stdafx.h"
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef struct node {
    int nl;
    int nr;
    int nh;
    bool cover;
}Node;
Node  *segtree;
int *r;
int *l;
int *h;
/*
构造线段树
*/
void BuildSegTree(int num, int l, int r)
{
    segtree[num].nl = l;
    segtree[num].nr = r;
    segtree[num].cover =false;
    segtree[num].nh = 0;
    int mid = (l + r) / 2;
    if (r-l != 1)
    {
        BuildSegTree(num * 2, l, mid);//构建左子树 统计范围【l,mid)
        BuildSegTree(num * 2 + 1, mid, r);//构建右子树，统计范围【mid,r)
    }

}
/*
将区间信息在线段树中插入
num当前搜索节点的编号 [l~r)为左右区间 h为区间上的高度
*/
void Insert(int num, int l, int r, int h)
{
    if (segtree[num].nl == l&&segtree[num].nr == r)//恰好覆盖 则停止向下搜寻
    {
        if (segtree[num].nh < h)//如果两段覆盖了同一区域 则以高度以最高的高度为准
        {
            segtree[num].nh = h;
            segtree[num].cover = true;
            return;
        }
    }
    int mid = (segtree[num].nl +segtree[num].nr) / 2;
    if (r <= mid)
        Insert(2 * num, l, r, h);
    else if (l >= mid)
        Insert(2 * num + 1, l, r, h);
    else
    {
        Insert(num * 2, l , mid, h);
        Insert(num * 2 + 1, mid, r, h);
    }
}

/*
删除从l到r的覆盖
如果删除了没有覆盖的地方则函数会返回false
注意线段树中的删除操作都是将相应的线段下降到叶子节点删除的
而且将原来覆盖的节点也是下降到叶子节点 
如果叶子节点原来被覆盖了则返回true 
           没有被覆盖则会返回false
只要将所有叶子节点的返回信息相与就能得到要删除线段原先是否被覆盖
*/
bool del(int num, int l, int r)
{
    if (segtree[num].nr - segtree[num].nl == 1)//把删除的部分转移到叶子节点进行 将所有的叶子节点信息相与 如果原先的节点没有没覆盖则返回false 与后还是false 
    {
        bool temp = segtree[num].cover;
        segtree[num].cover = false;
        return temp;
    }
    if (segtree[num].cover)//搜索到了当前节点就说明当前节点的一部分需要被删除 如果当前节点被覆盖了 则将当前节点置为不覆盖 将子节点置为覆盖 
    {
        segtree[num].cover = false;
        segtree[num * 2].cover = true;
        segtree[num * 2 + 1].cover = true;
    }
    int mid = (segtree[num].nl + segtree[num].nr) / 2;
    if (r <= mid)return del(num * 2, l, r);
    else if (l >= mid)return del(num * 2 + 1, l, r);
    else
    {
        return del(num * 2, l, mid)&&del(num * 2 + 1, mid, r);
    }

}

/*
计算从[l~r）这个范围内的覆盖面积
在计算的时候必须将整个线段树全部的都遍历一遍
因为父节点区间肯定包含了子节点的区间 但是子节点可能也被覆盖了
而且子节点的高度可能大于父节点的高度 所以在计算面积的时候必须从上到下去更新高度
如果父节点被覆盖了且高度大于子节点的高度 则用父节点的高度来替换子节点的高度 
到了最下面一层被覆盖的叶子节点 高度坑定是最高的  
h是num节点父节点的高度
num为当前计算的节点
*/
int calculate(const vector<int>& myhash,int h,int num)
{
    if (h > segtree[num].nh)//如果父节点的高度大于子节点的高度 则更新子节点的高度
        segtree[num].nh = h;
    if (segtree[num].nr - segtree[num].nl == 1) //如果到了叶子节点 且叶子节点被覆盖了则返回叶子节点覆盖区域的面积
    {
        return (myhash[segtree[num].nr] - myhash[segtree[num].nl])*segtree[num].nh;
    }
    return calculate(myhash,segtree[num].nh, num * 2) + calculate(myhash,segtree[num].nh, num * 2 + 1);


}
/*
二分查找找到value对应的元素下标
参数说明：
 v:包含元素的向量
 value：要查找的值
 begin:左下标边界
 end:右下标边界
 返回值为 value在v中的下标
*/
int myfind(vector<int> v, int value, int begin, int end)
{
    if (begin <= end)
    {
        int mid = (begin + end) / 2;
        if (v[mid] == value)
            return mid;
        else if (v[mid] > value)
            return myfind(v, value, begin, mid-1);
        else
            return myfind(v, value, mid + 1, end);
    }

}


int main()
{
    int n;
    vector<int> v;
    cin >> n;//输入线段的个数
    l = (int *)malloc((n + 4)*sizeof(int));
    r = (int *)malloc((n + 4)*sizeof(int));
    h = (int *)malloc((n + 4)*sizeof(int));
    segtree = (Node*)malloc(6* n*sizeof(Node));
    v.push_back(0);//v中的0下标不使用
    for (int i = 1; i <= n; i++)
    {
        cin >> l[i];
        cin >> r[i];
        cin >> h[i];
        v.push_back(l[i]);
        v.push_back(r[i]);

    }
    sort(v.begin()+1, v.end());//下标为0的元素不使用 对下标为1的元素到最后一个元素排序
    v.erase(unique(v.begin() + 1, v.end()), v.end());//擦除下标为1到最后一个元素中重复的元素
    for (int i = 1; i < v.size(); i++)
    {
        cout << i << " " << v[i]<<endl;
    }
    cout << "v.size" << v.size();
    BuildSegTree(1, 1, v.size()-1);//建线段树  线段树包含的范围是[1，v.size()-1] 用v.size()-1因为为了从下标1开始 在下标0处加入了一个0
    for (int i = 1; i <= n; i++)//将原始的输入线段离散化 并插入线段树
    {
        int ml, mr;
        ml = myfind(v, l[i], 1, v.size() - 1);//查找到l[i]所对应的 在已经排好序的v中的下标
        mr = myfind(v, r[i], 1, v.size() - 1);//查找到r[i]所对应的 在已经排好序的v中的下标
        cout << "Insert " << l[i] << ":" << ml << " " << r[i] << ":" << mr << " H:" << h[i] << endl;
        Insert(1, ml, mr, h[i]);
    }
    cout<<"Size: "<<calculate(v, segtree[1].nh, 1)<<endl;

    delete[] l;
    delete[] r;
    delete[] h;
    delete[] segtree;
    system("pause");
    return 0;
}