目录
ID:HL_5461
一、十进制数的指数表示形式
对于一个十进制数,我们可以 把它以科学计数法进行如下表示:
eg.
即:(+/-)的形式(
为系数,
为底数,
为指数),其中系数
相对应的,对于一个十进制数,我们还能有如下表示:
eg.
即:(+/-)的形式(
为系数,
为底数,
为指数),其中系数
如下表格希望能帮助大家更好理解
| 十进制数 | 指数表示 | 符号 | 系数 | 底数 | 指数 | 小数 |
| 0.0066 | + | 6.6 | 10 | -3 | 0.6 | |
| 0.0066 | + | 1.6869 | 2 | -8 | 0.6869 |
这种类型,计算机存储起来是比较困难的,所以计算机对于浮点的存储采用
这种形式
知道了存储形式,现在我们将面临以下三个问题:
1.如何表示符号
2.如何表示指数
3.如何表示系数
二、符号、指数、系数的二进制表示方法
1.如何表示符号
浮点型的符号表示和整型是一样的,都是将左边第一位作为符号位,1为+,0为-,以单精度浮点型为例:
| 二进制数 | 符号 |
| 1000 0000 0000 0000 0000 0000 0000 0000 | + |
| 0000 0000 0000 0000 0000 0000 0000 0000 | - |
2.如何表示指数
我们将符号位的后几位作为指数位,其中单精度浮点型8位,双进度浮点型11位
同时,为了表示负指数,引入了偏移量这个概念(偏移量:单精度浮点型127,双进度浮点型1023),指数=指数位-偏移量
我们举例说明:
| 精度 | 指数位 | 指数位转为十进制数 | 偏移量 | 指数 (指数位-偏移量) |
| 单精度浮点型 | 000 0011 0(共8位) | 6 | 127 | 6-127=-121 |
| 双精度浮点型 | 000 0000 0110 (共11位) | 6 | 1023 | 6-1023=-1017 |
3.如何表示系数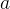
系数是一个在范围
之间的数,所以我们只需表示出小数部分,再将小数部分加一,就可以得到我们所需要的系数
,所以我们的问题就由“如何表示系数
”变为了“如何表示小数部分”。
(注:非规格化数系数的小数点前一位不是1而是0,用0.f表示,但属于比较少见的情况,在此我们不作讨论)
指数位之后的数字都作为小数位,对于小数位的表示采用与整型不一样的表示方法。将小数位从左至右依次作为,
,
……以此推类直至最后一位
我们还是以一张表格来举例:
| 精度 | 小数位 | 小数位转为十进制 | 系数 (小数位+1) |
| 单精度(32bit) | 111 0000 0000 0000 0000 0000(共23位) | 1.875 | |
| 双进度(64bit) | 1110 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000(共52位) | 1.875 |
由此我们不难看出,对于浮点型,计算机一般就是在去通过这个足够长的序列,使得误差保持在一个足够小的范围,并不能保证绝对的精准。
三、总结
最后,我们通过一张表来总结一下:
| 精度 | 符号位 | 指数位 | 偏移量 | 小数位 |
| 单精度 | 1(1位) | 8(2~9位) | 127 | 23(10~32位) |
| 双精度 | 1(1位) | 11(2~12位) | 1023 | 52(13~64位) |
若有错误,欢迎大家批评斧正!






















 1027
1027

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










