DFS&BFS

import java.util.Iterator;


public class Queue<T> implements Iterable<T> {
    //记录首节点
    private Node<T> head;
    //记录最后一个节点
    private Node<T> last;
    private int N;



    private class Node<T> {
        private T item;
        private Node<T> next;
        public Node(T item,Node<T> next){
            this.item = item;
            this.next = next;
        }
    }
    public Queue(){
       this.head = new Node<T>(null,null) ;
       this.last = null;
       this.N = 0;
    }
    public boolean isEmpty(){
        return N==0;
    }
    public int size(){
        return N;
    }
    //向队列中插入元素
    public void enqueue(T t){
        //当前尾节点last为null
        if(last==null){
            last = new Node<T> (t,null);
            head.next = last;
        }else{
            Node<T> oldLast = last;
            last = new Node<T>(t,null);
            oldLast.next = last;
        }
        N++;
        //当前尾节点last不为null
    }
    //从队列中拿出一个元素
    public T dequeue(){
        if(isEmpty()) return null;
        Node<T> oldFirst = head.next;
        head.next = oldFirst.next;
        N--;
        //因为出队列其实是在删除元素,如果队列中的元素删除完了,需要充值last=null;
        if(isEmpty()) last = null;
        return oldFirst.item;
    }

    @Override
    public Iterator iterator() {
        return new QIterator();
    }
    private class QIterator implements Iterator{
        private Node<T> n;
        public QIterator(){
            this.n = head;
        }
        
        @Override
        public boolean hasNext() {
            return n.next != null;
        }
        
        @Override
        public T next() {
            n = n.next;
            return n.item;
        }
    }

    
}

public class Graph {
    //顶点数目
    private int v;
    //边的数目
    private int E;
    //邻接表
    private Queue<Integer>[] adj;
    public Graph(int v) {
        //初始化顶点的数量
            this.v = v;
        //初始化边的数量
            this.E = 0;
        //初始化邻接表
        this.adj = new Queue[v];
        for (int i = 0; i < adj.length; i++) {
            adj[i] = new Queue<Integer>();
        }
    }
    //获取顶点的数目
    public int v(){
        return v;
    }
    //获取边的数目
    public int E(){
        return E;
    }
    //向图中添加一条边v-w
    public void addEdge(int v,int w){
        //在无向图,需要让w出现在v的邻接表中,并且还要让v出现在w邻接表中
        adj[v].enqueue(w);
        adj[w].enqueue(v);
        //变得数量加一
        E++;
    }
    //获取顶点和顶点v的相邻的所有顶点
    public Queue<Integer> adj(int v){
        return adj[v];
    }
    
}

import com.example.demo.code10.queue.Queue;


public class DepthFirstSearch {
    //索引代表顶点,值代表当前顶点是否被搜索
    private boolean[] marked;
    //记录有多少顶点与s顶点相通
    private int count;

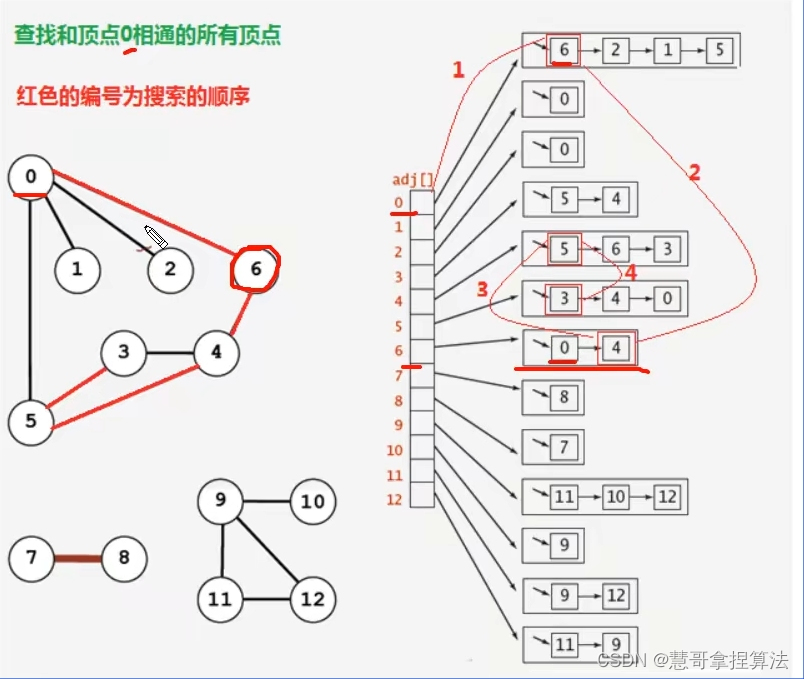
    public DepthFirstSearch(Graph g,int s) {
        //初始化marked数组
        this.marked = new boolean[g.v()];
        //初始化跟顶点s相通的顶点的数量
        this.count = 0;
        System.out.print(s+" ");
        dfs(g,s);
    }

    private void dfs(Graph g, int s) {
        //把s顶点标识为已搜索
        marked[s] = true;
        for (Integer w : g.adj(s)) {
            //判断当前w顶点有没有搜索过,若没有,则递归调用dfs进行深度优先搜索
            if(!marked[w]){
                dfs(g,w);
                System.out.print(w+" ");
            }
            
        }
        //相通顶点数量+1
        count ++;
        
    }
    //判断w顶点和s顶点是否相撞
    public boolean marked(int w){
        return marked[w];
    }
    //获取与顶点s相遇的所有顶点总数
    public int count(){
        return count;
    }
    

}

public class DepthFirstSearchTest {
    public static void main(String[] args) {
        //创建图
        Graph graph = new Graph(13);
        graph.addEdge(0,5);
        graph.addEdge(0,1);
        graph.addEdge(0,2);
        graph.addEdge(0,6);
        graph.addEdge(5,3);
        graph.addEdge(5,4);
        graph.addEdge(3,4);
        graph.addEdge(4,6);
        graph.addEdge(7,8);
        graph.addEdge(9,11);
        graph.addEdge(9,10);
        graph.addEdge(9,12);
        graph.addEdge(11,12);
        //深度优先搜索对象
        DepthFirstSearch search = new DepthFirstSearch(graph, 0);
        System.out.println();
        System.out.println(search.count());
        //测试某个顶点与起点是否相同
        System.out.println(search.marked(7));
        System.out.println(search.marked(5));
    }
}

BFS

package com.example.demo.code60;

import com.example.demo.code10.queue.Queue;

import java.util.LinkedList;

/**
 * @author ming
 * @create 2022/6/10
 * @description:
 */
public class BreadFirstSearch {
    //标记顶底是否已经被搜素
    private boolean [] marked;
    private int count;
    private Queue<Integer> waitSearch;
    public BreadFirstSearch(Graph g,int s ) {
        this.marked = new boolean[g.v()];
        this.count = 0;
        this.waitSearch = new Queue<Integer>();
        bfs(g,s);
    }

    private void bfs(Graph g, int s) {
       marked[s] = true;
       waitSearch.enqueue(s);
       while (!waitSearch.isEmpty()) {
           Integer wait = waitSearch.dequeue();
           Queue<Integer> adj = g.adj(wait);
           for (Integer w : adj) {
               if(!marked[w]) {
                   waitSearch.enqueue(w);
                   marked[w] = true;
                   count++;
                   System.out.print(w+" ");
               }

           }
       }
    }

    public static void main(String[] args) {
        //创建图
        Graph graph = new Graph(13);
        graph.addEdge(0,5);
        graph.addEdge(0,1);
        graph.addEdge(0,2);
        graph.addEdge(0,6);
        graph.addEdge(5,3);
        graph.addEdge(5,4);
        graph.addEdge(3,4);
        graph.addEdge(4,6);
        graph.addEdge(7,8);
        graph.addEdge(9,11);
        graph.addEdge(9,10);
        graph.addEdge(9,12);
        graph.addEdge(11,12);
        //广度优先搜索对象
       BreadFirstSearch search = new BreadFirstSearch(graph,0);




    }
    
}