零维内弹道方程龙格库塔法

​​​​

固体火箭内弹道学方程可以简画出曲线图我便以固体火箭发动机内弹道学的零维内弹道方程龙格库塔法进行最简单的陈述。首先我先声明一下，本帖有编程计算和手动计算两种形式，让我们先了一解一下零维内弹道方程：零维内弹道方程描述燃烧室内压力随时间变化，忽略空间分布，仅考虑时间变量。常用于分析火箭发动机或火炮的内弹道过程，通过燃烧释放热量和气体膨胀计算压力变化。再介绍一下龙格库塔法：龙格法（龙格-库塔法）是一种数值求解微分方程的方法，通过多步加权计算提高精度，尤其四阶龙格-库塔法广泛用于科学计算和工程仿真。


第一步：零维内弹道方程的主要构成。
零维内弹道方程是描述燃烧室内压力随时间变化的数学模型，通常用于分析火箭发动机或火炮的内弹道过程。龙格-库塔法（Runge-Kutta method）是一种数值求解微分方程的方法，适用于求解零维内弹道方程。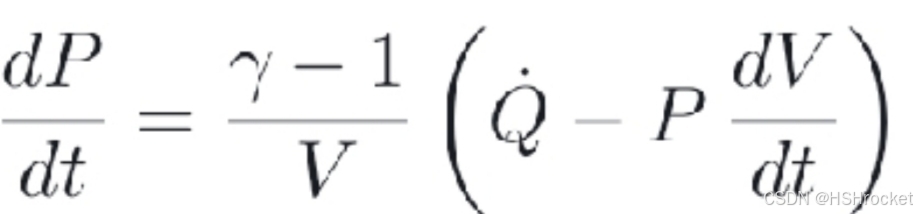

• P是燃烧室压力

• t是时间

• Y是比热比

• V是燃烧室体积

如果将V设为常数，便可简化式子为：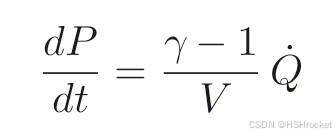

第二步：龙格库塔法
零维内弹道方程是描述燃烧室内压力随时间变化的数学模型，通常用于分析火箭发动机或火炮的内弹道过程。龙格-库塔法（Runge-Kutta method）是一种数值求解微分方程的方法，适用于求解零维内弹道方程。龙格-库塔法是一种数值积分方法，用于求解微分方程。对于方程：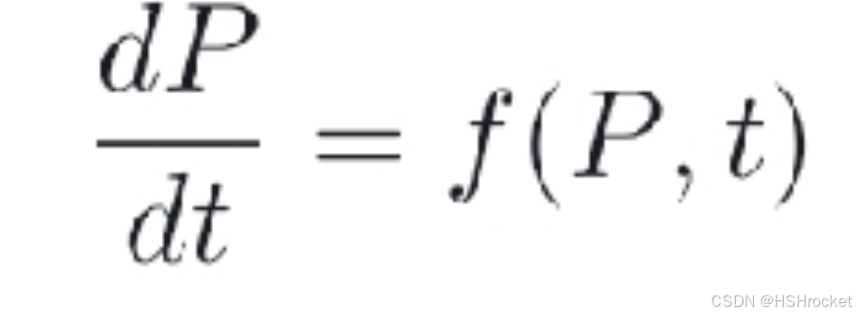

四阶龙格-库塔法的迭代公式为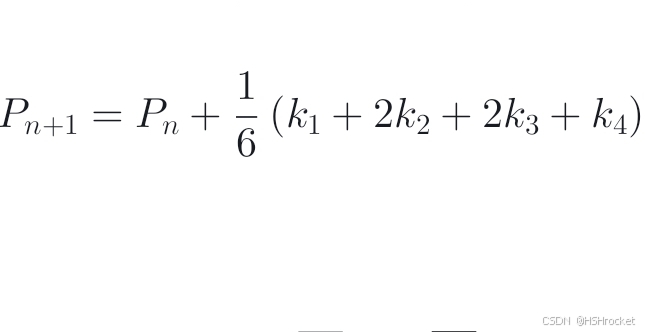

其中：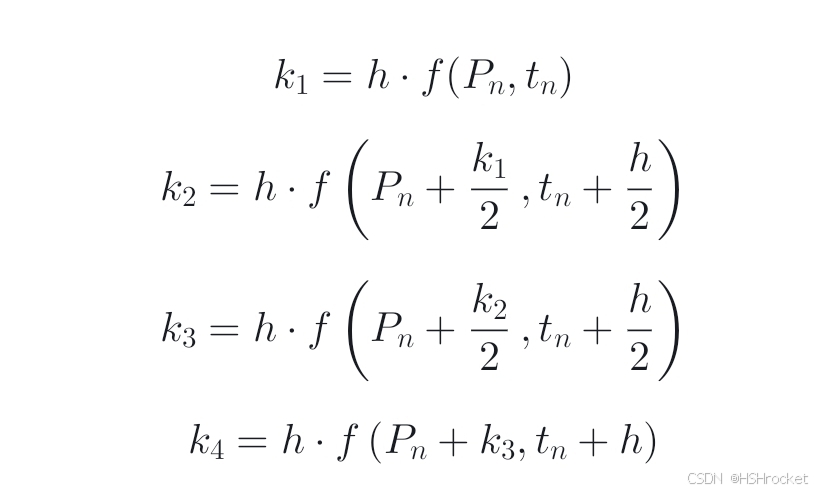

第三步：手绘气压随时间变化曲线
1. 初始化参数
   - 初始压力
   - 时间步长
   - 总时间
   - 燃烧释放的热量速率
   - 燃烧室体积
   - 比热比
2、迭代计算
3、绘图

第四步：编程代码
如下：

Python

开启自动换行复制

import numpy as np import matplotlib.pyplot as plt # 定义零维内弹道方程 def dPdt(P, t, gamma, V, Q_dot): return (gamma - 1) / V * Q_dot # 四阶龙格-库塔法 def runge_kutta_4th_order(P0, t, h, gamma, V, Q_dot): P = np.zeros(len(t)) P[0] = P0 for i in range(1, len(t)): k1 = h * dPdt(P[i-1], t[i-1], gamma, V, Q_dot) k2 = h * dPdt(P[i-1] + 0.5 * k1, t[i-1] + 0.5 * h, gamma, V, Q_dot) k3 = h * dPdt(P[i-1] + 0.5 * k2, t[i-1] + 0.5 * h, gamma, V, Q_dot) k4 = h * dPdt(P[i-1] + k3, t[i-1] + h, gamma, V, Q_dot) P = P[i-1] + (k1 + 2*k2 + 2*k3 + k4) / 6 return P # 参数设置 P0 = 0.0 # 初始压力 (Pa) gamma = 1.4 # 比热比 V = 1.0 # 燃烧室体积 (m³) Q_dot = 1000 # 燃烧释放热量速率 (J/s) t_end = 10 # 总时间 (s) h = 0.1 # 时间步长 (s) # 时间数组 t = np.arange(0, t_end + h, h) # 计算压力随时间变化 P = runge_kutta_4th_order(P0, t, h, gamma, V, Q_dot) # 绘制气压随时间变化曲线 plt.plot(t, P, label="Pressure (Pa)") plt.xlabel("Time (s)") plt.ylabel("Pressure (Pa)") plt.title("Pressure vs Time in Zero-Dimensional Interior Ballistics") plt.grid() plt.legend() plt.show(）

第五步：实例

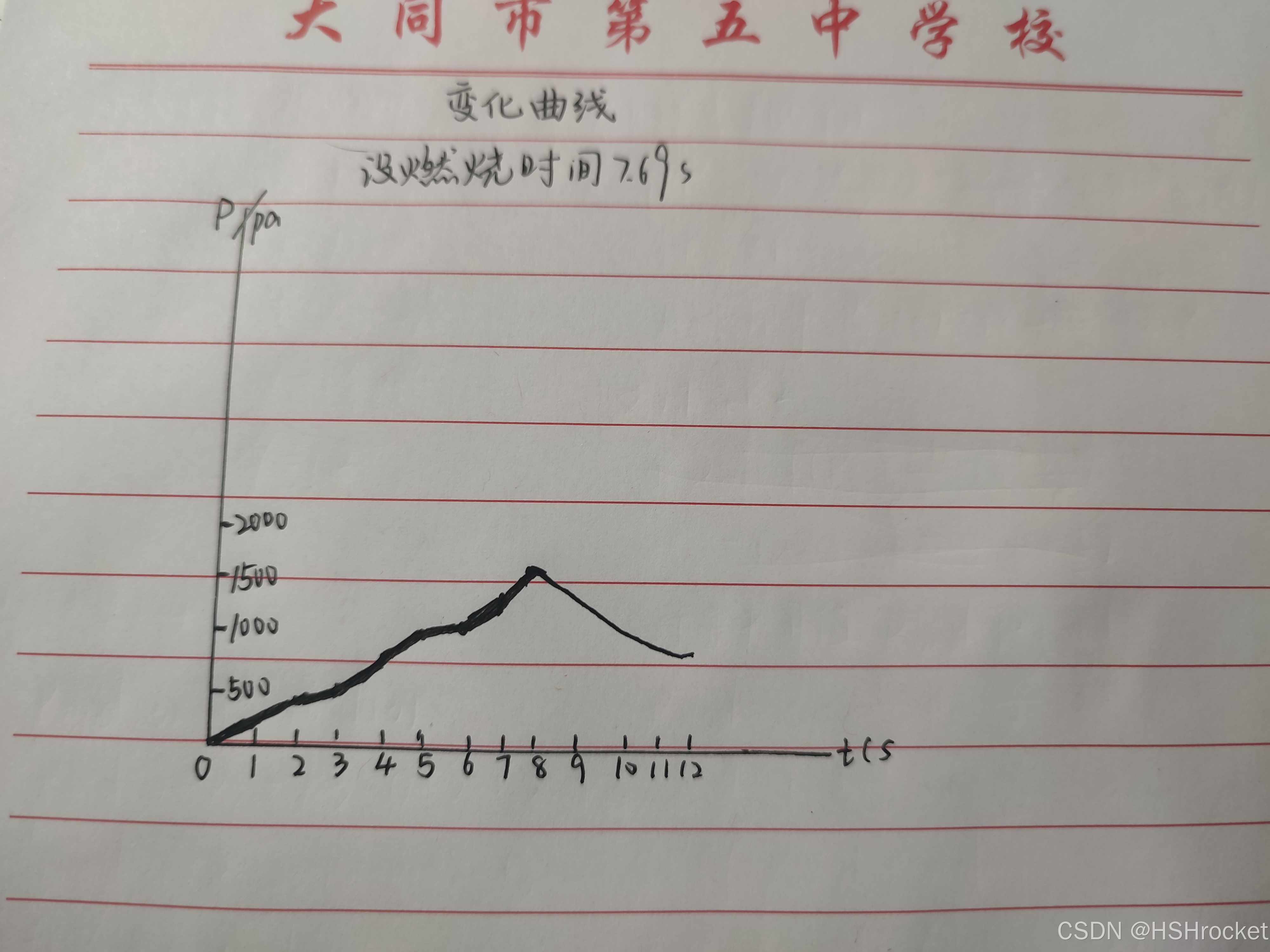
第七步：燃烧时间曲线结合计算法

手算方式

代码

Python

开启自动换行复制

import numpy as np import matplotlib.pyplot as plt # 参数设置 d = 88e-3 # 装药内径 (m) D = 106e-3 # 装药外径 (m) L = 200e-3 # 装药长度 (m) rho_p = 1775 # 装药密度 (kg/m^3) V_c = 0.0079 # 燃烧室初始自由容积 (m^3) r_gas = 1.2 # 燃气比热比 c_star = 1500 # 燃气特征速度 (m/s) d_t = 17e-3 # 喷喉直径 (m) p_c_t = 1.5e6 # 点火压强 (Pa) p_a = 0.098e6 # 环境压强 (Pa) T_c = 3260 # 燃烧温度 (K) burn_rate_coeff = 8.3e-5 # 燃速系数 burn_rate_exp = 0.3 # 燃速指数 # 计算装药燃烧厚度 e = (D - d) / 2 # 燃速公式 def burn_rate(p_c): return burn_rate_coeff * p_c ** burn_rate_exp # 燃烧时间计算 def burn_time(p_c): return e / burn_rate(p_c) # 零维内弹道方程 def dpcdt(p_c, t): if t <= burn_time(p_c): # 燃烧阶段 m_dot_p = burn_rate(p_c) * rho_p * np.pi * (D**2 - d**2) / 4 * L else: # 燃烧结束，停止产生燃气 m_dot_p = 0 A_t = np.pi * (d_t / 2)**2 # 喷喉面积 m_dot_g = p_c * A_t / (c_star * np.sqrt(T_c)) # 喷喉质量流量 return (r_gas - 1) / V_c * (m_dot_p - m_dot_g) # 四阶龙格-库塔法 def runge_kutta_4th_order(p_c0, t, h): p_c = np.zeros(len(t)) p_c[0] = p_c0 for i in range(1, len(t)): k1 = h * dpcdt(p_c[i-1], t[i-1]) k2 = h * dpcdt(p_c[i-1] + 0.5 * k1, t[i-1] + 0.5 * h) k3 = h * dpcdt(p_c[i-1] + 0.5 * k2, t[i-1] + 0.5 * h) k4 = h * dpcdt(p_c[i-1] + k3, t[i-1] + h) p_c = p_c[i-1] + (k1 + 2*k2 + 2*k3 + k4) / 6 return p_c # 时间数组 t_end = 20 # 总时间 (s)，确保覆盖燃烧和排气阶段 h = 0.01 # 时间步长 (s) t = np.arange(0, t_end, h) # 计算燃烧室压强随时间变化 p_c = runge_kutta_4th_order(p_c_t, t, h) # 绘制燃烧室压强随时间变化曲线 plt.plot(t, p_c / 1e6, label="Chamber Pressure (MPa)") plt.xlabel("Time (s)") plt.ylabel("Pressure (MPa)") plt.title("Chamber Pressure vs Time") plt.grid()

见谅，望对大家有用