转载自——隐马尔可夫模型 - HMM的三个问题 - 预测问题 - Viterbi算法
原文中的有些过程不是很详细,我在这里进行了修改!并且添加了代码实现部分
目录
问题: 在观测序列已知的情况下,状态序列未知。想找到一个最有可能产生当前观测序列的状态序列。
可以用下面两种办法来求解这个问题:
1、近似算法
2、Viterbi算法
近似算法
直接在每个时刻t时候最优可能的状态作为最终的预测状态,使用下列公式计算概率值:
遍历时间t。
优点是计算简单;而缺点就很明显了,没有考虑时序关系,不能保证预测的状态序列整体上是最优可能的状态序列,预测的状态序列可能有实际不发生的部分。
Viterbi算法
它的核心思想和运筹学中的使用动态规划的思路求解最短路径问题是一样的。
其中it表示最短路径,Ot表示观测符号,lamda表示模型参数,根据上式可以得出变量sigma的递推公式:

下面看个例子来深入理解这个公式。
HMM案例-Viterbi
在给定参数π、A、B的时候,得到观测序列为“白黑白白黑”,求出最优的隐藏状态序列。

回溯最优路径:

最优状态序列为:23223
代码实现
这里把最原始的viterbi算法做一个简单的实现——代码来自github——viterbi
###########################################################################################################
# Viterbi Algorithm for HMM
# dp, time complexity O(mn^2), m is the length of sequence of observation, n is the number of hidden states
##########################################################################################################
# five elements for HMM
states = ('1号盒子', '2号盒子','3号盒子')
observations = ('白球', '黑球', '白球','白球','黑球')
start_probability = {'1号盒子': 0.2, '2号盒子': 0.5,'3号盒子':0.3}
transition_probability = {
'1号盒子': {'1号盒子': 0.5, '2号盒子': 0.4,'3号盒子':0.1},
'2号盒子': {'1号盒子': 0.2, '2号盒子': 0.2,'3号盒子':0.6},
'3号盒子': {'1号盒子': 0.2, '2号盒子': 0.5,'3号盒子':0.3}
}
emission_probability = {
'1号盒子': {'白球': 0.4, '黑球': 0.6},
'2号盒子': {'白球': 0.8, '黑球': 0.2},
'3号盒子': {'白球': 0.5, '黑球': 0.5}
}
def Viterbit(obs, states, s_pro, t_pro, e_pro):
path = {s: [] for s in states} # init path: path[s] represents the path ends with s
curr_pro = {}
for s in states:
curr_pro[s] = s_pro[s] * e_pro[s][obs[0]]
for i in range(1, len(obs)):
last_pro = curr_pro
curr_pro = {}
for curr_state in states:
max_pro, last_sta = max(
((last_pro[last_state] * t_pro[last_state][curr_state] * e_pro[curr_state][obs[i]], last_state)
for last_state in states))
curr_pro[curr_state] = max_pro
path[curr_state].append(last_sta)
# find the final largest probability
max_pro = -1
max_path = None
for s in states:
path[s].append(s)
if curr_pro[s] > max_pro:
max_path = path[s]
max_pro = curr_pro[s]
# print '%s: %s'%(curr_pro[s], path[s]) # different path and their probability
return max_path
if __name__ == '__main__':
obs = ['白球', '黑球', '白球','白球','黑球']
print(Viterbit(obs, states, start_probability, transition_probability, emission_probability))代码原理很好理解,主要是要把不同时刻的最优路径的当前状态和前一时刻的状态都保存下来,然后再回溯全局最优路径。代码不熟悉的话可以多调试一下!








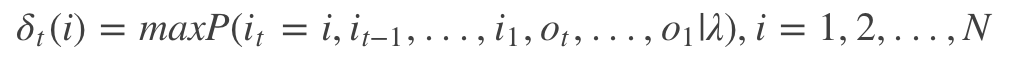
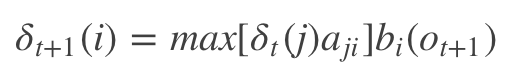













 4768
4768











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








