（翻译+部分总结）莫队算法入门小结

最近入门了莫队算法，觉得好玄妙，为自己写个小结。

我初学莫队算法是通过这个博客理解的：戳这里，只不过是英文的，其他人也写过这篇博文的翻译，特此注明。
下面我的小结也主要围绕这个问题来谈。
考虑这个问题：
给定一个序列{$a_n$}，共有m次询问，每次询问区间{l,r}中出现次数大于等于3的数字有多少个。
我们先来考虑n,m较小的情况。
暴力统计可以解决，用$cnt[n]$表示n在该子序列中的数量，直接统计答案。

int solve(int l,int r)
{
    memset(cnt,0,sizeof(cnt));
    int rtn=0;
    for(int i=l;i<=r;i++)
    {
        cnt[a[i]]++;
        if(cnt[a[i]]==3)rtn++;
    }
    return rtn;
} 

这个样子做，复杂度看得出来，最坏情况下（每次查询整个区间）是$O(nm)$的。
我们得想办法优化一下。
…………
…………
…………
由于我们并没有涉及到修改操作，所以每一个$a[i]$对答案的贡献一定是固定的，因而我们在多次查询中，会重复统计许多$a[i]$对答案的贡献。事实上，上一个查询的区间如果与下一个查询的区间有交集（甚至重合）的话，我们是完全没有必要再统计一遍他们公共部分的答案的！
看下面这段代码：

int n,m;
int cnt[100010],a[100010];
int ans[100010],now_ans;//now_ans:当前答案 ans[i]:第[i]次询问的答案
struct query{
    int l,r;
}q[100010];//记录每个查询的信息
void del(int pos){//删除a[pos]对答案的贡献
    cnt[a[pos]]--;
    if(cnt[a[pos]]==2)now_ans--;
    //如果此时cnt[a[pos]]=2，那么在减之前它就等于3，对答案有贡献
}

void inc(int pos){//计算a[pos]对答案的贡献
    cnt[a[pos]]++;
    if(cnt[a[pos]]==3)now_ans++;
}

void solve(){
    int now_l=1,now_r=1;//记录上一个询问的左、右端点
    for(int i=1;i<=m;i++){//统计所有询问
        int ll=q[i].l,rr=q[i].r;
        while(now_l>ll){
            inc(now_l-1);now_l--;
        }
        while(now_r<=rr){
            inc(now_r);now_r++;
        }
        while(now_l<ll){
            del(now_l);now_l++;
        }
        while(now_r>rr+1){
            del(now_r-1);now_r--;
        }
        ans[i]=now_ans;
    }
}

噫！一下子变得这么长了！还套进了四个while循环和两个函数！
不要急不要急，如果你能理解这段代码，那就是学会了半个莫队算法呢！
首先看到solve函数：
这段代码的核心思想是只修改上一个区间与当前区间的不同位置，因此我们需要从记录的上一个区间的两个顶点出发（now_l和now_r），移动到当前查询的区间两端点，沿途修改答案。
那么那么为什么是这样移动的呢？
那么那么为什么还要+1-1什么的呢？
别急……
对于左端点而言，它到右端点的这一区间是已经统计过了的。那么如果它还要往右移动，就必然会经过已统计过答案的区间！那么这就使原来统计过的部分留在了左端点左边（也就是说，不在我的下一个统计区间了），因此，左端点要向右移动的话，沿途的部分对答案的贡献需要被删除。与此同时，如果向左移动，左端点左边的区间必然不在我的原区间内，所以向左移动，需要增加它对答案的贡献。
右端点也是可以类比的。
至于加一减一，大于等于的问题，我们可以画出上个区间与下个区间关系的不同情况，自己按照算法推演一下，也就不难理解了。（其实是我不会QAQ）
……
……
……
请仔细理解上面的代码，然后再往下看。
我们还是不难发现，这个代码的复杂度，取决于now_l和now_r的移动次数，最坏情况下，每次查询，都要从头已到尾，就依然是个$O(nm)$的算法，本质上没什么提高。
说好的优化呢？？？
别急……
既然复杂度取决于两端点的移动，那么……
我们合理安排一下查询的顺序，让两端点科学有效地运动，不就好了吗？
怎么排序呢……
now_l：按我排序，按左端点从小到大排序！我最多只从左到右走一遍！
now_r: →_→那我呢……我每次不是就只能瞎跑了……你倒好只跑一遍，我每查一次都恨不得要跑一趟ToT
now_l：(⊙o⊙)…那怎么办……
now_r：你看啊，按你排序，我每次的复杂度就是$O(n)$，按我排序，你的复杂度就是$O(n)$，所以啊……我们可以委曲求全……搞个$O(\sqrt n)$出来。
now_l ：蛤？我们妥协是怎么妥协出$O(\sqrt n)$来的？
now_r ：→_→你没学过分块吗……
now_l ：我只是个端点而已……
now_r ：……
我们将1-n分成$O(\sqrt n)$个块，每个块内大致就有$O(\sqrt n)$个元素，每个元素也就有自己对应的块编号。对于所有的询问，我们找到左端点，按照它所在块的编号排序。
now_l：那有好多查询的块编号一样的呢！（now_r：闭嘴！）
对于块编号相等的询问，我们就按照右端点的升序排列。
例如对于如下询问：
{1, 3} {1, 7} {2, 8} {7, 8} {4, 8} {4, 4} {1, 2}
我们先按照块编号排序：
{1, 3} {1, 7} {2, 8} {1, 2} {4, 8} {4, 4} {7, 8}
再对同一块内的查询按右端点升序排序：
{1, 2} {1, 3} {1, 7} {2, 8} {4, 4} {4, 8} {7, 8}
按照这个顺序处理所有询问。
现在，我们就面临莫队算法的最后一个问题：
复杂度？
我们来这么看：
对于右端点而言，在每个块中，由于按照升序排列，所以最多移动n次，由于总共有n√个块，所以右端点最多移动$n\sqrt n$次。（或者说是$n^\frac {3}{2}$）
对于左端点而言，每次询问的移动虽然不确定，但是由于我把同一个块的元素排在了一起，所以每次查询，都相当于在块内移动，因而最大幅度为$m\sqrt n$次。
综上，莫队算法的复杂度为$O((n+m)\sqrt n)$即$O(n\sqrt n)$（或$O(n^\frac {3}{2})$)。
到此，莫队算法的基本概念介绍完毕。
这是解决这个问题的最终代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
int n,m,num;
int cnt[100010],a[100010];
int ans[100010],now_ans;//now_ans:当前答案 ans[i]:第[i]次询问的答案
struct query{
    int l,r,id;//id:记录这个查询是第几个查询，以便最后输出答案 
}q[100010];//记录每个查询的信息

int cmp(query x,query y){//比较函数 
    int p_x=(x.l-1)/num+1,p_y=(y.l-1)/num+1;//计算左端点所属块编号 
    if(p_x==p_y)return x.r<y.r;//若块编号相同，则按右端点升序排列 
    else return p_x<p_y;
}

void del(int pos){//删除a[pos]对答案的贡献
    cnt[a[pos]]--;
    if(cnt[a[pos]]==2)now_ans--;
    //如果此时cnt[a[pos]]=2，那么在减之前它就等于3，对答案有贡献
}

void inc(int pos){//计算a[pos]对答案的贡献
    cnt[a[pos]]++;
    if(cnt[a[pos]]==3)now_ans++;
}

void solve(){
    int now_l=1,now_r=1;//记录上一个询问的左、右端点
    for(int i=1;i<=m;i++){//统计所有询问
        int ll=q[i].l,rr=q[i].r;
        while(now_l>ll){
            inc(now_l-1);now_l--;
        }
        while(now_r<=rr){
            inc(now_r);now_r++;
        }
        while(now_l<ll){
            del(now_l);now_l++;
        }
        while(now_r>rr+1){
            del(now_r-1);now_r--;
        }
        ans[q[i].id]=now_ans;//q[i]实际上是第q[i].id次询问 
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    num=(int)sqrt(n);//块的大小 
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&q[i].l,&q[i].r);
        q[i].id=i;
    }
    sort(q+1,q+1+m,cmp);//排序
    solve();
    for(int i=1;i<=m;i++)printf("%d\n",ans[i]) ;
    return 0;
}  

神奇的莫队算法，只通过排序就可以将$O(nm)$的算法重置为$O(n\sqrt n)$，但是，它还是有一些缺陷，主要如下:
1.莫队算法是一种离线算法，所以如果题目要求强制在线，那就没辙了。
2.由于莫队算法通过不断添加/删除某位置对答案的贡献，所以就要求相应的修改操作（如本题中的inc和del函数）不能太复杂。某些情况下我们的修改操作可能就不会像本题一样能在$O(1)$内完成，有可能是$O(\log n)$甚至是$O(\sqrt n)$，无形中加大了复杂度。
3.在$10^5$的范围内，莫队算法的表现很不错，甚至可以与一些$O(\log n)$的算法相近，但是数据规模上到$10^6$的话，莫队算法的表现就够呛了。比如CF 703D这道题，相关的操作非常适合莫队，但是由于数据范围达到$10^6$，尽管时限达到3.5s，但是不加快速读入输出以及其他优化的话，很容易得TLE。
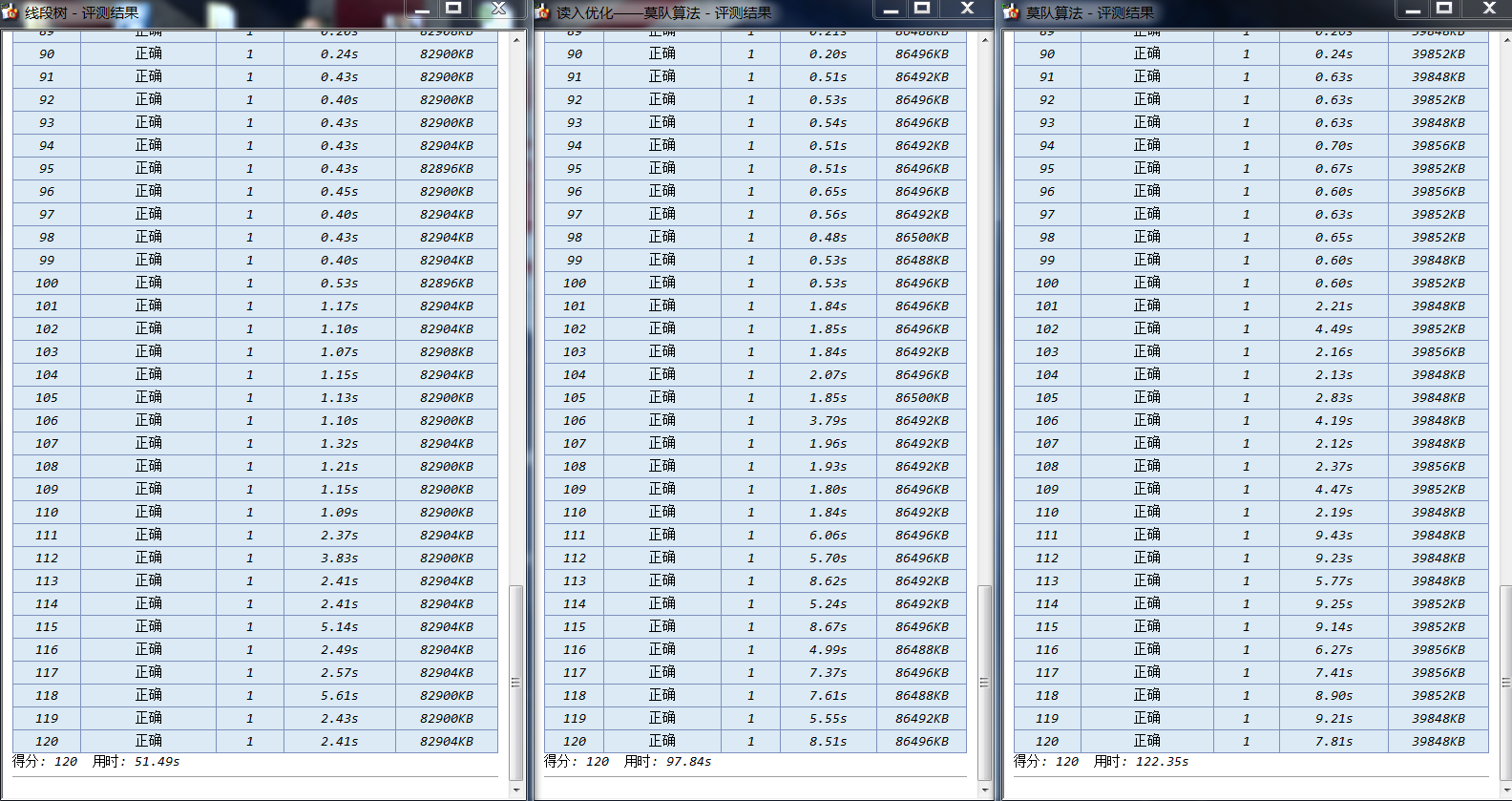
下面就是我用cena测试的结果：
90以内的数据都在$10^5$以内，91-100规模为200000，101-110为500000,111-120为1000000.

2016.08.27 未完待续