平衡二叉查找树（JAVA）

之前我分享过二叉查找树（也叫二叉排序树）的BST博客

二叉排序树 与 平衡二叉排序树

俩者官方定义

二叉排序树定义就是（1）任何节点的左节点值都比当前根节点值小。（2）所有右节点值都比当前根节点值大。 （3）且所有子树也都是二叉排序树。

平衡二叉排序树定义(1)首先整体为二叉查找树。(2)左子树与右子树的深度之差的绝对值小于或等于1。 (3),左右子树也是平衡二叉查找树。

我们有了二叉排序树为什么我们还需要平衡二叉排序树？

大家都知道树的结构其实也算是链表的一种变形，所以在最坏情况下树有可能变成线性的链表，那么此时遍历的效率（平均查找长度）很比较差（长），也失去了树的结构定义的初衷。
所以平衡二叉排序树就是为了维护“树”的基本形态。

平衡二叉排序树

平衡因子

平衡因子存储在节点当中，其含义就是当前节点的左子树深度与右子树深度之差。
如果一棵树所有节点的平很因子都是（0，1，-1），那么此树就为平衡二叉排序树。

其中的特殊点

A节点：为插入点顶层“祖先节点”中最大可能的失衡点（提醒一下最可能的往往是平衡因子不为0的节点，之后程序示例中会体现出来）。如果没有找到，说明插入这个节点不可能破坏平衡
B节点：就是该祖先节点一条线中A节点的下一个。
C节点：这个节点有可能用上也有可能没用，当非平衡树的状态类型为LR或者RL型时，C节点就是B节点的子节点（左右根据大小来放置）。其它类型C节点无用处。

四个非平衡状态时的转换类型

图片来自博客一个技术人员的草稿纸，侵删
（1）LL型

（2）RR型

（3）LR型

（4）RL型 与（3）同理

平衡二叉排序树代码实现

class TreeNode {
    int value;
    int bf; //平衡因子
    TreeNode left_node;
    TreeNode right_node;
    public TreeNode(int value, int bf) {
        this.bf = bf;
        this.value = value;
        this.left_node = null;
        this.right_node = null;
    }
}

public class BalanceBinaryTree {
    private final int LL = 1;
    private final int RR = 2;
    private final int LR = 3;
    private final int RL = 4;
    private TreeNode RootNode;

    public void insert(int value) {
        int choice = 0;
        TreeNode A = RootNode;
        TreeNode B = null;
        TreeNode C = null;
        TreeNode Father_A = null;
        TreeNode HelpNode = null;
        TreeNode CurrentNode = RootNode;

        //创建要插入的节点
        TreeNode node = new TreeNode(value, 0);
        //如果一开始根节点为空，直接将当前值设置为根节点
        if(RootNode == null) {
            RootNode = node;
            return;
        }
        //找到要插入的节点，并且找到最可能失去平衡点的节点A，Father_A为A的父节点
        while (CurrentNode != null) {
            if(CurrentNode.bf !=0 ) {
                A = CurrentNode;
                Father_A = HelpNode;
            }
            HelpNode = CurrentNode;
            if(CurrentNode.value < value) {
                CurrentNode = CurrentNode.right_node;
            }
            else {
                CurrentNode = CurrentNode.left_node;
            }
        }

        //插入目标节点
        if(HelpNode.value < value) {
            HelpNode.right_node = node;
        }
        else {
            HelpNode.left_node = node;
        }

        //确定B节点，并修改A的平衡因子bf
        if(value < A.value) {
            B = A.left_node;
            A.bf = A.bf + 1;
        } else {
            B = A.right_node;
            A.bf = A.bf - 1;
        }

        //修改其它节点的平衡因子bf
        CurrentNode = B;
        while (CurrentNode != node) {
            if(value < CurrentNode.value) {
                CurrentNode.bf = 1;
                CurrentNode = CurrentNode.left_node;
            } else {
                CurrentNode.bf = -1;
                CurrentNode = CurrentNode.right_node;
            }
        }

        if(A.bf == 2 && B.bf == 1) {
            choice = LL;
        }
        else if(A.bf == -2 && B.bf == -1) {
            choice = RR;
        }
        else if(A.bf == 2 && B.bf == -1) {
            choice = LR;
        }
        else if(A.bf == -2 && B.bf == 1) {
            choice = RL;
        }
        else {
            choice = 0;
        }

        switch (choice) {
            case LL:
                B = A.left_node;
                A.left_node = B.right_node;
                B.right_node = A;
                A.bf = B.bf = 0;
                if(Father_A == null) {
                    RootNode = B;
                }
                else if (A == Father_A.left_node) {
                    Father_A.left_node = B;
                }
                else {
                    Father_A.left_node = B;
                }
                break;
            case LR:
                B = A.left_node;
                C = B.right_node;
                B.right_node = C.left_node;
                A.left_node = C.right_node;
                C.left_node = B;
                C.right_node = A;
                if(node.value < C.value) {
                    A.bf = -1;
                    B.bf = 0;
                    C.bf = 0;
                }
                else if(node.value > C.value) {
                    A.bf = 0;
                    B.bf = 1;
                    C.bf = 0;
                }
                else {
                    A.bf = 0;
                    B.bf = 0;
                }
                if(Father_A == null) RootNode = C;
                else if(A == Father_A.left_node) {
                    Father_A.left_node = C;
                }
                else {
                    Father_A.right_node = C;
                }
                break;
            case RL:
                B = A.right_node;
                C = B.left_node;
                B.left_node = C.right_node;
                A.right_node = C.left_node;
                C.left_node = A;
                C.right_node = B;
                if(node.value < C.value) {
                    A.bf = 0;
                    B.bf = -1;
                    C.bf = 0;
                }
                else if(node.value > C.value) {
                    A.bf = 1;
                    B.bf = 0;
                    C.bf = 0;
                }
                else {
                    A.bf = 0;
                    B.bf = 0;
                }
                if(Father_A == null) RootNode = C;
                else if(A == Father_A.left_node) {
                    Father_A.left_node = C;
                }
                else {
                    Father_A.right_node = C;
                }
                break;
            case RR:
                B = A.right_node;
                A.right_node = B.left_node;
                B.left_node = A;
                A.bf = B.bf = 0;
                if(Father_A == null) RootNode = B;
                else if(A==Father_A.left_node) {
                    Father_A.left_node = B;
                }
                else {
                    Father_A.right_node = B;
                }
                break;
            default:
                System.out.println("插入一个节点时没有破坏原有的平衡状态");
                break;
        }

        return ;
    }

    private void FirstOrder(TreeNode node) {
        if(node != null) {
            System.out.print(node.value + " ");
            FirstOrder(node.left_node);
            FirstOrder(node.right_node);
        }
    }

    private void InOrder(TreeNode node) {
        if(node != null) {
            FirstOrder(node.left_node);
            System.out.print(node.value + " ");
            FirstOrder(node.right_node);
        }
    }

    private void PostOrder(TreeNode node) {
        if(node != null) {
            PostOrder(node.right_node);
            System.out.print(node.value + " ");
            PostOrder(node.left_node);
        }
    }

    //搜索节点
    private TreeNode Search(TreeNode rootNode, int value) {
        while (rootNode != null) {
            if(rootNode.value == value) {
                return rootNode;
            }
            else if(rootNode.value > value) {
                rootNode = rootNode.left_node;
            }
            else {
                rootNode = rootNode.right_node;
            }
        }
        return null;
    }

    public static void main(String[] args) {
        BalanceBinaryTree balanceBinaryTree = new BalanceBinaryTree();
        balanceBinaryTree.insert(20);
        balanceBinaryTree.insert(30);
        balanceBinaryTree.insert(25);
        balanceBinaryTree.insert(40);
        balanceBinaryTree.insert(60);
        System.out.print("先序遍历：");
        balanceBinaryTree.FirstOrder(balanceBinaryTree.RootNode);
        System.out.println();
        System.out.print("中序遍历：");
        balanceBinaryTree.InOrder(balanceBinaryTree.RootNode);
        System.out.println();
        System.out.print("后序遍历：");
        balanceBinaryTree.PostOrder(balanceBinaryTree.RootNode);
        System.out.println();
    }
}

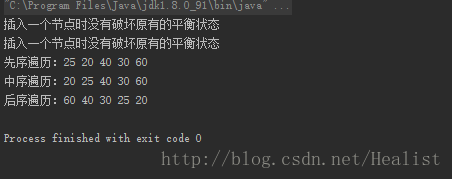
示例代码运行结果：