算法：树状数组

树状数组解决的两个问题：

1. 快速求前缀和 O(log₂n)
2. 修改某一个数 O(log₂n)

上面两个操作分别用可以实现相应的做法

1. 前缀和 O(n) O(1)
2. 数组 O(n) O(1)

树状数组折中

算法原理基于二进制算法：

• 每一个数可以被分为最多log(x)个部分
  
  可以使得我们在log(n)的时间复杂度之内，求出前n项的前缀和，分析一个上面每个区间分别由几个数（绿字）：
  
  再观察每个区间右端点和区间长度的关系：
  
  假设一个左开右闭区间（L , R]，其区间长度一定是R的二进制表示的最后一位1，所对应的次幂：即lowbit(x)，换成闭区间要加1：
  
  我们用C[R]来表示：
  
  用C[x]来表示：该区间所有树的和
  

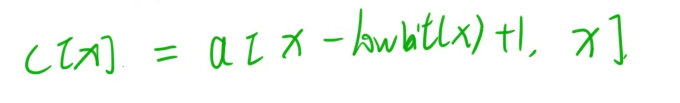
画图表示分别以x = 1 ~ 16结尾的长度是lowbit(x)的区间

C[16] = A[16] + C[15] + C[14] + C[12] + C[8];
用后面的Tr[i]表示
就是Tr[i] = A[i] + Tr[i - 1] + Tr[i - 1 - lowbit(i - 1)] + Tr[i - 1 - lowbit(i - 1) - lowbit(i - 1 - lowbit(i - 1))] + …
这里
i = 16 , i - 1 = 15, i - 1 - lowbit(i - 1) = 14, 对应14 - lowbit(14) = 12; 12 -lowbit(12) = 8;

以此类推所由不同C的关系

代码验证：假设一个数组_nums[8] = {1,2,3,4,5,6,7,8};
每次开始时先写以下三个函数：

初始化：

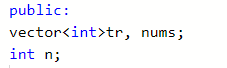
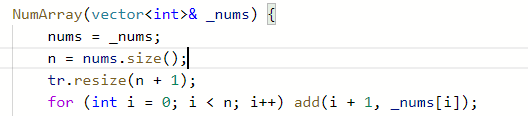
得到tr[]数组的过程以及最终tr为：

i = 1, tr[1] = 1
i = 2, tr[2] = 1
i = 4, tr[4] = 1
i = 8, tr[8] = 1

i = 2, tr[2] = 3
i = 4, tr[4] = 3
i = 8, tr[8] = 3

i = 3, tr[3] = 3
i = 4, tr[4] = 6
i = 8, tr[8] = 6

i = 4, tr[4] = 10
i = 8, tr[8] = 10

i = 5, tr[5] = 5
i = 6, tr[6] = 5
i = 8, tr[8] = 15

i = 6, tr[6] = 11
i = 8, tr[8] = 21

i = 7, tr[7] = 7
i = 8, tr[8] = 28

i = 8, tr[8] = 36

tr[1] = 1 tr[2] = 3 tr[3] = 3 tr[4] = 10 tr[5] = 5 tr[6] = 11 tr[7] = 7 tr[8] = 36

和上图对照看，求区间和时的公式


注意这里query传给tr数组，其下标为[1,n],sumRange传的是原数组num的小标i,j，范围是[0,n-1]，所以这里假设要求nums [0,7]的区间和，就是求前缀和（下标加一）sum[8] - sum[0], 而sum[8]就是根据tr[8] + tr[8 - lowbit(8)] + … 这里正好8 - lowbit(8)就是0，所以sum[8]就是tr[8]，但是这只是一个巧合，假设是求nums下标为[2,10]的区间和，就是sum[11]- sum[2]，这里的sum[11]，sum[11] = tr[11] + tr[10] + tr[8]…

回过来对于 nums[0,7] 就是query(8) - query(0), query(8)只会加一个 tr[8] = 36，因为减去lowbit(8)就变成0，

假设求nums[2, 6], 就是求原区间下标[2,6]的和 对应了下标加一的sum 为 sum[7] - sum[2], 即query(7) - query(2), 在query(7) 里求sum[7]的过程为

• res = tr[7] + tr[6] + tr[4]

验证入下：

x为：7
i = 7, tr[7] = 7, res = 7
i = 6, tr[6] = 11, res = 18
i = 4, tr[4] = 10, res = 28

7 (111)₂ 被分为三个区间 ，每个区间长度为lowbit®

(110, 111] 十进制(6,7]
(100，110] 十进制(4,6]
(000,100] 十进制 (0,4]

至此验证完毕，对于单点更新或者查询和来说树状数组可以在log_n的时间内完成，对Q个数插入add的时间复杂度为O(Qlogn),初始化时若用定义初始化tr数组可以控制时间复杂度为O(n) 总时间复杂度为 O(n + Qlogn)

以下为初始化时间复杂度为O(nlogn)以及O(n)的两种写法

//O(nlog(n))插入
        // for (int i = 0; i < n; i++) add(i + 1, _nums[i]);
        //O(n)插入,用到定义， 第二层循环会在常数个时间内解决
        for (int i = 1; i <= n; i ++ ) {
            tr[i] = nums[i - 1]; //  Tr[i] = A[i] + Tr[i - 1] + Tr[i - 1 - lowbit(i - 1) ... ] ，外部的Tr[i]是从1开始的所以比nums[]多加了一个
            for (int j = i - 1; j > i - lowbit(i); j -= lowbit(j))
                tr[i] += tr[j];
        }
————————————————
版权声明：本文为CSDN博主「肖源杰」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Heck_Jacke/article/details/123654590

假设一个x：

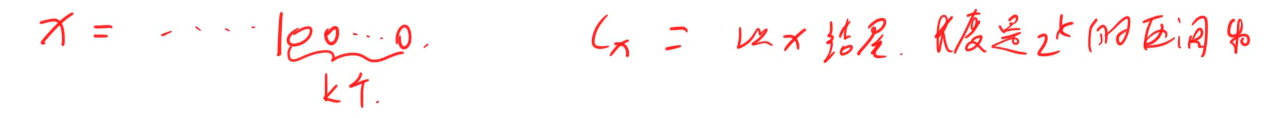
C[x]就等于 自己这个数A[x]，加上前面的C[]:

x -1 最后的k个1由可以拆分成以下几个儿子，（以下的左开右闭区间）

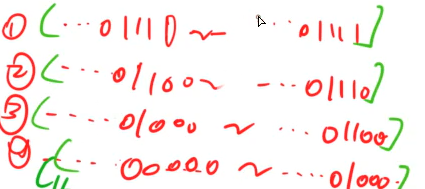
每一次去掉最后一个1

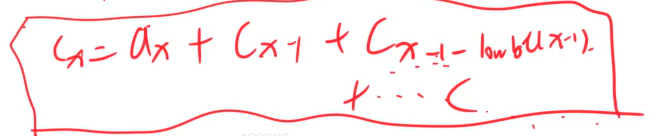
直到去k次，就把所有子节点找出来了。

• 如何通过子节点找到父节点（对应修改的操作）
  
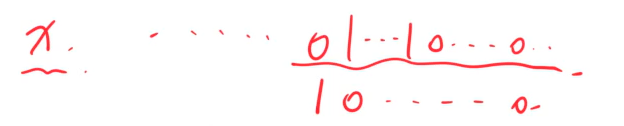
  修改完x之后，直接影响到的区间，是唯一的，一定是x最左边的1左边的0变成1的那个数P 区间内的数受影响，很明显 P= x + lowbit(x)，只要加上x最右边的1就可以变成以此增加就可以得到P
  
  
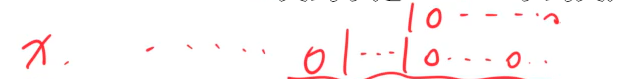
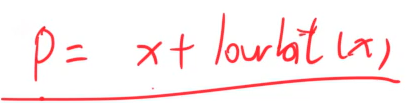
  所以这是一个迭代的过程，每往上走一次，末尾0的个数都会至少加一个，而最多只有log(x)位，这个过程最多只会进行log(x)次，该区间的每个数都被修改。
  tr[i]表示以i结尾的长度是lowbit(i)的区间和

• 修改某一个数： 修改以后其后面的数都要变化，从变化到尾；
  

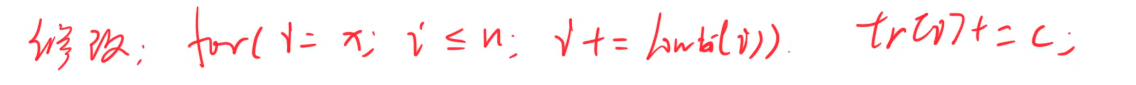
• 查询1 ~ x的和：从左到右加到x，注意tr数组下标要从1开始，不然当下标为0时，在这里进入死循环

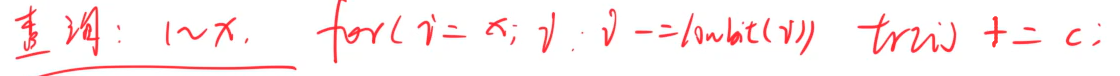
每一个循环都是log(n)的

简单应用：leetcode. 区域和检索 - 数组可修改
答案：307.区域和检索-数组可修改