【数据结构入门】——时间复杂度与空间复杂度

If you give someone a program, you will frustrate them for a day, If you teach them how to program, you will frustrate them for a lifetime.（如果你交给某人一个程序，你将折磨他一整天，如果你教某人如何编写程序，你将折磨他一辈子。）

前言：从今天开始正式进入数据结构的学习，在此之前先认识一下两个重要的名词：时间复杂度和空间复杂度。

1. 时间复杂度

1.1 时间复杂度的概念

在计算机科学中，算法的时间复杂度是一个函数（数学表达式），它定量描述了该算法的运行时间。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

1.2 大O的渐进表示法

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。
推导大 O 阶方法：
1、用常数 1 取代运行时间中的所有加法常数
2、在修改后的运行次数函数中，只保留最高阶项
3、如果最高阶项存在且不是 1 ，则去除这个项目相乘的常数。得到的结果就是大O阶。

有些算法的时间复杂度存在最好、平均和最坏的情况：

• 最坏情况：任意输入规模的最大运行次数（上界）
• 平均情况：任意输入规模的期望运行次数
• 最好情况：任意输入规模的最小运行次数（下界）

在实际中一般情况关注的是算法的最坏运行情况

1.2.1 常数阶

思考一下，下面这个算法的时间复杂度为什么不是O(3)，而是O(1)？

int sum = 0, n = 100;		//执行1次
sum = （1 + n） * n / 2;	//执行1次
printf（"%d", sum）;		//执行1次

那个算法的运行次数函数是f(n)=3，根据我们的推导大 O 阶方法，应该将常数项改为1，所以时间复杂度为O(1)。

  注：单纯的分支结构其时间复杂度也是O(1)。

1.2.2 线性阶

下面这段代码，它的循环的时间复杂度为O(n)

int i;
for（i = 0; i < n; i++）
{
	/* 时间复杂度为O(1)的程序步骤序列 */
}

1.2.3 对数阶

int count = 1;
while （count < n）
{
	count = count * 2;
	/* 时间复杂度为O(1)的程序步骤序列 */
}

由于每次count乘以2之后就距离n更近一分。即有多少个2相乘后大于n，则会退出循环。由2^x =n得到x=log₂n。所以这个循环的时间复杂度为O(logn)

1.2.4 平方阶

下面的例子是一个循环嵌套，它的内循环我们刚才已经分析过时间复杂度为O(n)

int i,j;
for（i = 0; i < n; i++）
{
	for（j = 0; j < n; j++）                       
	{                                      
		/* 时间复杂度为O(1)的程序步骤序列 */
	}                                      
}

外层循环也是同理，于是时间复杂度为O(n²)

那么下面这段代码呢？

int i,j;
for（i = 0; i < n; i++）
{
	for（j = i; j < n; j++）  /* 注意j = i而不是0 */
	{                                      
		/* 时间复杂度为O(1)的程序步骤序列 */
	}                                      
}

由于i=0时，内循环执行了n次，当i=1时，执行了n-1次，……当i=n-1时，执行了1次。所以总的执行次数为：
$n+(n-1)+(n-2)+...+1=$$\frac{n(n+1)}{2}$=$\frac{n^2}{2}$+$\frac{n}{2}$
用推导大O阶的方法，没有加法常数不考虑，只保留最高阶项，即$\frac{n^2}{2}$，去除与该项相乘的系数，即去除$\frac{1}{2}$，于是时间复杂度为 O(n²)

2. 常见的时间复杂度

执行次数函数	阶	非正式术语
12	O(1)	常数阶
2n+3	O(n)	线性阶
3n2+2n+1	O(n2)	平方阶
5log2n+20	O(logn)	对数阶
2n+3nlog2n+19	O(nlogn)	nlogn阶
6n3+2n2+3n+4	O(n3)	立方阶
2n	O(2n)	指数阶

注：经常把log₂n简写成logn

所消耗的时间从小到大依次是：
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)

3. 时间复杂度相关例子

3.1.1 实例1

// 计算Func1的时间复杂度？
void Func1(int N) {
	int count = 0;
	for (int k = 0; k < 100; ++k)
	{
		++count;
	}
	printf("%d\n", count);
}

对于 Func1 ，可以计算基本执行次数为 100 ，是一个常数，所以用大 O 的渐进表示法为 O(1)

3.1.2 实例2

// 计算strchr的时间复杂度？
const char* strchr(const char* str, int character);

strstr函数即在字符串中查找某个字符。时间复杂度为O(N)

3.1.3 实例3

// 计算BubbleSort的时间复杂度？
void BubbleSort(int* a, int n) {
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

可以看到，最好的情况就是执行 N 次(不是 1 次原因是即使不进行元素交换，此算法也会对数组遍历检查)。最差的情况就是计算 1、2、3……N-2、N-1 这个等差数列之和，即 $$\frac{(N-1)\ast N}{2}$$ ，那么要表示时间复杂度，就要用大 O 的渐进表示法，即去除影响不大的项，O(N²) 。

3.1.4 实例4

// 计算BinarySearch的时间复杂度？
int BinarySearch(int* a, int n, int x) {
	assert(a);
	int begin = 0;
	int end = n - 1;
	// [begin, end]：begin和end是左闭右闭区间，因此有=号
	while (begin <= end)
	{
		int mid = begin + ((end - begin) >> 1);
		if (a[mid] < x)
			begin = mid + 1;
		else if (a[mid] > x)
			end = mid - 1;
		else
			return mid;
	}
	return -1;
}

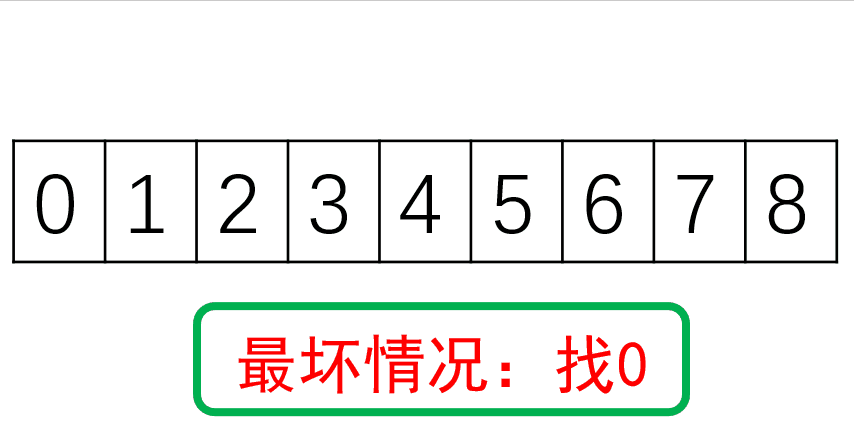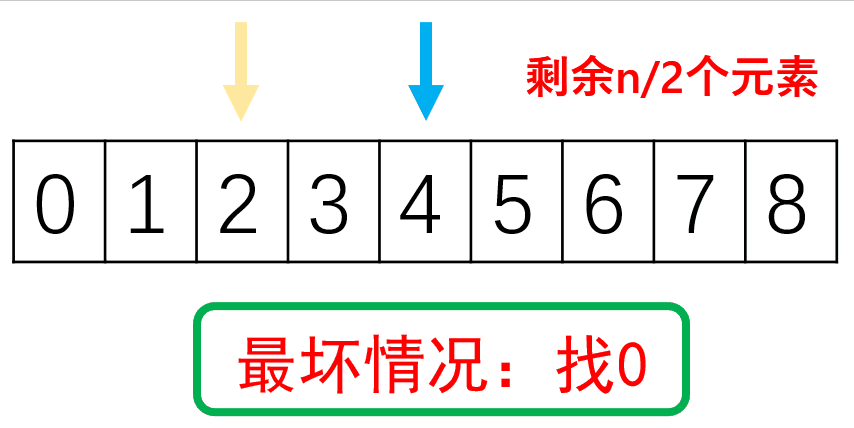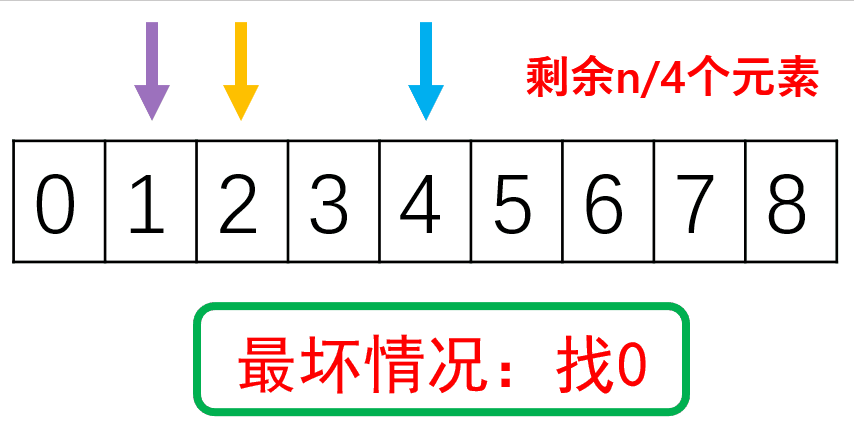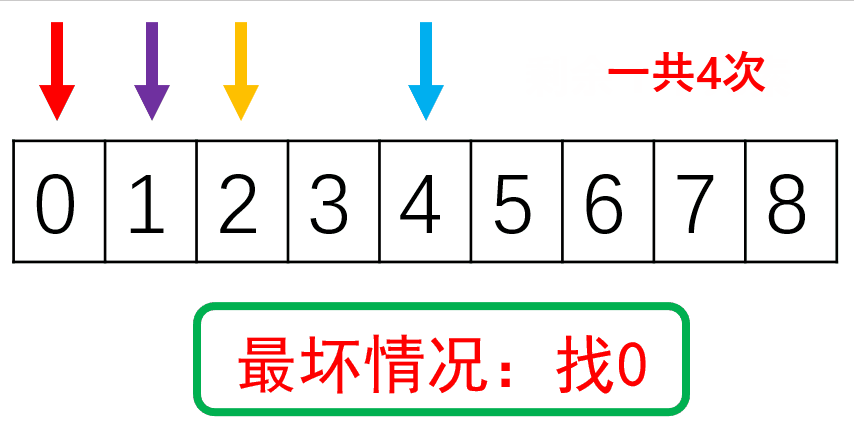
假设查找x次后还剩一个元素，则 $$1=\frac{N}{2^x}$$ 即x = log₂n，最坏情况为O(logn)，最好情况为O(1)。

3.1.5 实例5

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N) {
	if (0 == N)
		return 1;
 
	return Fac(N - 1) * N;
}

对于函数递归，我们只需要关心函数被调用几次即可。那么对于求阶乘的递归算法来说，函数被调用了 N 次，所以时间复杂度为 O(N) 。

3.1.6 实例6

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N) {
	if (N < 3)
		return 1;
 
	return Fib(N - 1) + Fib(N - 2);
}

4. 空间复杂度

• 空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时(额外)占用存储空间大小的量度。

• 空间复杂度不是程序占用了多少字节空间，而是变量(空间)的个数。即使想要计算程序占用了多大空间也没有意义。

• 空间复杂度计算规则与时间复杂度一样，都使用大 O 渐进表示法。

5. 空间复杂度的相关例子

5.1.1 实例1

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n) {
		assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

因为所占空间数为常数，所以空间复杂度为 O(1) 。

5.1.2 实例2

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n) {
	if (n == 0)
		return NULL;
 
	long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n; ++i)
	{
		fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
	}
	return fibArray;
}

占用的空间与参数 n 有关，栈区上的空间是可以重复利用的。所以空间复杂度为 O(N) 。

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N) {
	if (N == 0)
		return 1;
 
	return Fac(N - 1) * N;
}

Fac 函数被调用 N+1 次，每次调用都开辟一个栈帧，而这个栈帧又是常数。但是调用几次又参数 N 决定，所以空间复杂度为 O(N) 。

注：在刚才的计算中，可以发现我们并没有把形参的所占空间给算进去。这里需要注意的是，函数的形参是完成算法的条件，并不是额外开辟的一个临时空间。

6. 复杂度的相关练习

6.1.1 练习1

1、设某算法的递推公式是T(n)=T(n-1)+n，T(0)=1，则求该算法中第n项的时间复杂度为（）
A.O(n)
B.O(n^2)
C.O(nlogn)
D.O(logn)

解析：T(n) = T(n-1)+n =T(n-2)+(n-1)+n
=T(n-3)+(n-2)+(n-1)+n
…
=T(0)+1+2+…+(n-2)+(n-1)+n
=1+1+2+…+(n-2)+(n-1)+n

从递推公式中可以看到，第n项的值等于1到n的累加值，需要遍历n个元素
所以时间复杂度为n，选A。

6.1.2 练习2

2、消失的数字
题解：

int missingNumber(int* nums, int numsSize)
{
    int sum=0;
    for(int i=0;i<=numsSize;i++)
    {
        sum+=i;//求出 0~n 范围的和
    }
    int tmp=0;
    for(int i=0;i<numsSize;i++)
    {
        tmp+=nums[i];//求出数组和
    }
    return sum-tmp;
}

6.1.3 练习3

3、轮转数组

//三步翻转法
void reverse(int* nums, int left ,int right)
{
    while(left<right)
    {
        int tmp=nums[left];
        nums[left]=nums[right];
        nums[right]=tmp;

        left++;
        right--;
    }
}


void rotate(int* nums, int numsSize, int k)
{
    if(k>=numsSize)
    {
        k%=numsSize;
    }
    reverse(nums, 0, numsSize-k-1);
    reverse(nums, numsSize-k, numsSize-1);
    reverse(nums, 0, numsSize-1);
}

OK，以上就是本期知识点“复杂度”的知识啦~~ ，感谢友友们的阅读。后续还会继续更新，欢迎持续关注哟~
如果觉得收获满满，可以点点赞👍支持一下哟~