【现代密码学原理】——分组加密的工作模式（学习笔记）

📖 前言：本章继续讨论对称密码，首先讨论多重加密，然后介绍分组密码的工作模式。

---

🕒 0. 思维导图

🕒 1. 多重加密

🕘 1.1 双重DES

🕤 1.1.1 数据加密标准DES

🕤 1.1.2 为什么需要多重加密

表 穷尽密钥搜索所需的平均时间
$\begin{array}{ccccc}\text{ 密钥大小/位 }& \text{ 密 码 }& \text{ 密钥个数 }& \text{ 每微秒执行 }1\text{ 次解密的时间 }& \text{ 每微秒执行 }1000\text{ 万次解密的时间 }\\ 56& \text{ DES }& 2^{56}\approx 7.2\times 10^{16}& 2^{55}\mathrm{ns}=1.125\text{ 年 }& 1\text{ 小时 }\\ 128& \text{ AES }& 2^{128}\approx 3.4\times 10^{38}& 2^{127}\mathrm{ns}=5.3\times 10^{21}\text{ 年 }& 5.3\times 10^{17}\text{ 年 }\\ 168& 3\mathrm{DES}& 2^{168}\approx 3.7\times 10^{50}& 2^{167}\mathrm{ns}=5.8\times 10^{33}\text{ 年 }& 5.8\times 10^{29}\text{ 年 }\\ 192& \mathrm{AES}& 2^{192}\approx 6.3\times 10^{57}& 2^{191}\mathrm{ns}=9.8\times 10^{40}\text{ 年 }& 9.8\times 10^{36}\text{ 年 }\\ 256& \mathrm{AES}& 2^{256}\approx 1.2\times 10^{77}& 2^{255}\mathrm{ns}=1.8\times 10^{60}\text{ 年 }& 1.8\times 10^{56}\text{ 年 }\\ 26\text{ 个字符的排列组合 }& \text{ 单字母代替 }& 2!=4\times 10^{26}& 2\times 10^{26}\mathrm{ns}=6.3\times 10^9\text{ 年 }& 6.3\times 10^6\text{ 年 }\end{array}$

DES在穷举攻击下比较脆弱，有两种代替方案：

• 设计全新的算法，如AES
• 用DES进行多次加密，使用多个密钥

🕤 1.1.3 过程

多次加密的最简单形式是进行两次加密，使用两个密钥，如下图所示
给定明文P，密钥K1、K2

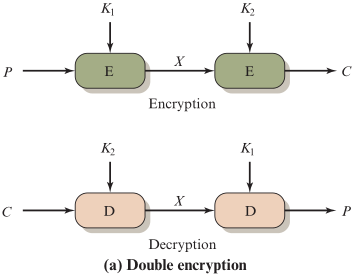
【第一次加密】
加密算法E 读取明文P 与 本次加密的密钥K1 ，生成密文X：
$\mathbf{X}=\mathbf{E}({\mathbf{K}}_1，\mathbf{P})$

【第二次加密】
加密算法E 读取密文X 与 本次加密的密钥K2 ，生成密文C：
$\mathbf{C}=\mathbf{E}({\mathbf{K}}_2，\mathbf{X})=\mathbf{E}({\mathbf{K}}_2，\mathbf{E}({\mathbf{K}}_1，\mathbf{P}))$

【第一次解密】
解密算法D 读取密文C 与 第二次加密的密钥K2 ，还原明文X：
$\mathbf{X}=\mathbf{D}({\mathbf{K}}_2，\mathbf{C})$

【第二次解密】
解密算法D 读取密文X 与 第一次加密的密钥K1 ，还原明文X：
$\mathbf{P}=\mathbf{D}({\mathbf{K}}_1，\mathbf{X})=\mathbf{D}({\mathbf{K}}_1，\mathbf{D}({\mathbf{K}}_2，\mathbf{C}))$

DES 不会出现下述情况：
$\mathbf{E}({\mathbf{K}}_2，\mathbf{E}({\mathbf{K}}_1，\mathbf{P}))=\mathbf{E}({\mathbf{K}}_3，\mathbf{P})$

也就是说双重DES 对应的映射 无法用某个单DES来表示，不会被约化为单次加密。

• 对于DES，这种双重加密的方法共涉及到两个密钥，密钥长度共56*2=112位
• 密钥空间变大，对密钥发起穷举攻击的难度增加

❗ 转载请注明出处
作者：HinsCoder
博客链接：🔎 作者博客主页

🕤 1.1.4 中间相遇攻击

• 可以对双重DES 发起 中间相遇攻击
• 它不依赖于DES的任何特殊性质，对所有的分组密码都有效

假设$\mathbf{C}=\mathbf{E}({\mathbf{K}}_2，\mathbf{E}({\mathbf{K}}_1，\mathbf{P}))$，则有
$\mathbf{X}=\mathbf{E}({\mathbf{K}}_1，\mathbf{P})=\mathbf{D}({\mathbf{K}}_2，\mathbf{C})$

$\mathbf{X}=\mathbf{E}({\mathbf{K}}_1，\mathbf{P})$

• 给定明密文对 $(\mathbf{P},\mathbf{C})$，将𝑷按所有可能的密钥${\mathbf{K}}_1$进行加密，得到了$2^{56}$个不同的𝑿，按值排序放在一个表内

$\mathbf{X}=\mathbf{D}({\mathbf{K}}_2，\mathbf{C})$

• 将C用所有可能的密钥${\mathbf{K}}_2$解密，每解密一次就将解密结果与𝑿表中的值比较，直到两值相等，保存当前的$({\mathbf{K}}_1,{\mathbf{K}}_2)$

• 使用另外的明密文对$(\mathbf{P},\mathbf{C})$来验证$({\mathbf{K}}_1,{\mathbf{K}}_2)$
  若加密𝑷恰好生成了𝑪，那么$({\mathbf{K}}_1,{\mathbf{K}}_2)$就是正确的密钥

多选题
关于中间相遇攻击，以下说法正确的有：
A. 中间相遇攻击可以针对任意分组密码
B. 原理为$\mathbf{X}=\mathbf{E}({\mathbf{K}}_1，\mathbf{P})=\mathbf{D}({\mathbf{K}}_2，\mathbf{C})$
C. 这种攻击依赖于已知的明密文对
D. 使用两组明密文对基本上就可以猜出双重DES的正确密钥
答案：全选

🕘 1.2 三重DES

• 应对中间相遇攻击，可以使用三个不同的密钥进行三次加密，发起穷举攻击也需要尝试𝟐^𝟏𝟔𝟖次
• 168位的密钥长度并不现实，但仍有许多Internet应用采纳了该加密方案，如电子邮件中的PGP和S/MIME协议

【第一次加密】
加密算法E 读取明文P 与 本次加密的密钥K1，生成密文A：
$\mathbf{A}=\mathbf{E}({\mathbf{K}}_1，\mathbf{P})$

【第二次加密】
解密算法D 读取明文X 与 本次加密的密钥K2，生成密文B：
$\mathbf{B}=\mathbf{D}({\mathbf{K}}_2，\mathbf{A})=\mathbf{D}({\mathbf{K}}_2，\mathbf{E}({\mathbf{K}}_1，\mathbf{P}))$

【第三次加密】
加密算法E 读取明文B 与 本次加密的密钥K1，生成最终的密文C：
$\mathbf{C}=\mathbf{E}({\mathbf{K}}_1，\mathbf{B})=\mathbf{E}({\mathbf{K}}_1，\mathbf{D}({\mathbf{K}}_2，\mathbf{E}({\mathbf{K}}_1，\mathbf{P})))$

【第一次解密】
解密算法D 读取密文C 与 第三次加密的密钥K1，还原明文B：
$\mathbf{B}=\mathbf{D}({\mathbf{K}}_1，\mathbf{C})$

【第二次解密】
加密算法E 读取密文B 与 第二次加密的密钥K2，还原明文A：
$\mathbf{A}=\mathbf{E}({\mathbf{K}}_2，\mathbf{B})=\mathbf{E}({\mathbf{K}}_2，\mathbf{D}({\mathbf{K}}_1，\mathbf{C}))$

【第三次解密】
解密算法D 读取密文A 与 第一次加密的密钥K1，还原明文P：
$\mathbf{P}=\mathbf{D}({\mathbf{K}}_1，\mathbf{A})=\mathbf{D}({\mathbf{K}}_1，\mathbf{E}({\mathbf{K}}_2，\mathbf{D}({\mathbf{K}}_1，\mathbf{C})))$

🕤 1.2.1 2-Key-3-DES

• 使用两个密钥的三重DES 已经广泛地替代了DES
• 当前还没有对3DES的可行攻击方法，发起穷举攻击也要$5\times 10^{33}$数量级
• 三次加密过程使用的不全是加密算法

单选题
关于DES说法不正确的是？
A. DES一次只能加密64位的明文分组
B. DES的基础结构是Feistal结构
C. DES易受穷举密钥攻击
D. 3DES是DES的一种安全方案，必须用到三把不同的密钥
答案：D（解析：可以有两把）

🕒 2. 分组加密工作模式

• Bob 要给Alice 发送消息，打算使用分组密码中的DES来为消息加密

• 现在消息长度刚好等于分组长度64bit，DES可以直接将其加密生成一个64bit的密文输出

• 若Bob 认为将消息加密一次还不够安全，也可以使用2DES 或2K-3DES 来为这64bit的消息进行多次加密，发送给Alice

• 分组密码DES 在进行加密操作时，输入的是固定长度64位的明文分组，输出的也是固定长度的密文分组

• 当Bob要发送的消息大于分组长度64bit，仍要使用DES来进行加密，那么该如何操作呢？

• 将要加密的Message 拆分为多个分组，每个分组长度为64bit，最后一组若不足64位则用0补齐

• 若Message的各个分组，在进行加密的时候都使用同一种密钥K来进行，则生成的密文分组会存在一些统计规律特征，引发许多安全问题

• 如何将分组密码(如DES、AES) 应用到各种实际情景(如加密、认证)呢？

• NIST 定义了五种工作模式，使得分组密码更适应实际需要

🕘 2.1 电码本ECB

• 电码本是最简单的分组密码工作模式，明文长度若大于分组长度，将其填充并划分为多个分组

• 一次加密一个明文分组${\mathbf{P}}_{\mathbf{i}}$，每次使用相同的密钥$\mathbf{K}$

• 对于给定的密钥$\mathbf{K}$ ，任何固定长度的明文分组${\mathbf{P}}_{\mathbf{i}}$都只有唯一的一个密文分组${\mathbf{C}}_{\mathbf{i}}$和它对应

• 加密就像查阅一本密码本，根据明文就可以找出相应的密文

• 若明文被填充划分成了N个明文分组，则ECB 的加密过程可以记作：
  ${\mathbf{C}}_{\mathbf{i}}=\mathbf{E}(\mathbf{K}，{\mathbf{P}}_{\mathbf{i}})$      $\mathbf{i}=1,2\dots \mathbf{N}$

• 一次解密一个密文分组${\mathbf{C}}_{\mathbf{i}}$，每次使用相同的密钥$\mathbf{K}$

• ECB 的解密过程记作：
  ${\mathbf{P}}_{\mathbf{i}}=\mathbf{D}(\mathbf{K}，{\mathbf{C}}_{\mathbf{i}})$      $\mathbf{i}=1,2\dots \mathbf{N}$

• 若一段明文消息中有两个分组${\mathbf{P}}_1$和${\mathbf{P}}_2$是相同的，那么在使用相同的密钥K加密后，密文消息中也会出现2个相同的分组${\mathbf{C}}_1$和${\mathbf{C}}_2$

• 密码分析者可利用这些规律特征来破译

• 电码本ECB 适用于数据较少的情况

• Bob和Alice 进行通信，约定使用AES 来进行消息的加密，Bob需要将密钥K安全地传递给Alice。

• 可以使用ECB模式，运用DES加密算法 为128bit的密钥K 进行加密

🕘 2.2 密文分组链接CBC

• CBC可以将相同的明文分组加密成不同的密文分组

• 明文消息被填充划分为多个明文分组${\mathbf{P}}_1,{\mathbf{P}}_2\dots {\mathbf{P}}_{\mathbf{N}}$

• 先将第一个明文分组${\mathbf{P}}_1$与 等长度的初始向量$\mathbf{IV}$进行XOR运算，生成等长度的一个输出

• 加密算法E 读取 XOR运算结果 与 密钥K ，生成第一个密文分组${\mathbf{C}}_1$

• 将第二个明文分组${\mathbf{P}}_2$与上一步生成的密文分组${\mathbf{C}}_1$进行异或运算，生成一个等长度的输出

• 加密算法E 读取 XOR运算结果 与 密钥K ，生成第二个密文分组${\mathbf{C}}_2$

• 重复操作直至所有明文分组均处理完毕

• CBC 的加密过程可以写作
  ${\mathbf{C}}_1=\mathbf{E}(\mathbf{K}，{\mathbf{P}}_1\oplus \mathbf{IV})$
  ${\mathbf{C}}_{\mathbf{i}}=\mathbf{E}(\mathbf{K}，{\mathbf{P}}_{\mathbf{i}}\oplus {\mathbf{C}}_{(}\mathbf{i}-1))$      $\mathbf{i}=2,3\dots \mathbf{N}$

• 就算存在相同的明文分组${\mathbf{P}}_1$和${\mathbf{P}}_2$

• “密文分组” ${\mathbf{C}}_1$是将${\mathbf{P}}_1$与$\mathbf{IV}$异或后 使用𝑲加密得来
  “密文分组” ${\mathbf{C}}_2$是将${\mathbf{P}}_2$=${\mathbf{P}}_1$ 与${\mathbf{C}}_1$异或后 加密得来

• CBC 的解密过程可以写作
  ${\mathbf{P}}_1=\mathbf{D}(\mathbf{K},{\mathbf{C}}_1)\oplus \mathbf{IV}$
  ${\mathbf{P}}_{\mathbf{i}}=\mathbf{D}(\mathbf{K},{\mathbf{C}}_{\mathbf{i}})\oplus {\mathbf{C}}_{(}\mathbf{i}-1)$      $\mathbf{i}=2,3\dots \mathbf{N}$

• CBC 适用于加密那些长度大于分组长度b的消息

• 由于CBC 的链接机制 以及 保密的初始向量$IV$，也使得它不仅用于加密，还可用于认证

多选题
A给B 发送一段长度为1M的消息，使用AES作为加密算法，约定密钥为K，采用CBC模式：
A. 使用的密码体制为对称密码，因为加密与解密用的是相同密钥K
B. 使用的密码类型为分组密码，因为AES一次可以同时加密128bit的明文
C. 消息被分为多个分组，依次使用AES进行加密处理，处理的方式为CBC工作模式
D. 使用CBC工作模式需要对最后分组的消息进行填充
答案：全选

🕘 2.3 密文反馈CFB

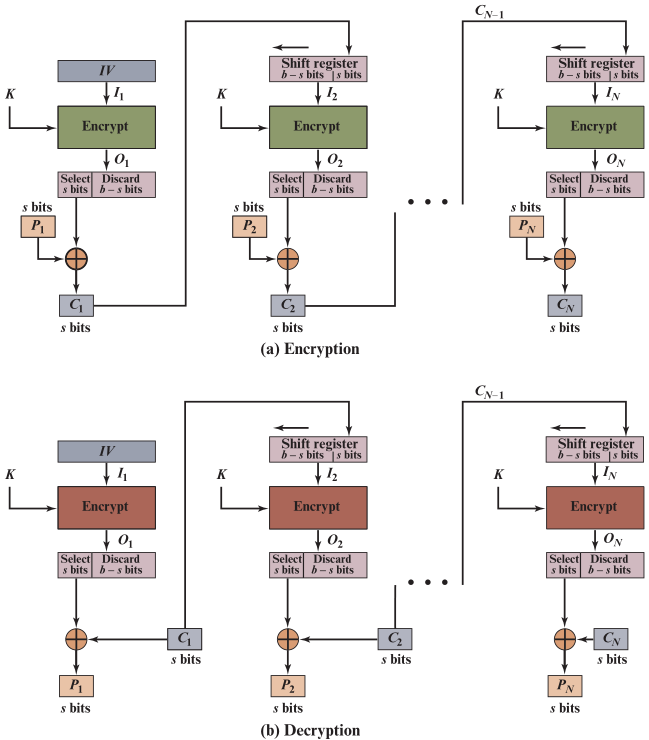
• 设定一个移位寄存器，大小为分组长度b位

• 移位寄存器的初始值为通信双方约定好的初始向量$\mathbf{IV}$，长度为$b$位

• 加密算法读取移位寄存器中的$\mathbf{IV}$ ，使用密钥$K$为其加密，生成一个$b$位的输出

• 密文反馈模式CFB 对明文的处理类似于流密码

• 发送方一次连续发送s位的消息分段给对方，CFB 每次就处理这s位的分段，将其加密成密文分段传递出去

• 加密算法生成了$b$位的输出

• 选取最左边的s位，与第一个明文分段${\mathbf{P}}_1$进行按位异或

• 产生了s位的密文分段${\mathbf{C}}_1$

• 移位寄存器中存放着$\mathbf{IV}$，将其左移s位，最右边空出来$s$位

• 将上一次生成的密文分段${\mathbf{C}}_1$填入到移位寄存器的最右边$s$位里

• 加密算法E 读取目前移位寄存器中的$b$位数据，并使用密钥K 对其加密，产生一个$b$位的输出

• 仍然从b位输出中选择最左边的s位 与明文分段${\mathbf{P}}_2$进行按位异或，生成密文分段${\mathbf{C}}_2$

• 继续重复操作，直到明文全部处理完毕

🕘 2.4 输出反馈OFB

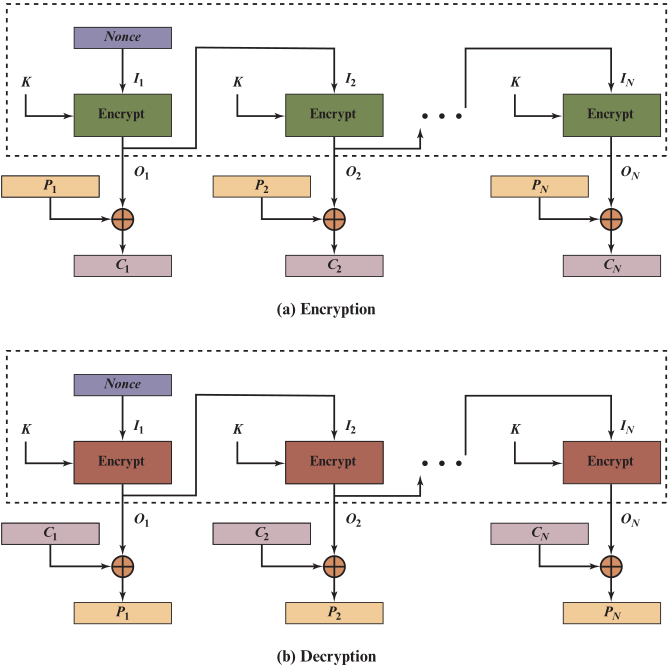
• 选取一个$b$位的初始化向量$\mathbf{IV}$ ，它随时间变化而变化，保证每次加密运算值都是唯一的

• 加密算法$E$读取这个初始向量，使用密钥$K$对其进行加密，生成b位的输出${\mathbf{O}}_1$

• 第一个明文分组${\mathbf{P}}_1$ 与加密算法的输出${\mathbf{O}}_1$进行按位异或，生成第一个密文分组${\mathbf{C}}_1$

• 加密算法E 将上一次的加密输出${\mathbf{O}}_1$再次使用密钥K进行加密，生成输出${\mathbf{O}}_2$

• 明文分组${\mathbf{P}}_2$与这个经过两次加密的输出${\mathbf{O}}_2$ 进行按位异或，生成第二个密文分组${\mathbf{C}}_2$

• 继续按照这种方法进行处理，明文分组${\mathbf{P}}_{\mathbf{i}}$都是与一个加密了$i$次的输出${\mathbf{O}}_{\mathbf{i}}$进行按位异或，得到密文

• 输出反馈模式OFB 也不需要填充明文消息，那么当最后一个明文分组${\mathbf{P}}_{\mathbf{N}}$的长度为$u<b$，加密了$N$次的输出${\mathbf{O}}_{\mathbf{N}}$只用它前面的u位参与异或运算

• 对任意一个明文分组进行处理生成密文时，都是与一个${\mathbf{O}}_{\mathbf{i}}$进行按位异或，而这个${\mathbf{O}}_{\mathbf{i}}$是初始向量通过若干次加密得来，与明密文无关，$取决于K、IV$

• 解密过程与CFB类似，也是将密文分组与一个特定的${\mathbf{O}}_{\mathbf{i}}$再次进行异或，还原出明文分组

无论是密文反馈模式CFB，还是输出反馈模式OFB，它们每一个分组的加密都要等待上一个加密流程的输出，所以无法并行地处理一段明文消息

🕘 2.5 计数器模式CTR

当确定了明文消息划分出的分组个数N后，就确定了N个计数器的值，加密后就确定了N个参与异或运算的输出值，可以并行地为明文分组进行异或

🕘 2.6 小结

模式	描述	典型应用
Electronic Codebook (ECB)	用相同的密钥分别对明文分组单独加密	单个数据的安全传输（如一个加密密钥）
Cipher Block Chaining (CBC)	加密算法的输入是上一个密文分组和下一个明文分组的异或	面向分组的通用传输；认证
Cipher Feedback (CFB)	一次处理输入的s位，上一个密文分组作为加密算法的输入，产生的伪随机数输出与明文异或后作为下一个单元的密文	面向数据流的通用传输；认证
Output Feedback (OFB)	与CFB类似，只是加密算法的输入是上一次加密的输出，并且使用整个分组	噪声信道上的数据流的传输（如卫星通信）
Counter(CTR)	每个明文分组都与一个经过加密的计数器异或。对每个后续的分组，计数器增1	面向分组的通用传输；用于高速需求

单选题
分组密码的工作模式中，符合以下特性的工作模式是哪个？
1）如果消息中有几个相同明文组，那么密文也会出现相同的密文分组
2）适合数据较少的情况，如加密密钥
A.ECB
B.CBC
C.CFB
D.OFB
答案：A

🕒 3. 中英文对照表

---

OK，以上就是本期知识点“分组加密的工作模式”的知识啦~~ ，感谢友友们的阅读。后续还会继续更新，欢迎持续关注哟📌~
💫如果有错误❌，欢迎批评指正呀👀~让我们一起相互进步🚀
🎉如果觉得收获满满，可以点点赞👍支持一下哟~

❗ 转载请注明出处
作者：HinsCoder
博客链接：🔎 作者博客主页