【数据库理论】关系模型 - 概念与理解

本文链接：https://blog.csdn.net/Hominid_Pro/article/details/144123113

数据模型

关系模式一种典型的数据库模型，它的成功也许会有偶然的成分，但一定离不开其背后的理论基础。在进一步讨论关系模型之前，不得不先了解另一个非常基础的概念： 数据模型（Data Model）。数据模型是对现实世界数据特征的抽象，它包括概念模型、逻辑模型、物理模型 3 个部分。

当我们试图在计算机中表示一个人物时，我们首先会考虑这个人物的哪些特征是我们目前所需要的。比如对教务系统中的一个学生对象而言，他/她的学号、姓名、电话、性别、籍贯等信息就是必须的，而他/她的身高、体重、兴趣爱好等信息可能就不是我们所关心的。此外我们还会关心有哪些实体会出现在我们的软件系统当中，以及这些实体之间会不会相互关联。比如教务系统中不仅有学生，还需要有教师、课程等实体。教师可以教授课程，学生可以选择课程。这都是站在用户的角度来对现实世界进行抽象，这就是概念模型，即按用户的观点对数据进行建模。

一旦我们规划好了整个软件系统中应该有哪些实体、实体具有什么属性，实体之间如何相互联系，接下来的任务就是如何在计算机中表示它们，我们不会直接操作内存或磁盘等存储介质来存储这些实体，而是使用逻辑的结构去表示它们，比如使用一个结构体表示一个实体，使用一个数组来表示同一类的实体，这就是逻辑模型，即按计算机的观点对数据进行建模。

最后，我们还要解决数据如何存储在物理介质上，比如是将一个实体的全部数据连续存储在一起（行式存储），还是将同一类实体的某个属性连续存储在一起（列式存储）。存储的方式非常重要，它决定了在查询这些数据时的性能。这就是物理模型，即描述了数据在储存介质上的组织结构。

现在再从完整的抽象过程来看数据模型，它的 3 层模型也就是抽象的 3 个步骤，每个层次都在关注数据，但数据的形式表现不同。概念模型的建立发生在数据库的设计阶段，数据库设计人员负责将现实世界中的客观对象抽象到信息世界中（即负责将客观对象转换为概念模型），而 DBMS 则负责将信息世界中的数据转换到机器世界中（即负责表示逻辑模型，并转换为物理模型）。
而我们即将要讨论的关系模型就是一种数据模型，它本质上也是一种抽象方法。它将所有的实体都统一的表示为一张二维表（这里是不严谨的描述，实际上关系不是二维的，甚至它都不是表），而表在数学中的定义就是 关系（Relation），所以这也是 关系模型（RM，Relational Model）名称的由来（并不是因为 RM 可以表示了实体之间的关系）。

关系模型的定义

关系模型最初是由 E.F.Codd 于 1970 年提出的，是建立在 逻辑学 和 集合论 之上的一种数学理论，所以关系模型是非常科学且稳定的理论模型。E.F.Codd 在定义关系模型的过程中，也曾多次修改其定义内容：

1970 年发表了《A Relational Model of Data for Large Shared Data Banks》，提出了关系模型的概念；
1981 年获得图灵奖时，阐述了论文《Relational Database: A Practical Foundation for Productivity》；
1985 年发表了《Is Your DBMS Really Relational?》和《Does Your DBMS Run By the Rules》，定义了数据库范式和十二条准则；
1990 年发表了专著《The Relational Model For Database Management Version 2》；

为避免歧义， E.F.Codd 特别使用术语 Relation、Tuple 和 Attribute 替代 Table、Row 和 Column （SQL 标准则是使用了后者作为术语） 。虽然关系模型是 E.F.Codd 提出的，但他表示任何人都可以对其进行改进。而关系模型定义的每次调整，并不是将先前的理论彻底推翻，而是进一步的补充和完善。比如 C.J Date 和 Hugh Darwen 合著的 《Databases, Types, and the Relational Model: The Third Manifesto》 就是对 E.F.Codd 关系模型定义的补充（书中定义的关系模型和 E.F.Codd 最初的愿景是一致的，其中的定义不仅详细而且严格，甚至可以说是权威的）。后续的内容都是基于这一本书展开的，如果你对 RM 的各种细节感兴趣，可以去仔细阅读这本书（书中的很多示例都是以 Tutorial D 语言展示的，该语言也是由 C.J Date 和 Hugh Darwen 提出的，专门用于关系数据库理论的教学。为此两人甚至还开发了 Rel 数据库，是一个开源、跨平台并且严格遵循关系理论的 RDBMS）。

模型中的概念

关系

关系由 2 部分组成，即 标题（Heading）和主体（Body）。其中标题是 属性（Attribute） 的集合，属性包括名称和类型（在描述属性时经常会省略描述其类型）：

属性的类型可以相同，并且可以是任意类型，早期的关系文献习惯性将“类型”称为域（Domain）。
属性的名称不可以相同。

标题中属性的个数称为该关系的 度/目（Degree） 或 元（arity） ，关系的度可以为 0：

即不包含任何属性的关系，这种零元关系依然可以包含元组，而此时元组的度也必须为 0，这种元组被称为 零元（Nullary） 或 空元组（Empty Tuple） 。根据元组相等的条件可以得出，所有的 0 元组都是相同的，所以关系模型中只有一个零元。如果该关系包含元组 （即包含一个零元） ，则它被称为 TABLE_DEE ，简称 DEE ，否则它被称为 TABLE_DUM ，简称 DUM 。和零元一样，关系模型中有且只有一个 DEE 和 DUM（如果你对 DEE 和 DUM 名称来由感兴趣，可以参考 C.J.Date 的《SQL and Relational Theory》，中文译本为《SQL与关系数据库理论》）。
零元没有实际用途，但在关系理论中有存在的必要性：类似空集是任意集合的子集。标题的子集依然是标题，元组的子集依然是元组，所以零元标题是任意关系标题的子集，零元是任意元组的子集。
DEE/DUM 在关系理论中同样有存在的必要性：
- 类似 “零” 在算术中扮演的角色，它们是用于表示 true 和 false 的关系：比如 “查询年龄大于 45 的员工，在空属性上的投影”：DEE 表示 true （因为元组就是一个真命题），DUM 表示 false （主体为空，表示命题为假）。如果存在这样的员工，则查询结果为 DEE，表示存在，否则查询结果为 DUM，表示不存在（由于 SQL 没有提供表示真/假的表，所以只能通过 count() 获取其数量，再提取单行结果中的列值，判断该值是否为 0）。
- 0 是算术加法 + 的单位元，1 是算术乘法 * 的单位元，即 x+0 、 0+x 、 1*x 、 x*1 都等价于 x ，所以类似的：DEE 是关系连接 ⋈ 的单位元， R ⋈ DEE 和 DEE ⋈ R 都等价于 R 。而 R ⋈ DUM 和 DUM ⋈ R 的结果则类型和 R 相同的空关系（如果理解这部分内容存在困难，则需要先了解连接运算的规则，我会在另一篇文章中进行分享：【数据库理论】关系模型 - 代数运算符（二））。

主体是 元组（Tuple） 的集合，元组包括属性和值：

元组的属性就是标题的属性，所以元组的类型就是标题中属性的类型（注意：元组 t 和包含元组 t 的关系 r 具有两种不同的类型，尽管这两种类型具有相同的标题）。
分量（Component） 就是元组中的某个属性对应的值，全部分量的集合就是该元组的值。

主体中元组的个数称为该关系的 基数（Cardinality） ，关系的基数可以为 0：

即主体中没有元组，则该关系是一个 空关系（Empty Relation） 。
空关系不止一个，不同类型的空关系并不相等（注意空关系和零元关系是两个不同的概念，请勿混淆）。

主体中的两个元组相等当且仅当它们包含相同的属性且全部分量均相等。

视图

上述内容描述的关系指的是直接定义在数据库中的关系（RDBMS 必须提供定义并解释关系类型的模块），所以也被称为 真实关系变量（Real Relvar） ，而 虚拟关系变量（Virtual Relvar） 则是通过关系代数运算推导出来的，它是一个命名的关系表达式，有时也被称为 视图（View） 。出于关系代数的闭包性，所以虚拟关系变量也是关系变量。它的值就是对该关系表达式进行求值的结果（如果理解这部分内容有困难，则需要了解关系变量和关系代数的相关内容。关系变量的内容稍后我们会有介绍。而关系代数的内容我会在另一篇文章中进行分享：【数据库理论】关系模型 - 代数运算符（一））。

虽然虚拟关系变量是从真实关系变量推导出来的，但在关系理论中两者没有本质区别：一种最常见的错误认知就是：真实关系变量对应着实际存储，而虚拟关系变量没有（从目前 RDBMS 的实现角度来看，这个理解没有问题。但站在关系理论的角度来看，关系模型和其实现是独立的，关系模型刻意地不去定义和物理存储相关的内容，凡是涉及存储细节的描述，都不属于关系模型的内容，而属于实现的范畴。正如单纯地讨论连接操作效率低是无意义的，只能说实现在处理连接操作时的方式有快有慢，实现完全可以将两个关系的连接结果以物理方式存储下来，再进行查询）。

RDBMS 在实现过程中，普遍的方式是关系对应着实际存储，而视图没有。所以在此前提下，有人提出了 快照（Snapshot） 的概念，它和视图一样，也是导出关系，但对应着实际存储，这些数据是根据基本关系推导出来的，但却是独立的副本，所以有时也被称为 物化视图（Materialized View） （由于涉及物理存储的内容，所以物化视图不属于关系理论的讨论范畴）。

视图的更新：目前为止，视图更新还处于研究阶段，不同的专业人士对此抱有不同的想法。但可以肯定的是视图确实可以被更新，但只能更新那些理论上可以进行更新的视图。

键

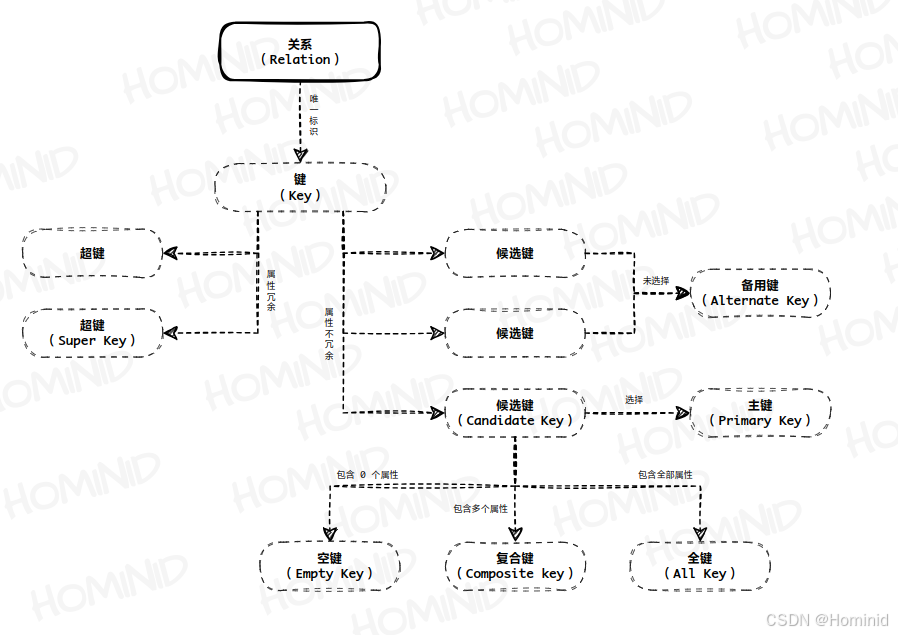
键（Key） 是关系中的一个属性组，这些属性能唯一标识一个元组。键作用于关系变量而不是元组，其本质是一种完整性约束：主键对应“实体完整性”约束，外键对应“引用完整性”约束。

超键（SK，Super Key） ：如果从键的属性组中移除某个属性，剩余的属性仍然能唯一标识一个元组，则将这个键称为“超键” （即有冗余属性）。

候选键（CK，Candidate Key） ：如果从键的属性组中移除某个属性，剩余的属性无法再唯一标识一个元组，则将这个键称为“候选键”（即无冗余属性）。考虑到属性组中的属性个数：

最简单的情况下，属性组中只包含一个属性。
如果属性组中不包含任何属性，即它是一个空集，则将该候选键称为 空键（Empty Key） ，这种关系最多只能包含一个元组。
如果属性组中的属性不止一个，则将该候选键称为 复合键（Composite key） 。
如果属性组中包含了关系的全部属性，则将该候选键称为 全键（All Key） 。

关系的候选键可能不只一个。可以指定其中一个作为唯一标识，并将其称为 主键（PK，Primary Key） ，而将其他未选择的候选键称为 备用键（Alternate Key） 。关系模型要求每个关系至少有一个“候选键”，但没有要求必须有“主键” （历史上关系模型曾经要求关系必要具有主键，但这并不重要，因为候选键和主键并没有本质区别，认为某个候选键比其他候选键更重要只是心理作用，所以说每个关系至少有一个“主键”也没有什么逻辑问题）。

根据上述分析，可以看出主键一定是候选键，而候选键一定不是超键（注意：有的书籍在描述超键定义时，没有强制要求超键必须有冗余属性，在这种情况下，则可以认为候选键一定是超键，不过这一细节区别并不会影响对关系理论的理解）。

外键（FK，Foreign Key） 用于将多个关系“关联”起来，它表示了两个关系之间的内在联系：假设 K 和 FK 分别是关系 R1 和 R2 标题的子集，它们包含相同的属性（如果对应属性的名称不同，则可以借助“重命名”运算符），并且 K 是 R1 的候选键。此时如果关系 R2 中的每个元组的 FK 值都等于关系 R1 中某个元组的 K 值（必然唯一），则称 FK 是关系 R2 的“外键”。有时会将包含外键的关系 R2 称为 从表（Slave Table） 或 子表（Child Table） ，将关系 R1 称为 主表（Master Table） 或 父表（Parent Table） 。（如果你第一次知晓外键的概念，可能会觉得定义有些复杂，或许你可以这么理解：K 是 R1 的候选键，所以每个不同的 K 都对应着关系 R1 中的一个唯一实体，而 R2 中每条元组的 FK 对应的值实际上就是引用 R1 中的实体）。

外键引用的不一定为关系的主键，也可以是任意一个候选键，所以可以认为外键引用的可以是具有唯一约束的属性组。关系模型不允许值为 null，但对于支持 null 的 DBMS 而言：由于唯一约束允许对应属性的值为 null，所以外键的值也可以为 null。

关系可以有多个外键。此外外键可以引用关系自身，这种外键被称为 自引用（Self-Referencing） 或 递归外键（Recursive FK） ，它表示了关系内部的联系，比如：

┌─────┬──────┬─────┬─────┬─────────┐
│  ID │ Name │ Age │ ... │ Monitor │
├─────┼──────┼─────┼─────┼─────────┤
│ 801 │ Kate │  19 │ ... │     803 │
│ 802 │ Jack │  20 │ ... │     803 │
│ 803 │ Lisa │  19 │ ... │     803 │
│ 804 │ Bob  │  17 │ ... │     803 │
└─────┴──────┴─────┴─────┴─────────┘
其中，ID 是学生表的主键，Monitor 是学生表的外键并且它引用了本表的 ID，因为 Monitor 必须是某个存在的学生。

关系变量和关系值

关系的标题是固定的，而关系中的元组是变化的，所以关系本质上是一种变量（诸多文献在描述这些概念时，都统一使用了“关系”一词，具体含义可从上下文中加以区分）：

“关系”也被称为 关系变量（Relvar，Relation Variable） ；
“关系的标题”也被称为 关系模式（Relation Schema） ，它代表关系变量的类型，两个关系模式相等意味着对应属性的名称和类型均相同；
“关系的主体”也被称为 关系值（Relation Value） ，即 关系实例（Relation Instance） ；

类似的，数据库存储的数据也是变化的，所以数据库本质上也是一种变量：

“数据库”也被称为 数据库变量（Dbvar，Database Variable） ，它是一个 元组类型的变量 ，该数据库中的每个关系变量都是该元组的一个分量（即该元组的每个属性都是 RVA），除此之外该元组没有其他分量。更新数据库中的某个关系变量就是在更新该数据库变量；
该元组的类型也被称为 数据库模式（Database Schema） ，它代表数据库变量的类型；
该元组的值也被称为 数据库值（Database Value） ，即 数据库实例（Database Instance） ，也被称为 数据库状态（Database State） 或 数据库快照（Database Snapshot） ；

模型的组成

按照《Databases, Types, and the Relational Model: The Third Manifesto》的描述，关系模型由以下 5 部分组成：

开放的类型集合：关系的属性是具有类型的，而属性可以是任意类型的，关系模型会假设有一系列可以使用的类型，比如整数、字符、字符串、日期、时间等简单类型，以及数组、集合、列表、XML、JSON、TVA、RVA 等复杂类型（注：TVA 指的是 Tuple Valued Attribute，RVA 指的是 Relation Valued Attribute）。考虑到对 AND 、OR 、NOT 等逻辑运算的支持，所以除 bool 类型外，关系模型未强制规定 RDBMS 必须定义哪些类型以及这些类型应该具有什么样的特性。因为类型及其语义属于“类型理论”的讨论范畴，这么做的好处是将“关系模型”与“类型理论”完全独立开，互不影响。而随着新类型的引入，RDBMS 就可以支持更丰富的特性，比如 XML 特性、JSON 特性、面向对象特性。
定义并解释关系类型的模块：关系本身也是一种类型，关系模式指的就是关系的类型，定义关系类型就是定义一个谓词，该类型的关系变量就是该谓词的真命题；
定义关系变量的模块：关系模型只有一种数据结构，所以只允许关系类型的变量（但这种限制只作用于关系系统内部，RDBMS 在实现过程中还是可以定义整数类型、数组类型、元组类型等各种类型的变量）；
关系赋值运算符：在我的另一篇文章中有详细描述：【数据库理论】关系模型 - 关系运算符；
关系代数运算符：在我的另一篇文章中有详细描述：【数据库理论】关系模型 - 代数运算符（一）、【数据库理论】关系模型 - 代数运算符（二）；

对关系模型的理解

对关系理论的理解

关系的标题本质上是谓词，是对元组进行判断的真值函数 （即要求函数返回真） 。而关系的元组本质上是一个真命题，即使用相应类型的参数替代谓词的占位符，比如：

┌─────┬──────┬─────┬──────┬────────┐
│  ID │ Name │ Age │ Dept │ Salary │
├─────┼──────┼─────┼──────┼────────┤
│ 801 │ Kate │  29 │ D1   │ 20K    │
│ 802 │ Jack │  30 │ D2   │ 30K    │
└─────┴──────┴─────┴──────┴────────┘

员工 ID 的姓名为 Name，年龄 Age 岁，在 Dept 部门工作，所得工资为 Salary：

员工 801 的姓名为 Tom，年龄 29 岁，在 D1 部门工作，所得工资为 20K。
员工 802 的姓名为 Jack，年龄 30 岁，在 D2 部门工作，所得工资为 30K。

按照“封闭世界假设”，未出现在关系中的元组则是伪命题。所以在关系数据库不仅仅是数据的集合，更是事实的集合。但由于 谓词逻辑 理论本身的局限性，关系数据库无法验证某个元组是否确实真实，它只能假设这些数据是真实的。虽然无法保证真实性，但通过完整性约束，关系数据库可以保证数据的一致性。

数据一致不代表数据真实，但数据不一致则意味着一定包含了伪命题（严格来说，事务 ACID 属性中描述的一致性实际上说的就是正确性）。

对关系模型的支持

关系理论的正确性：
关系模型不是定义和概念的临时拼凑，而是建立在严格的数学理论基础之上，其稳定性和正确性不容质疑。
关系理论和其实践之间存在差异，现在商用的 RDBMS 都没有完全遵守 E.F.Codd 的所有准则（或者 C.J Date、Hugh Darwen 等人所描述的关系理论），严格来说这些 RDBMS 不是关系型的（有时被称为“伪关系数据库管理系统”）。
作为这些关系型数据库标准语言的 SQL 也不是关系化的语言，它在很多方面也违背了关系理论，导致 SQL 语言本身存在问题，而 SQL 标准也在一直在修复这些问题。