0.网络流的相关概念
-
网络流(network-flows):求源点到汇点间的最大水流量
在有向图G=(V,E)中:- 容量限制:f[u,v] (边初始流量) <= c[u,v] (边最大容量)
- 反对称性:f[u,v] = - f[v,u]
- 流量平衡:结点的流量和等于流出该结点的流量和
满足上述三个性质就是一个合法的网络流了。
-
可行流:- 每条弧(u,v)上给定一个实数f(u,v),满足:有
0<= f(u,v) <= c(u,v)(容量),则称为弧(u,v)上的流量。 - 源点流出量等于整个网络的流量;汇点流入量等于整个网络的流量;中间点总流入量等于总流出量
- 每条弧(u,v)上给定一个实数f(u,v),满足:有
最大流相关算法有两种解决思想, 一种是增广路算法思想, 另一种是预流推进算法思想。
增广路算法(Ford-Fulkerson思想):关键在于如何找出增广路径,如何更新流量。
预流推进算法思想:
1. 基于增广路算法思想的最大流算法
增广路径就是:找出一条流量不满,未达到容量上限。然后通过bfs或dfs算法来找出增广路径来更新流量。
直接来样例:(参考网上的博客以及百度文库,文章后面已经标明)
在刚开始存边的时候,我们会初始化正向边为其初始流量,反向边初始为0(反向边是原图没有的,模拟的)。在增广路径更新流量的过程中,正向边流量减去路径最小流量,反向边流量添加路径最小流量。为什么要添加反向边,为了后面我们不流正向边或把正向边的一些流量分配给其他边。

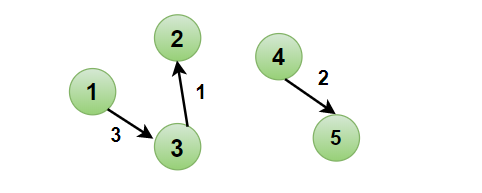
☞ 第一条增广路径: 1→2→3→5,路径最小流量为2,整个网络的最大流量Maxflow =2,然后更新路径上每条边的流量。然后2→3边容量为0了。

☞ 第二条增广路径: 1→2→4→5,路径最小流量为2,整个网络的最大流量Maxflow =2+2,然后更新路径上每条边的流量。然后1→2边的容量为0了。

☞ 第三条增广路径: 1→3→4→5,路径最小流量为1,正向边回退并分配1流量给2→4边,我们默认由1→5边减少了1流量,整个网络的最大流量Maxflow =2+2+1,然后更新路径上每条边的流量。

☞ 第四条增广路径: 1→3→5,路径最小流量为2,整个网络的最大流量Maxflow =2+2+1+2,然后更新路径上每条边的流量。再然后3→5边的容量为0了。

到这里我们基于搜索的所有增广路径全部找完,也就是找不到一条路径容量不为0的增广路径。
1.1 Edmonds-Karp算法(EK算法,SAP)
Edmonds-Karp算法:从源点开始做bfs,不断地修改delta量,直到到汇点与源点不连通,也就是找不到增广路径为止。
每进行一次增广需要的时间复杂度为 bfs 的复杂度 + 更新残余网络的复杂度, 大约为 O(m)(m为图中的边的数目), 需要进行多少次增广呢, 假设每次增广只增加1, 则需要增广 nW 次(n为图中顶点的数目, W为图中边上的最大容量), .
EK算法时间复杂度:O(n * m * m)
- 基于邻接矩阵实现的EK算法:
#include<stdio.h>
#include<queue>
#include<string.h>
#include<algorithm>
using namespace std;
const int maxn = 300;///邻接矩阵适合点比较小的图
const int MAX = ((1<<31)-1);
int n;
int pre[maxn];///存储当前边的起点
bool vis[maxn];//标记访问点
int mp[maxn][maxn];///记录每条边的流量
bool bfs(int s,int t){
queue<int>que;
memset(vis,0,sizeof(vis));
memset(pre,-1,sizeof(pre));
pre[s] = s;
vis[s] = true;
que.push(s);
while(!que.empty()){
int u = que.front();
que.pop();
for(int i=1; i<=n; i++){
if(mp[u][i]&&!vis[i]){
pre[i] = u;
vis[i] = true;///标记节点
if(i==t) return true;///如果到达汇点,一条增广路径就找到了。
que.push(i);
}
}
}
return false;
}
int EK(int s,int t){
int ans = 0;
while(bfs(s,t)){
int d = MAX;
for(int i = t;i != s; i = pre[i])
d = min(d,mp[pre[i]][i]);///找出当前增广路径中最小的流量
for(int i = t;i != s; i = pre[i]){
mp[pre[i]][i] -= d;///正向边流量量更新
mp[i][pre[i]] += d;///反向边流量更新
}
ans += d;
}
return ans;
}
int main(){
int m,s,t;
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++) {
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
mp[x][y]+=z;
}
int ans = EK(s,t);
printf("%d\n",ans);
}
- 基于邻接表实现的EK算法:
#include<stdio.h>
#include<queue>
#include<string.h>
#include<algorithm>
using namespace std;
const int maxn = 1e5+10;
const int MAX = 0x3f3f3f3f;
int n,cnt,m;
bool vis[maxn];
int head[maxn];
struct Edge{
int v;
int w;
int nxt;
}edge[maxn];
void addEdge(int u,int v,int w){
edge[cnt].v = v;///cnt从0开始,
edge[cnt].w = w;
edge[cnt].nxt = head[u];
head[u] = cnt++;
}
struct Node{
int v;///存储当前边的起点
int id;///边的id
}pre[maxn];
void init(){
cnt = 0;
memset(edge,0,sizeof(edge));
memset(head,-1,sizeof(head));
}
bool bfs(int s,int t){
queue<int>que;
memset(vis,0,sizeof(vis));
memset(pre,-1,sizeof(pre));
pre[s].v = s;
vis[s] = true;
que.push(s);
while(!que.empty()){
int u = que.front();
que.pop();
for(int i = head[u]; i != -1; i=edge[i].nxt){
int v = edge[i].v;
if(!vis[v]&&edge[i].w){
pre[v].v = u;
pre[v].id = i;
vis[v] = true;
if(v==t) return true;///到达汇点
que.push(v);
}
}
}
return false;
}
int EK(int s,int t){
int ans = 0;
while(bfs(s,t)){
int d = MAX;
for(int i = t;i != s; i = pre[i].v)
d = min(d,edge[pre[i].id].w);
for(int i = t;i != s; i = pre[i].v){
edge[pre[i].id].w -= d;
edge[pre[i].id^1].w += d;
}
ans += d;
}
return ans;
}
int main(){
int m,s,t;
init();
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++) {
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
addEdge(x,y,z);
addEdge(y,x,0);
}
int ans = EK(s,t);
printf("%d\n",ans);
return 0;
}
1.2 Dinic 算法
Dinic算法的主要思想:
dinic在找增广路的时候也是找的最短增广路, 与 EK 算法不同的是dinic 算法并不是每次 bfs 只找一个增广路, 他会首先通过一次 bfs 为所有点添加一个标号, 构成一个层次图, 然后在层次图中通过dfs来寻找增广路进行更新。
看样例吧!!!
☞ 第一次调用bfs构建层次图:

第一次构建的层次图的第一条增广路径:路径上最小流量为3,整个网络的最大流量Maxflow =3,然后更新路径上每条边的流量。再然后2→4边的容量为0了。

第一次构建的层次图的第二条增广路径:路径上最小流量为4,整个网络的最大流量Maxflow =3+4,然后更新路径上每条边的流量。再然后3→5边的容量为0了。

到这里我们就发现找不到到汇点的增广路径了,这时候我们不需要再重建层次图找增广路径了。因为容量不达到上限的路径可以增广了。注意:先bfs层次后dfs,我们就可以快点找到离汇点较近的边,就能快速找到我们最大流量。这时我们在会看,是不是发现Dinic比EK效率高了很多。

#include<stdio.h>
#include<queue>
#include<string.h>
#include<algorithm>
using namespace std;
const int maxn = 200010;
const int INF = 0x3f3f3f3f;
int head[maxn];
int dis[maxn],cur[maxn];
int n,m,s,t,cnt;
struct Edge{
int v;
int w;
int nxt;
}edge[maxn];
void init(){
cnt = 0;
memset(edge,0,sizeof(edge));
memset(head,-1,sizeof(head));
}
void addEdge(int u,int v,int w){
edge[cnt].v = v;
edge[cnt].w = w;
edge[cnt].nxt = head[u];
head[u] = cnt++;
}
bool bfs(int s){
queue<int>que;
memset(dis,-1,sizeof(dis));
dis[s] = 0;
que.push(s);
while(!que.empty()){
int u = que.front();
que.pop();
for(int i = head[u]; i != -1; i=edge[i].nxt){
int v = edge[i].v;
if(dis[v]==-1&&edge[i].w){
dis[v] = dis[u]+1;///建立层次编号
que.push(v);
}
}
}
return dis[t]!=-1;
}
int dfs(int u,int flow){
if(u==t) return flow;
int detla = flow;///这个detla主要为了不直接传入参数flow,我们也可以直接传入
for(int i = cur[u]; i!=-1; i=edge[i].nxt){
cur[u] = edge[i].nxt;///
int v = edge[i].v;
if(dis[v]==dis[u]+1&&edge[i].w>0){
int d = dfs(v,min(detla,edge[i].w));///找出路径上权值最小的边
edge[i].w -= d;
edge[i^1].w += d;
detla -= d;
if(detla==0) break;
/*直接传入参数可以这样,直接返回
当前路径最小流量
如果这里没有返回,只能最后返回0了
if(d>0){
edge[i].w -= d;
edge[i^1].w += d;
return d;
}
*/
}
}
return flow - detla;
}
int dinic(){
int ans = 0;
while(bfs(s)){
for(int i=1; i<=n; i++) cur[i] = head[i];///初始化
ans += dfs(s,INF);
}
return ans;
}
int main(){
init();
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++) {
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
addEdge(x,y,z);
addEdge(y,x,0);
}
printf("%d\n",dinic());
return 0;
}
cur数组啥意思?我们知道head存储的是输入顺序同起点的边最后一条边的编号,如:按顺序输入1→2,1→4,1→3这三条边,head存储的是第三条边,然后通过nxt遍历其他边。我们的cur数组就是同起点的存储下一条边,也就不用每次都从head初始存储的边开始遍历。
- Dinic算法的时间复杂度:Dinic算法从源点到汇点建一次分层图,然后进行dfs,寻找增广路径,每次增广至少使分层图中的一条边容量为0,并且复杂度为O(增广路径长度)。当找不到增广路时再进行下一轮,由于每轮结束后源点到汇点不再连通,因此源点到汇点的最短路径增加1,最多有
O(n)轮;每轮每次增广至少使一条边消失,所以增广次数为O(m);每次增广最多经过n个顶点,所以其复杂度为O(n^2m)。





















 378
378











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








