HardStone512是一种基于双管道MD结构的密码杂凑算法，类似于SM3，用于信息摘要、完整性校验和数字签名。其特点是使用两个压缩函数PPPP和QQQQ并行处理消息块，增强抗碰撞和原像攻击能力。算法采用512bit消息分组，32步迭代，每步更新16个寄存器，结合Lai-Massey结构和S盒，提供良好的安全性。
基于双管道MD结构的密码杂凑算法HardStone512
黄金龙
HardStone512属于杂凑算法，与国产的SM3(杂凑算法)类似，都属于信息摘要算法，又被称为Hash算法，Hash算法主要用于完整性校验和提高数字签名的有效性，另外Hash算法也可用于消息鉴别码和随机数的生成。
常见的哈希算法结构为MD结构(MD5 SHA1 SHA256 SHA512 SM3 HAVAL等)、双管道MD结构(Grostl RIPEMD等)、宽管道结构(JH等)、HAIFA结构(BLAKE等) 、海绵结构(Keccak QUARK Photon等)。HardStone512算法采用双管道MD结构，它使用两个压缩函数PPPP和QQQQ并行对相同的消息块进行压缩运算，PPPP和QQQQ输出的杂凑值进入PPQQ，输出即为最终的杂凑值。
Hash算法的输入为任意长度的消息，输出为固定长度的Hash值，该输出就是散列值。通过给定的消息正向计算Hash值是简单的，但是通过Hash值逆向计算对应的消息是困难的。好的杂凑算法应该满足以下三点：
（1）抗碰撞攻击：已知消息M1的哈希值为H(M1)，找到另一消息M2(不等于M1)使得H(M1)=H(M2)是困难的。
（2）抗原像攻击：即对任意给定的Hash值H，找到满足H(M)=H的M在计算上是不可行的。
（3）抗第二原像攻击：找到两个不同的消息M1和M2使得H(M1)=H(M2)是困难的。
HardStone512算法的亮点
(1)对于同一个消息块，HardStone512使用两个不同的压缩函数PPPP和QQQQ对其进行压缩，这使得HardStone512算法抵抗碰撞攻击和原像攻击的能力大大增强。
(2)两个压缩函数的每一轮状态更新都使用到了全部的16个32位消息字，这使得算法的抗碰撞性大大增强，加上本算法使用S盒作为非线性部件，这使得模减差分分析和比特追踪法对本算法均已不再奏效。
(3)压缩函数中的轮函数使用Lai-Massey结构作为混淆扩散组件，这使得轮函数的扩散性好，同时使用Lai-Massey结构很容易构造满足双射特性的轮函数。
HardStone512密码杂凑算法描述
HardStone512算法采用了与Grostl相同的双管道MD结构，HardStone512的消息填充规则与SHA256一致，只是最大消息长度变为2的256次方Bit，同时没有消息扩展算法，压缩函数也不太一样。HardStone512压缩函数PPPP和QQQQ的每一轮更新全部16个寄存器的值，更新过程使用了全部的512Bit消息，也就是16个32位消息字。HardStone512密码杂凑算法的消息分组长度为512bit，摘要长度为512bit。压缩函数状态大小为512bit，共32步，每步更新全部16个寄存器，这加强了算法的雪崩效应。压缩函数采用了分组密码中的Lai-Massey结构，同时压缩函数的状态更新算法混合使用了模加运算和异或运算，这比单纯的使用模加运算或者异或运算更加复杂和安全。压缩函数为双射，这是为了保证输出杂凑值各比特的平衡性。
HardStone512密码杂凑算法的初始值
HardStone512密码杂凑算法的初始值IV共512bit，由16个32bit字(IV0∽IV15)串联而成，PPPP使用PIV，QQQQ使用QIV，具体值如下：
HardStone512密码杂凑算法的常量
HardStone512密码杂凑算法的常量为64个32bit字(CN0∽CN63)，具体值如下：
HardStone512密码杂凑算法的消息填充
对长度为l（l<2的256次方）比特的消息m，HardStone512密码杂凑算法首先将比特“1”添加到消息的末尾，再添加k个“0”，k是满足（l+k+1）=256Mod512的最小非负整数。然后再添加一个256位比特串，该比特串是消息长度的二进制表示。填充后的消息m`的长度是512 的倍数。
HardStone512密码杂凑算法的迭代压缩过程
将填充后的消息m`按512bit进行分组：m`=B(0)B(1)…B(n-1)，其中n=（l+k+257）/512。对m`按如下方式迭代：
FOR i=0 TO (n-1)
V(i+1)=CF(V(i)，M(i))
ENDFOR
其中CF是压缩函数，V(0)为512 bit初始值IV，B(i)为填充后的消息分组，迭代压缩的结果为V(n)。
MsgMix为消息混乱函数，描述如下：
FOR i=0 TO 15
M[i]=((B[i]⊞CN[4*i])⊕CN[4*i+1]⊞CN[4*i+2])⊕CN[4*i+3]；
ENDFOR
注意：这里的符号“⊕”表示逐比特异或运算，符号“⊞”表示模2的32次方加，“|”符号表示比特串的连接。
HardStone512密码杂凑算法的压缩函数PPPP
假定PH0，PH1，PH2，PH3，PH4，PH5，PH6，PH7，PH8，PH9，PH10，PH11，PH12，PH13，PH14，PH15为16个32位链接向量寄存器，M0，M1，M2，M3，M4，M5，M6，M7，M8，M9，M10，M11，M12，M13，M14，M15为16个32位消息字，T1，T2，T3，T4，TT1，TT2，TT3，TT4为中间变量，压缩函数PV(i+1)=PPPP(PV(i)，M(i))，PV(0)←PIV0||……||PIV15，0≤i≤n-1。
状态更新过程描述如下：
{
(M0|M1|M2|M3|M4|M5|M6|M7|M8|M9|M10|M11|M12|M13|M14|M15)←M(i)；
MsgMix(M，CN);
(PH0|PH1|PH2|PH3|PH4|PH5|PH6|PH7|PH8|PH9|PH10|PH11|PH12|PH13|PH14|PH15)←PV(i)；
FOR j=0 TO 31
T1=FFFF1(PH0，PH1，PH2，PH3)；
T2=FFFF2(PH4，PH5，PH6，PH7)；
T3=FFFF3(PH8，PH9，PH10，PH11)；
T4=FFFF4(PH12，PH13，PH14，PH15)；
TT1=(T1⊞T2)⊕T3⊞T4;
TT2=(T2⊞T3)⊕T4⊞T1;
TT3=(T3⊞T4)⊕T1⊞T2;
TT4=(T4⊞T1)⊕T2⊞T3;
PH0=PH0⊕T1⊕TT1⊞M0；
PH1=PH1⊕T1⊕TT1⊞M1；
PH2=PH2⊕T1⊕TT1⊞M2；
PH3=PH3⊕T1⊕TT1⊞M3；
PH4=PH4⊕T2⊕TT2⊞M4；
PH5=PH5⊕T2⊕TT2⊞M5；
PH6=PH6⊕T2⊕TT2⊞M6；
PH7=PH7⊕T2⊕TT2⊞M7；
PH8=PH8⊕T3⊕TT3⊞M8；
PH9=PH9⊕T3⊕TT3⊞M9；
PH10=PH10⊕T3⊕TT3⊞M10；
PH11=PH11⊕T3⊕TT3⊞M11；
PH12=PH12⊕T4⊕TT4⊞M12；
PH13=PH13⊕T4⊕TT4⊞M13；
PH14=PH14⊕T4⊕TT4⊞M14；
PH15=PH15⊕T4⊕TT4⊞M15；
Temp=PH0；PH0=PH1；PH1=PH2；PH2=PH3；PH3=PH4；PH4=PH5；PH5=PH6；PH6=PH7；PH7=PH8；PH8=PH9；PH9=PH10；PH10=PH11；
PH11=PH12；PH12=PH13；PH13=PH14；PH14=PH15；PH15 =Temp；
ENDFOR
PV(i+1)←(PH0|PH1|PH2|PH3|PH4|PH5|PH6|PH7|PH8|PH9|PH10|PH11
|PH12|PH13|PH14|PH15)⊕PV(i)
}
注意：这里的符号“⊕”表示逐比特异或运算，符号“⊞”表示模2的32次方加，“|”符号表示比特串的连接。
HardStone512密码杂凑算法的压缩函数QQQQ
假定QH0，QH1，QH2，QH3，QH4，QH5，QH6，QH7，QH8，QH9，QH10，QH11，QH12，QH13，QH14，QH15为16个32位链接向量寄存器，M0，M1，M2，M3，M4，M5，M6，M7，M8，M9，M10，M11，M12，M13，M14，M15为16个32位消息字，T1，T2，T3，T4，TT1，TT2，TT3，TT4为中间变量，压缩函数QV(i+1)=QQQQ(QV(i)，M(i))，QV(0)←QIV0||……||QIV15，0≤i≤n-1。
状态更新过程描述如下：
{
(M0|M1|M2|M3|M4|M5|M6|M7|M8|M9|M10|M11|M12|M13|M14|M15)←M(i)；
MsgMix(M，CN);
(QH0|QH1|QH2|QH3|QH4|QH5|QH6|QH7|QH8|QH9|QH10|QH11|QH12|QH13|QH14|QH15)←PV(i)；
FOR j=0 TO 31
T1=GGGG1(QH0，QH1，QH2，QH3)；
T2=GGGG2(QH4，QH5，QH6，QH7)；
T3=GGGG3(QH8，QH9，QH10，QH11)；
T4=GGGG4(QH12，QH13，QH14，QH15)；
TT1=(T1⊕T2⊞T3)⊕T4;
TT2=(T2⊕T3⊞T4)⊕T1;
TT3=(T3⊕T4⊞T1)⊕T2;
TT4=(T4⊕T1⊞T2)⊕T3;
QH0=(QH0⊞T1⊞TT1)⊕M0；
QH1=(QH1⊟T1⊟TT1)⊕M1；
QH2=(QH2⊞T1⊞TT1)⊕M2；
QH3=(QH3⊟T1⊟TT1)⊕M3；
QH4=(QH4⊞T2⊞TT2)⊕M4；
QH5=(QH5⊟T2⊟TT2)⊕M5；
QH6=(QH6⊞T2⊞TT2)⊕M6；
QH7=(QH7⊟T2⊟TT2)⊕M7；
QH8=(QH8⊞T3⊞TT3)⊕M8；
QH9=(QH9⊟T3⊟TT3)⊕M9；
QH10=(QH10⊞T3⊞TT3)⊕M10；
QH11=(QH11⊟T3⊟TT3)⊕M11；
QH12=(QH12⊞T4⊞TT4)⊕M12；
QH13=(QH13⊟T4⊟TT4)⊕M13；
QH14=(QH14⊞T4⊞TT4)⊕M14；
QH15=(QH15⊟T4⊟TT4)⊕M15；
Temp=QH0；QH0=QH1；QH1=QH2；QH2=QH3；QH3=QH4；QH4=QH5；QH5=QH6；QH6=QH7；QH7=QH8；QH8=QH9；QH9=QH10；QH10=QH11；
QH11=QH12；QH12=QH13；QH13=QH14；QH14=QH15；QH15 =Temp；
ENDFOR
QV(i+1)←(QH0|QH1|QH2|QH3|QH4|QH5|QH6|QH7|QH8|QH9|QH10|QH11|
QH12|QH13|QH14|QH15)⊕QV(i)
}
注意：这里的符号“⊕”表示逐比特异或运算，符号“⊞”表示模2的32次方加，“|”符号表示比特串的连接。
最终输出杂凑值为：Hash=PPQQ(PV(n)，QV(n))
{
(PV0|PV1|PV2|PV3|PV4|PV5|PV6|PV7|PV8|PV9|PV10|PV11|
PV12|PV13|PV14|PV15)= PV(n);
(QV0|QV1|QV2|QV3|QV4|QV5|QV6|QV7|QV8|QV9|QV10|QV11|
QV12|QV13|QV14|QV15)= QV(n);
(Hash0|Hash1|Hash2|Hash3|Hash4|Hash5|Hash6|Hash7|Hash8|Hash9|Hash10|Hash11|Hash12|Hash13|Hash14|Hash15)=Hash;
Hash0=PV0⊕QV0;
Hash1=PV1⊞QV1;
……
Hash14=PV14⊕QV14;
Hash15=PV15⊞QV15;
Hash=(Hash0|Hash1|Hash2|Hash3|Hash4|Hash5|Hash6|Hash7|Hash8|Hash9|
Hash10|Hash11|Hash12|Hash13|Hash14|Hash15);
}
PPPP使用的4个混淆扩散函数(FFFF1，FFFF2，FFFF3，FFFF4)
Y=FFFF1(X0，X1，X2，X3)
{
}
Y=FFFF2(X0，X1，X2，X3)
{
}
Y=FFFF3(X0，X1，X2，X3)
{
}
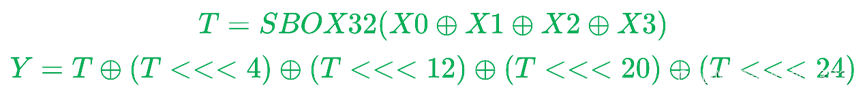
Y=FFFF4(X0，X1，X2，X3)
{
}
QQQQ使用的4个混淆扩散函数(GGGG1，GGGG2，GGGG3，GGGG4)
Y= GGGG1 (X0，X1，X2，X3)
{
}
Y= GGGG2 (X0，X1，X2，X3)
{
}
Y= GGGG3(X0，X1，X2，X3)
{
}
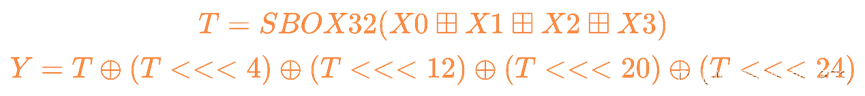
Y= GGGG4(X0，X1，X2，X3)
{
}
SBOX查找表
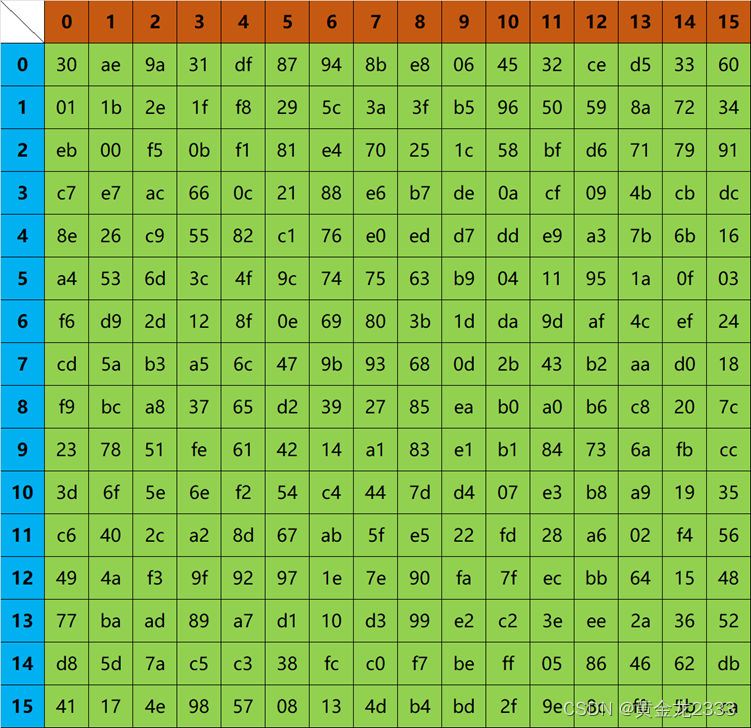
HardStone512密码杂凑算法的特点
HardStone512密码杂凑算法压缩函数整体结构为类分组密码结构，除了没有消息扩展函数外，还增加了多种新的设计技术，包括使用S盒作为非线性变换、使用了4个不同的加快雪崩效应的混淆扩散函数、每步使用全部16个32位消息字去更新16个寄存器的值等。压缩函数混合使用模加运算和异或运算，这样能够有效地抵抗碰撞攻击，使得模差分分析和比特追踪法难以奏效。使用双管道结构使得HardStone512能够有效抵抗原像攻击和第二原像攻击，这使得以往针对经典MD结构Hash算法的攻击方法均已不再奏效。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
