目录
3. 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
数据结构和算法本身解决的是“快”和“省”的问题,即如何让代码运行得更快,如何让代码更省存储空间。所以,执行效率是算法一个非常重要的考量指标。
为什么需要复杂度分析?
我把代码跑一遍,通过统计、监控,就能得到算法执行的时间和占用的内存大小。为什么还要做时间、空间复杂度分析呢?这种分析方法能比我实实在在跑一遍得到的数据更准确吗?
这种方法很准确。但是存在以下两个缺点:
1. 测试结果很依赖测试环境:测试环境中硬件的不同会对测试结果有很大的影响。
2. 测试结果受数据规模的影响很大 : 比如,对于小规模的数据排序,插入排序可能反倒会比快速排序要快。
所以,我们需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法。
大 O 复杂度表示法
那么,怎么粗略的进行估计一段代码的运行时间呢?来看一段简单的代码:
public int cal(int n)
{
int sum = 0;
for(int i = 0 ; i < n ; i++)
{
sum += i;
}
return sum;
}
可以假设每行代码执行的时间都一样,为 unit_time。
第3行和第8行都分别执行了1个unit_time。for循环一共两行,所以一共执行了2n个unit_time。
所以上面这个函数的执行时间为:(2n+2)*unit_time。
按照这个思路,再来观看下面这段代码:
int cal(int n)
{
int sum = 0;
int i = 1;
int j = 1;
for (; i <= n; ++i)
{
j = 1;
for (; j <= n; ++j)
{
sum = sum + i * j;
}
}
}最里面的for循环和总和的这两段一共执行的次数为2n^2。
最外边的for循环和j=1这两段代码一共执行的次数为2n。
上面3行初始化执行的次数为3。
所以T(n) = (2n^2+2n+3)*unit_time。
现在我们从中可以看出来,所有代码的执行时间 T(n) 与每行代码的执行次数成正比。
虽然我们不知道unit_time的具体的值,但是我们可以根据这个来总结一个规律。
T(n) = O(f(n))
1. T(n) 我们已经讲过了,它表示代码执行的时间;
2. n 表示数据规模的大小;
3. f(n) 表示每行代码执行的次数总和。因为这是一个公式,所以用 f(n) 来表示。
4. 公式中的 O,表示代码的执行时间 T(n) 与 f(n) 表达式成正比。
所以,第一个例子中的 T(n) = O(2n + 2),第二个例子中的 T(n) = O(2n^2 + 2n + 3)。
这就是大 O 时间复杂度表示法。大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度(asymptotic time complexity),简称时间复杂度。
当 n 很大时,你可以把它想象成 10000、100000。而公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以了。
如果用大 O 表示法表示刚讲的那两段代码的时间复杂度,就可以记为:T(n) = O(n); T(n) = O(n^2)。
时间复杂度分析
根据上面代码的分析。我们现在可以得出一个规律。
1. 只关注循环执行次数最多的一段代码
大 O 这种复杂度表示方法只是表示一种变化趋势。我们通常会忽略掉公式中的常量、低阶、系数,只需要记录一个最大阶的量级就可以了。所以,我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那一段代码就可以了。
就比如刚才第一段代码。它的时间复杂度为O(n)。
第二段代码。它的时间复杂度为O(n^2)。
2. 加法法则:总复杂度等于量级最大的那段代码的复杂度
分析下面的代码:
int cal(int n) {
int sum_1 = 0;
int p = 1;
for (; p < 100; ++p) {
sum_1 = sum_1 + p;
}
int sum_2 = 0;
int q = 1;
for (; q < n; ++q) {
sum_2 = sum_2 + q;
}
int sum_3 = 0;
int i = 1;
int j = 1;
for (; i <= n; ++i) {
j = 1;
for (; j <= n; ++j) {
sum_3 = sum_3 + i * j;
}
}
return sum_1 + sum_2 + sum_3;
}
这个代码分为三部分,分别是求 sum_1、sum_2、sum_3。
我们可以分别分析每一部分的时间复杂度,然后把它们放到一块儿,再取一个量级最大的作为整段代码的复杂度。
第一段的时间复杂度是多少呢?这段代码循环执行了 100 次,所以是一个常量的执行时间,跟 n 的规模无关。
这里再强调一下,即便这段代码循环 10000 次、100000 次,只要是一个已知的数,跟 n 无关,照样也是常量级的执行时间。当 n 无限大的时候,就可以忽略。尽管对代码的执行时间会有很大影响,但是回到时间复杂度的概念来说,它表示的是一个算法执行效率与数据规模增长的变化趋势,所以不管常量的执行时间多大,我们都可以忽略掉。因为它本身对增长趋势并没有影响。
那第二段代码和第三段代码的时间复杂度是多少呢?答案是 O(n) 和 O(n^2)。
综合这三段代码的时间复杂度,我们取其中最大的量级。
所以,整段代码的时间复杂度就为 O(n2)。也就是说:总的时间复杂度就等于量级最大的那段代码的时间复杂度。
那我们将这个规律抽象成公式就是:
如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n)))。
3. 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
通过下面的例子你就能清楚了,跟加法法则同一个道理。
int cal(int n) {
int ret = 0;
int i = 1;
for (; i < n; ++i) {
ret = ret + f(i);
}
}
int f(int n) {
int sum = 0;
int i = 1;
for (; i < n; ++i) {
sum = sum + i;
}
return sum;
}我们单独看 cal() 函数。假设 f() 只是一个普通的操作,那第 4~6 行的时间复杂度就是,T1(n) = O(n)。
但 f() 函数本身不是一个简单的操作,它的时间复杂度是 T2(n) = O(n)。
所以,整个 cal() 函数的时间复杂度就是,T(n) = T1(n) * T2(n) = O(n*n) = O(n2)。
几种常见时间复杂度实例分析
虽然代码千差万别,但是常见的复杂度量级并不多。
下面复杂度量级几乎涵盖了你今后可以接触的所有代码的复杂度量级。

对于刚罗列的复杂度量级,我们可以粗略地分为两类,多项式量级和非多项式量级。
其中,非多项式量级只有两个:O(2^n) 和 O(n!)。
当数据规模 n 越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长。所以,非多项式时间复杂度的算法其实是非常低效的算法。这里就不进行讲解,知道有这回事儿就行了。
1. O(1)
O(1) 只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。比如这段代码,即便有 3 行,它的时间复杂度也是 O(1),而不是 O(3)。
int i = 8;
int j = 6;
int sum = i + j;只要代码的执行时间不随 n 的增大而增长,这样代码的时间复杂度我们都记作 O(1)。或者说,
一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
2.O(logn)、O(nlogn)
对数阶时间复杂度非常常见,同时也是最难分析的一种时间复杂度。通过一个例子来说明一下。
int i = 1;
while (i < n) {
i = i * 2;
}根据我们前面讲的复杂度分析方法,第三行代码是循环执行次数最多的。所以,我们只要能计算出这行代码被执行了多少次,就能知道整段代码的时间复杂度。这里需要用到高中的数学知识点,看我分析一下你就明白了。
假设n=4,这段代码就只执行两次。2^2 =4;
假设n=8,这段代码就只执行了3次。 2^3 = 8;
……
最后假设n为未知数,刚好是2的x次方。是不是就是2^x = n;执行了x次。 即x = log2(底数为2) n
变量 i 的值从 1 开始取,每循环一次就乘以 2。当大于 n 时,循环结束。还记得我们高中学过的等比数列吗?实际上,变量 i 的取值就是一个等比数列。如果我把它一个一个列出来,就应该是这个样子的:

所以,我们只要知道 x 值是多少,就知道这行代码执行的次数了。通过 2x=n 求解 x 这个问题我们想高中应该就学过了,我就不多说了。x=log2(底数为2) n,所以,这段代码的时间复杂度就是 O(log2(底数为2) n)。
现在,我把代码稍微改下,你再看看,这段代码的时间复杂度是多少?
int i=1;
while (i <= n) {
i = i * 3;
}实际上,不管是以 2 为底、以 3 为底,还是以 10 为底,我们可以把所有对数阶的时间复杂度都记为 O(logn)。为什么呢?
我们知道,对数之间是可以互相转换的。
根据对数的换底公式:
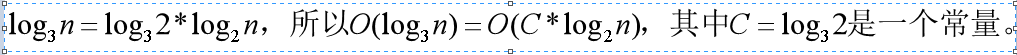
基于我们前面的一个理论:在采用大 O 标记复杂度的时候,可以忽略系数,即 O(Cf(n)) = O(f(n))。所以,O(log2n) 就等于 O(log3n)。因此,在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为 O(logn)。
如果你理解了我前面讲的 O(logn),那 O(nlogn) 就很容易理解了。还记得我们刚讲的乘法法则吗?如果一段代码的时间复杂度是 O(logn),我们循环执行 n 遍,时间复杂度就是 O(nlogn) 了。而且,O(nlogn) 也是一种非常常见的算法时间复杂度。比如,归并排序、快速排序的时间复杂度都是 O(nlogn)。
3. O(m+n)、O(m*n)
我们再来讲一种跟前面都不一样的时间复杂度,代码的复杂度由两个数据的规模来决定。老规矩,先看代码!
int cal(int m, int n) {
int sum_1 = 0;
int i = 1;
for (; i < m; ++i) {
sum_1 = sum_1 + i;
}
int sum_2 = 0;
int j = 1;
for (; j < n; ++j) {
sum_2 = sum_2 + j;
}
return sum_1 + sum_2;
}从代码中可以看出,m 和 n 是表示两个数据规模。我们无法事先评估 m 和 n 谁的量级大,所以我们在表示复杂度的时候,就不能简单地利用加法法则,省略掉其中一个。所以,上面代码的时间复杂度就是 O(m+n)。
针对这种情况,原来的加法法则就不正确了,我们需要将加法规则改为:T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效:T1(m)*T2(n) = O(f(m) * f(n))。
总结:
一、什么是复杂度分析?
1.数据结构和算法解决是“如何让计算机更快时间、更省空间的解决问题”。
2.因此需从执行时间和占用空间两个维度来评估数据结构和算法的性能。
3.分别用时间复杂度和空间复杂度两个概念来描述性能问题,二者统称为复杂度。
4.复杂度描述的是算法执行时间(或占用空间)与数据规模的增长关系。
二、为什么要进行复杂度分析?
1.和性能测试相比,复杂度分析有不依赖执行环境、成本低、效率高、易操作、指导性强的特点。
2.掌握复杂度分析,将能编写出性能更优的代码,有利于降低系统开发和维护成本。
三、如何进行复杂度分析?
1.大O表示法
1)来源
算法的执行时间与每行代码的执行次数成正比,用T(n) = O(f(n))表示,其中T(n)表示算法执行总时间,f(n)表示每行代码执行总次数,而n往往表示数据的规模。
2)特点
以时间复杂度为例,由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势,所以常量阶、低阶以及系数实际上对这种增长趋势不产决定性影响,所以在做时间复杂度分析时忽略这些项。
2.复杂度分析法则
1)单段代码看高频:比如循环。
2)多段代码取最大:比如一段代码中有单循环和多重循环,那么取多重循环的复杂度。
3)嵌套代码求乘积:比如递归、多重循环等
4)多个规模求加法:比如方法有两个参数控制两个循环的次数,那么这时就取二者复杂度相加。
四、常用的复杂度级别?
多项式阶:随着数据规模的增长,算法的执行时间和空间占用,按照多项式的比例增长。包括,
O(1)(常数阶)、O(logn)(对数阶)、O(n)(线性阶)、O(nlogn)(线性对数阶)、O(n^2)(平方阶)、O(n^3)(立方阶)
非多项式阶:随着数据规模的增长,算法的执行时间和空间占用暴增,这类算法性能极差。包括,
O(2^n)(指数阶)、O(n!)(阶乘阶)
常用的复杂度级别?
多项式阶:随着数据规模的增长,算法的执行时间和空间占用,按照多项式的比例增长。包括,
O(1)(常数阶)、O(logn)(对数阶)、O(n)(线性阶)、O(nlogn)(线性对数阶)、O(n^2)(平方阶)、O(n^3)(立方阶)
非多项式阶:随着数据规模的增长,算法的执行时间和空间占用暴增,这类算法性能极差。包括,
O(2^n)(指数阶)、O(n!)(阶乘阶

以上内容学自:极客时间--王争老师的课《数据结构与算法之美》。感觉写的极好,跟各位小伙伴分享一下。
https://time.geekbang.org/column/article/40036






















 2020
2020











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








