HyperWorks进阶教程：OptiStruct相关函数与功率谱和随机响应分析

相关柔数措述的是一个时间序列与另一个时间序列的相关程度。例如、正弦函数曲线沿时合平彩相大周期以后与原丽数完全相同、而平移0.5个周期后则与原函数完全相反。相关商数的断播述的便是这一变化，它是时间延迟7的函数。相关函数分为自相关函数与互相关函数两类。

（1）自相关函数：用于描述信号x()自身在发生时延后的相关性。

（2）互相关函数：用于描述两个信号x()与y(t)在发生时延后的相关性。

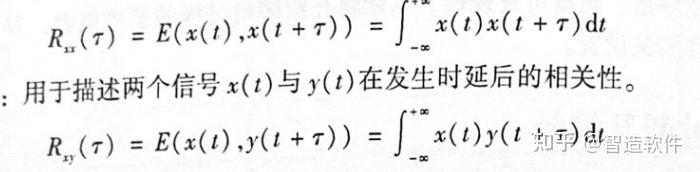
随机信号的一个重要统计特性是功率谱，它是信号在频域能量分布的统计曲线，与相关函数为拉普拉斯变换对。对于时域随机信号x(1)，它的自功率谱函数S.(ω)即傅里叶频谱x(∞)幅值*平方。

对式(8-8)及式(89)进行拉普拉斯变换，可以得到自相关函数R(7)与自功率谱S.(w)满足拉普拉斯变换对的关系，互相关函数R。(7)与互功率谱S,(w)也满足拉普拉斯变换对的关系。

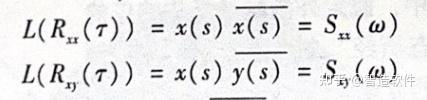
式中，s=jo;x(s)与y(s)表示信号的频响曲线;()表示取共轭复数对特别情况下，随机信号的自相关函数仅在r为0时为常数σ’，其余时刻均为0;相应的随机信号自功率谱为

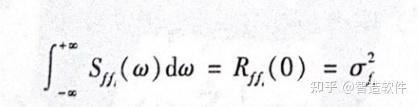
对于一般的随机激励￡(1)及人(1)，它们的互相关函数与互功率谱通常是不为零的，仅当随激励,(1)及6(1)是相互独立(不相关)的情况下，互相关或互功率谱才为零。

R(T)≠0,S (ω)≠0

Optistruct中的随机激励功率谱采用RANDPS卡片进行定义。一般来说，随机激励功率谱由试验标准定义或由实测的时域激励曲线通过式(8-11)及式(8-12)生成。如果随机激励包含多个自由度(多节点或多方向)，那么需要定义每个自由度上的自功率谱以及所有自由度之间的互功谱。另外，工程应用中的频谱及功率谱曲线一般定义在正频率范围，即采用单边谱输人方式：

在Optistruct随机响应分析中，要求输人的功率谱全部为单边谱G,(ω)或全部为双边谱S(ω)。如果功率谱输入采用单边谱，那么输出的响应为单边谱;如果功率谱输人为双边谱，那么输出的响应为双边谱。

本篇内容取自HyperWorks进阶教程系列的《OptiStruct结构分析与工程应用》，版权归原作者所有，如有侵犯您的权益，请及时联系我们，我们将立即删除。