二分搜索—— 完全二叉树统计节点个数

注意：做2的幂时不要用Math.pow，这样会超时。用1<< a 这个方法来得到2的a次幂！！！

参考：

http://blog.csdn.net/freeelinux/article/details/53679708（二分法，C++）

http://www.cnblogs.com/grandyang/p/4567827.html （递归）

【题目】

题目链接：https://leetcode.com/problems/count-complete-tree-nodes/#/description

给定一棵完全二叉树的根节点root，返回这棵树的节点个数。如果完全二叉树的节点数为N，请实现时间复杂度低于O(N)的解法。
给定树的根结点root，请返回树的大小。

思路：

计算完全二叉树最左节点的位置，目的是计算出二叉树的高度，然后再找到右子树的最左节点的位置与之做比较，则有以下两种情况：

1）  如果右子树的最左节点刚好到达最下面的一层的话（如下图），那么说明该树的左子树是一颗满二叉树，那么可以根据二叉树的性质计算出左子树的节点个数，再加上根节点，剩下需要计算的就是右子树的个数了，采用递归的方式。

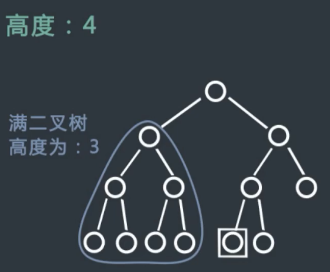
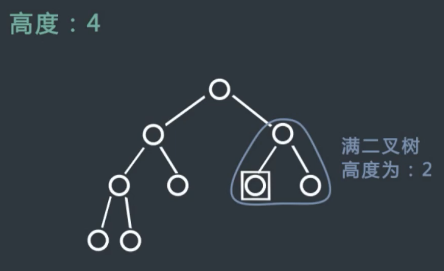
2） 如果右子树的最左节点不能到达最下面的一层的话（如下图），说明右子树也是一颗满二叉树，只是层数少了，同理，根据二叉树的性质计算出右子树的节点个数，再加上根节点的，剩下的只需计算左子树节点个数，同样采用递归方式。

这种方式的复杂度肯定比遍历的复杂度低。

遍历的方式，时间复杂度是O(N)

采用这种方式，时间复杂度为O((logN)^2)，即二叉树高度的平方。

其实这种方法的思想是二分思想，其实就是在看完全二叉树最后一层的最右节点到底处在什么样的位置上。

public class CountCompleteBinaryTreeNodes {
	
	class TreeNode{
		int val;
		TreeNode left=null;
		TreeNode right=null;
		public void Node(int val){
			this.val=val;
		}
	}
	
	//计算完全二叉树的层数
	public int getDepth(TreeNode root){
		if(root==null)
			return 0;
		int dep=1;
		while(root.left!=null){
			root=root.left;
			dep++;
		}
		return dep;
	}
	
	//统计完全二叉树的节点个数
	public int countNodes(TreeNode root){
		
		if(root==null)
			return 0;
		else if(root.left==null&&root.right==null)
			return 1;
		
		int left_left_level=getDepth(root);  //根节点左子树最左节点的层数
		int right_left_level=0;  //根节点右子树最左节点的层数
		
		if(root.right!=null){
			right_left_level=getDepth(root.right);
		}
		right_left_level++;  //加上根节点原本的一层
		if(left_left_level==right_left_level){
			return (1<<(right_left_level-1))+countNodes(root.right);
		}
		else{  //left_left_level > right_left_level
			return (1<<(right_left_level-1))+countNodes(root.left);
		}
	}
	
}