归并排序和快速排序

一、归并排序

排序算法稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

1、归并排序是稳定的排序算法

归并排序稳不稳定关键在于merge函数。在合并过程中，如果A[p..q]和A[q+1...r]之间有值相同元素，先把A[p...q]中的元素放入tmp数组。这样就保证了值相同的元素，在合并的先后顺序不变

归并处理过程由下到上，先处理子问题，在合并

2.时间复杂度 O(nlogn)

递归代码的时间复杂度可以写成递推公式。

(1)假设对n个元素规定需要的时间是T(n)，分解成两个子数组排序的时间T(n/2)

(2)merge函数时间复杂度O(n)

归并排序的时间复杂度计算公式：

T(1) = C; n = 1,只需要常量级的执行时间C

T(n)=2*T(n/2) + n; n > 1

进一步分解得出结论，得出结论T(n)=2^kT(n/2^k) +kn，当T(n/2^k)=T(1)时，就是n/2^k得到k=log2(n)，带入公式得到，T(n)=Cn+nlog2n

时间复杂度稳定，最好最坏，平均都是O(nlogn)

3.空间复杂度O(n)

在任意时刻，CPU只会有一个函数在执行，只会有一个临时的内存在使用。临时内存空间最大不会超过n个数据大小

4.缺点

（1）不是原地排序算法，merge函数需要借助额外存储空间

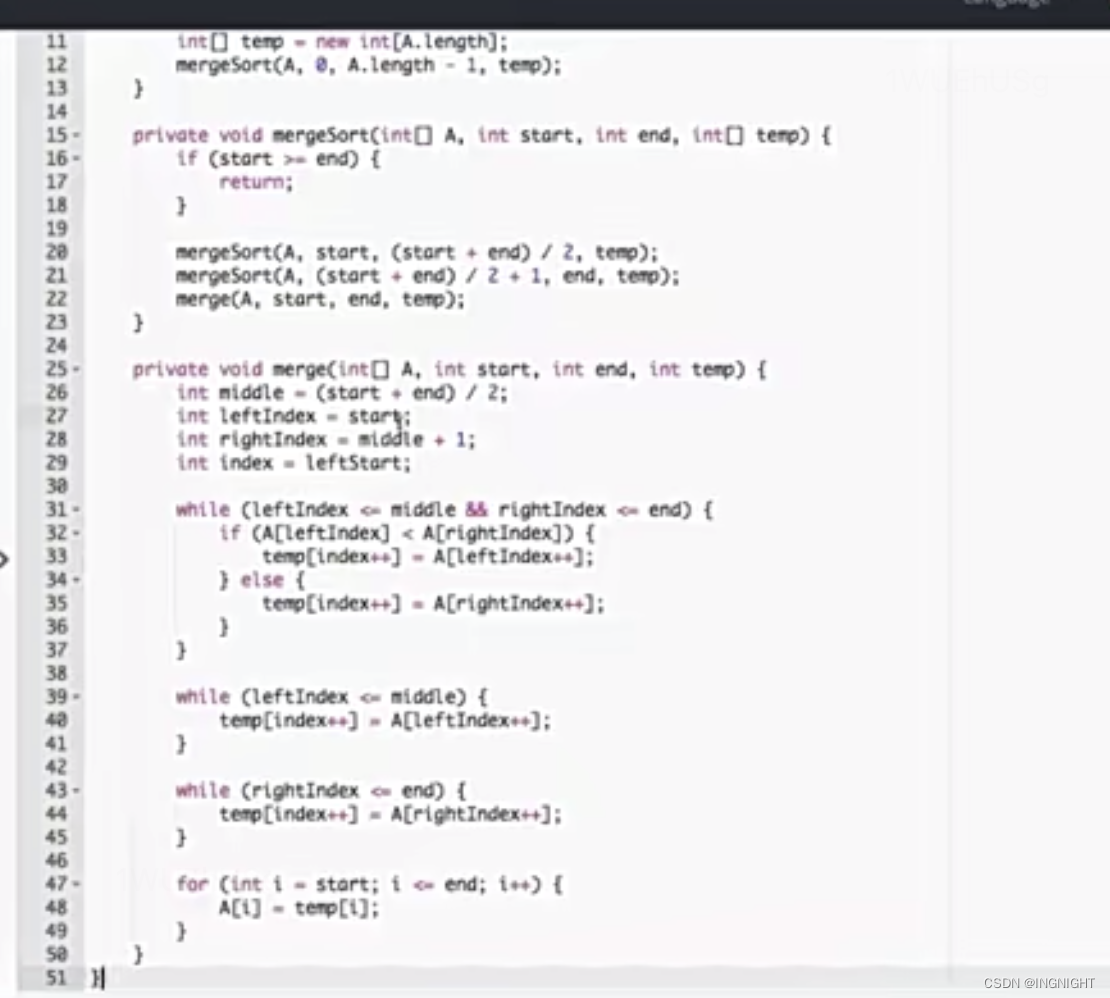
先局部有序，然后在整体有序

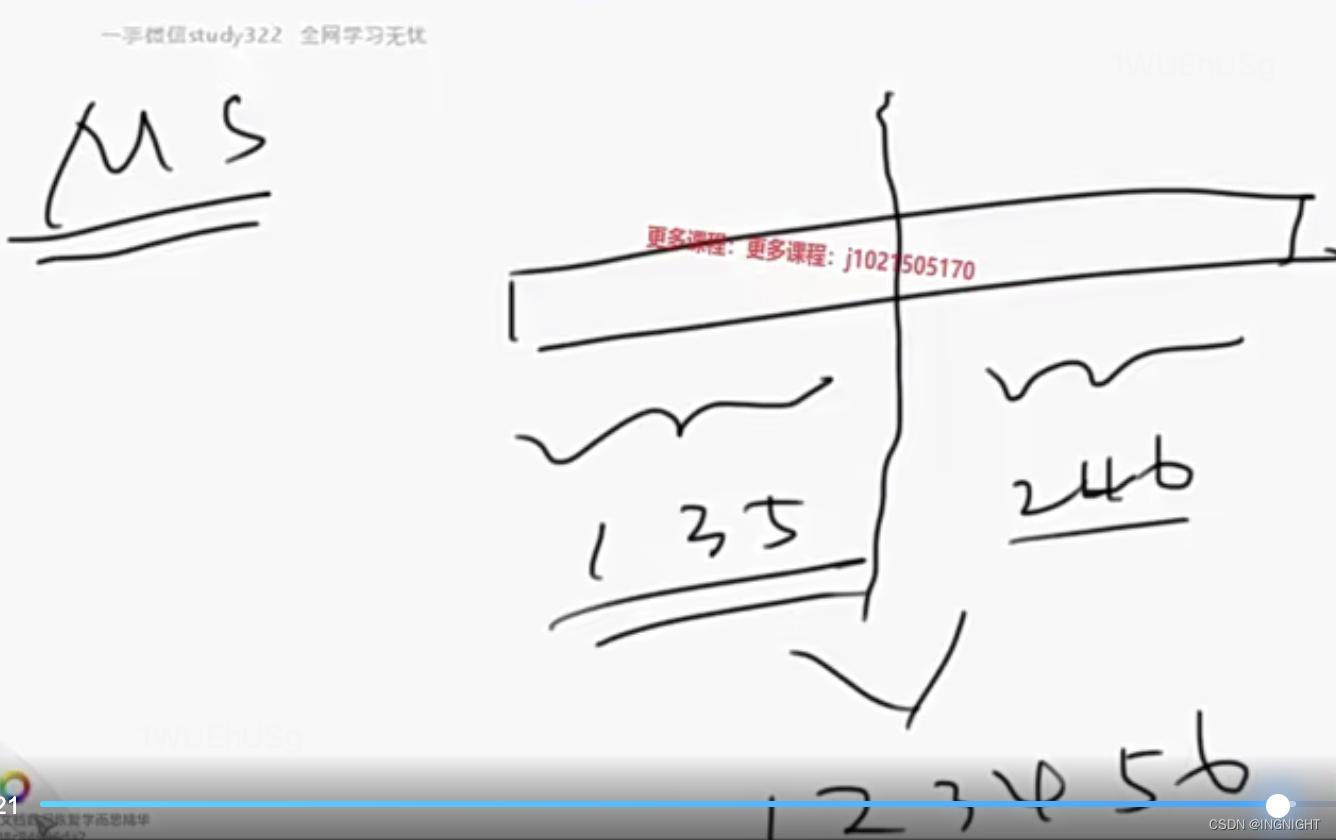
二、快速排序

1.快速排序是原地、不稳定的排序算法

代码：快速排序代码实现_INGNIGHT的博客-CSDN博客

比如数组：6,5,6,3,4，经过第一次分区之后，两个6的顺序会有改变。（选取下表最高的值4为pivot）

快排处理过程由上到下，先分区，在处理子问题。原地排序，解决归并排序占用过多内存问题。

2.时间复杂度 O(nlogn)

3.空间复杂度O(1)

4.缺点

(1)每次分区操作，选择的pivot都很合适，正好能将大区间对等一分为二。原数据已经有序，1,3,5,6,8，每次选取最后一个元素作为pivot，每次分区得到的两个区间都是不均等的，需要进行大约n次分区操作。每次分区平均扫面大约n/2个元素，这是快排时间复杂度退化为O(n^2)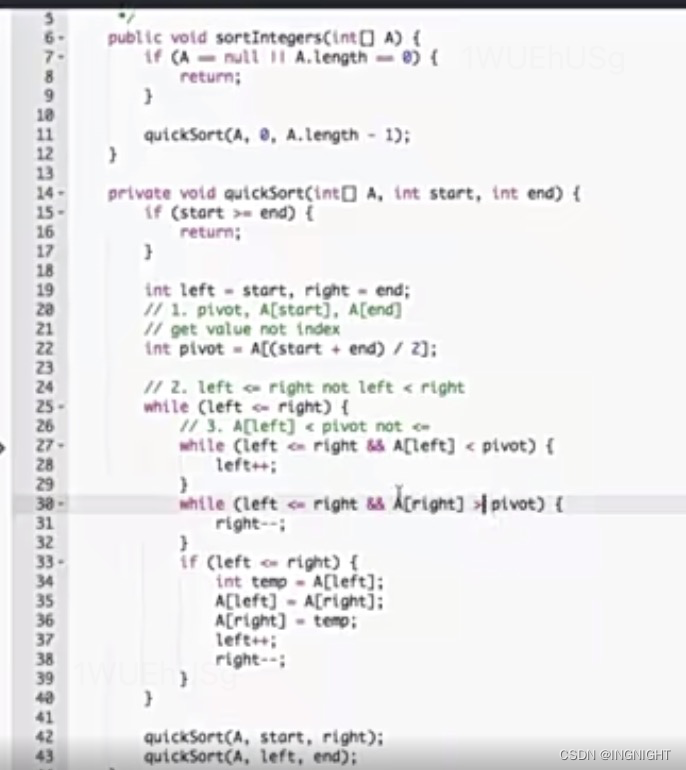

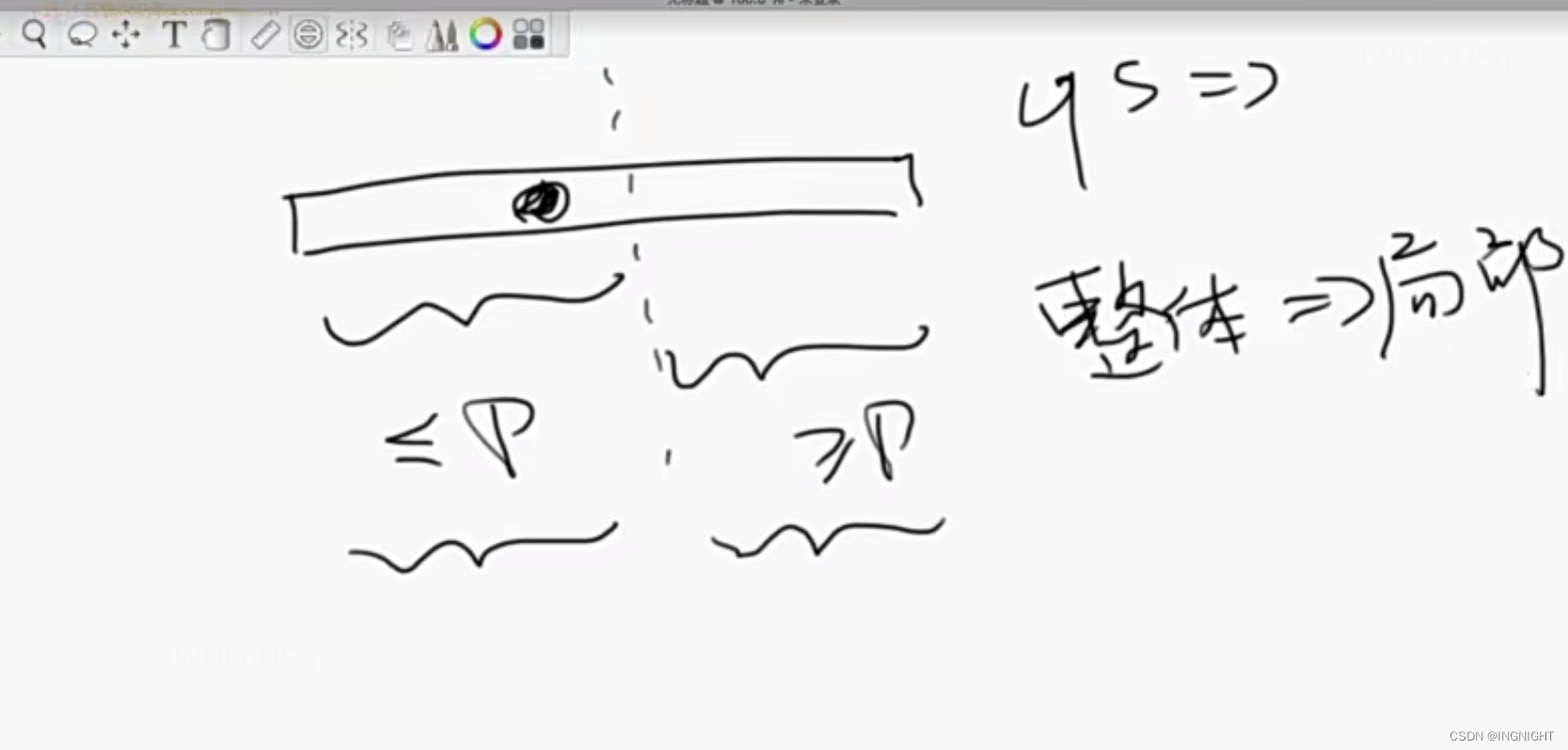
 先整体有序，在局部有序

题目：

https://blog.csdn.net/INGNIGHT/article/details/131625238

215. 数组中的第K个最大元素-CSDN博客

12 | 排序（下）：如何用快排思想在O(n)内查找第K大元素？归并排序和快速排序-CSDN博客

algo/c-cpp/12_sorts/quick_sort.c at master · wangzheng0822/algo · GitHub

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
    quick_sort(nums, 0, nums.size()-1);
    return nums;
    }
 private:
    void quick_sort(std::vector<int>& nums, int start, int end) {
    if (start >= end) {
        return;
    }
    int index = partition(nums, start, end);
    quick_sort(nums, start, index-1);
    quick_sort(nums, index+1, end);
    }
    int partition(std::vector<int>& nums, int start, int end) {
    int left = start;
    int right = end;
    swap(nums[start], nums[(start+end)/2]);
    ++left;
    while (left <= right) {
        while(left <= right && nums[left] < nums[start]) {
        ++left;
        }
        while(left <= right && nums[right] > nums[start]) {
        --right;
        }
        if (left <= right) {
        swap(nums[left], nums[right]);
        ++left;
        --right;
        }
    }
    swap(nums[start], nums[right]);
    return right;
    }
};

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        if (nums.size() <= 0) {
            return nums;
        }
        quick_sort(nums, 0, nums.size()-1);
        return nums;
    }
private:
    void quick_sort(std::vector<int>& nums, int left, int right) {
        if (left >= right) {
            return;
        }
        int mid = partition(nums, left, right);
        // mid然后的右边区间起始点
        quick_sort(nums, left, mid-1);
        quick_sort(nums, mid, right);
    }
    int partition(std::vector<int>& nums, int left, int right) {
 
        int index = random() %(right-left+1);
        swap(nums[left], nums[left+index]);
        int val = nums[left];
        // 和val相等的元素均匀的分布在左右两边
        while (left <= right) {
            while (left <= right && nums[left] < val ) {
                ++left;
            }
            while (left <= right && nums[right] > val) {
                --right;
            }
            // 两个和val相等的元素也会进行交换
            if (left <= right) {
                swap(nums[left], nums[right]);
                ++left;
                --right;
            }
        }
        // 此时left一定是在right的右边
        return left;
    }
};

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        if (nums.size() <= 0) {
            return nums;
        }
        quick_sort(nums, 0, nums.size()-1);
        return nums;
    }
private:
    void quick_sort(std::vector<int>& nums, int left, int right) {
        if (left >= right) {
            return;
        }
        std::pair<int, int> mid = partition(nums, left, right);
        // mid然后的右边区间起始点
        quick_sort(nums, left, mid.second);
        quick_sort(nums, mid.first, right);
    }
    std::pair<int, int> partition(std::vector<int>& nums, int left, int right) {
 
        int index = random() %(right-left+1);
        swap(nums[left], nums[left+index]);
        int val = nums[left];
        // 和val相等的元素均匀的分布在左右两边
        while (left <= right) {
            while (left <= right && nums[left] < val ) {
                ++left;
            }
            while (left <= right && nums[right] > val) {
                --right;
            }
            // 两个和val相等的元素也会进行交换
            if (left <= right) {
                swap(nums[left], nums[right]);
                ++left;
                --right;
            }
        }
        // 此时left一定是在right的右边
        return std::pair<int, int>(left, right);
    }
};