Algorithm S
Algorithm S (Straight two-way merge sort). Records R1,… ,RN are sorted
using two memory areas as in Algorithm N.
S1. [Initialize.] Set s <– 0, p <– 1. (For the significance of variables s, i, j, k,
I, and d, see Algorithm N. Here p represents the size of ascending runs to
be merged on the current pass; further variables q and r will keep track of
the number of unmerged items in a run.)
S2. [Prepare for pass.] If s = 0, set i <– 1, j <– N, k <– N, I <– 2N+1; if s = 1,
set i <– N+1, j <– 2N, k <– 0, I <– N+1. Then set d <– 1, q <– p, r <– p.
S3. [Compare Ki:Kj] If Ki > Kj, go to step S8.
S4. [Transmit Ri.] Set k <– k+d, Rk <– Ri.
S5. [End of run?] Set i <– i+1, q <– q-1. If q > 0, go back to step S3.
S6. [Transmit Rj.] Set k <– k+d. Then if k = I, go to step S13; otherwise set
Rk <– Rj.
S7. [End of run?] Set j <– j-1, r <– r-1. If r > 0, go back to step S6;
otherwise go to S12.
S8. [Transmit Rj.] Set k <– k+d, Rk <– Rj.
S9. [End of run?] Set j <– j-1, r <– r-1. If r > 0, go back to step S3.
S10. [Transmit Ri.] Set k <– k+d. Then if k = I, go to step S13; otherwise set
Rk <– Ri .
S11. [End of run?] Set i <– i+1, q <– q-1. If q > 0, go back to step S10.
S12. [Switch sides.] Set q <– p, r <– p, d <– -d, and interchange k <–> I. If
j-i < p, return to step S10; otherwise return to S3.
S13. [Switch areas.] Set p <– p+p. If p < N, set s <– 1-s and return to S2.
Otherwise sorting is complete; if s = 0, set
(R1, … , RN) <– (RN+1, … , R2N).
(The latter copying operation will be done if and only if ceil(lgN) is odd,
regardless of the distribution of the input. Therefore it is possible to predict
the location of the sorted output in advance, and copying will usually be
unnecessary.) |
Flow diagram
Almost the same with Natural two-way merge sort.
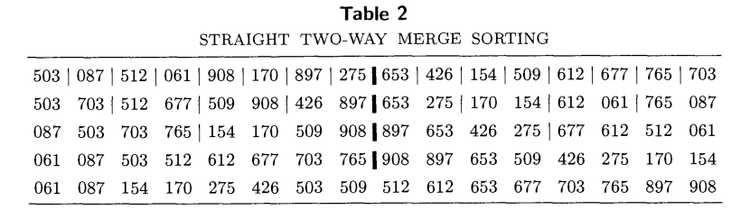
Data table
Java program
In this program, R1,…,RN were simplified to K1,…,KN.
/**
* Created with IntelliJ IDEA.
* User: 1O1O
* Date: 12/3/13
* Time: 10:01 PM
* :)~
* Straight Two-way Merge Sort:Sorting by Merging:Internal Sorting
*/
public class Main {
public static void main(String[] args) {
int N = 16;
int[] K = new int[33];
int temp;
/*Prepare the data*/
K[1] = 503;
K[2] = 87;
K[3] = 512;
K[4] = 61;
K[5] = 908;
K[6] = 170;
K[7] = 897;
K[8] = 275;
K[9] = 653;
K[10] = 426;
K[11] = 154;
K[12] = 509;
K[13] = 612;
K[14] = 677;
K[15] = 765;
K[16] = 703;
/*Output unsorted Ks*/
System.out.println("Unsorted Ks:");
for(int i=1; i<=N; i++){
System.out.println(i+":"+K[i]);
}
System.out.println();
/*Kernel of the Algorithm!*/
int s = 0;
int p = 1;
int i = -1;
int j = -1;
int k = -1;
int l = -1;
int d;
int q;
int r;
do{ /*S2*/
if(s == 0){
i = 1;
j = N;
k = N;
l = 2*N+1;
}else if(s == 1){
i = N+1;
j = 2*N;
k = 0;
l = N+1;
}
d = 1;
q = p;
r = p;
do{ /*S3*/
if(K[i] > K[j]){
k += d; /*S8*/
K[k] = K[j];
j--; /*S9*/
r--;
if(r > 0){
continue;
}else {
do{
do{
k += d; /*S10*/
if(k == l){
break;
}else {
K[k] = K[i];
}
i++; /*S11*/
q--;
}while (q > 0);
if(k == l){
break;
}
q = p; /*S12*/
r = p;
d = -d;
temp = k;
k = l;
l = temp;
}while (j-i < p);
if(k == l){
break;
}
}
}else {
k += d; /*S4*/
K[k] = K[i];
i++; /*S5*/
q--;
if(q > 0){
continue;
}else {
do{
do{
k += d; /*S6*/
if(k == l){
break;
}else {
K[k] = K[j];
}
j--; /*S7*/
r--;
}while (r > 0);
if(k == l){
break;
}
q = p; /*S12*/
r = p;
d = -d;
temp = k;
k = l;
l = temp;
}while (j-i < p);
if(k == l){
break;
}
}
}
}while (true);
p = p + p; /*S13*/
if(p < N){
s = 1 - s;
}
}while (p < N);
if(s == 0){
for(int m=1; m<=N; m++){
K[m] = K[N+m];
}
}
/*Output sorted Ks*/
System.out.println("Sorted Ks:");
for(int m=1; m<=N; m++){
System.out.println(m+":"+K[m]);
}
}
}Outputs
Unsorted Ks:
1:503
2:87
3:512
4:61
5:908
6:170
7:897
8:275
9:653
10:426
11:154
12:509
13:612
14:677
15:765
16:703
Sorted Ks:
1:61
2:87
3:154
4:170
5:275
6:426
7:503
8:509
9:512
10:612
11:653
12:677
13:703
14:765
15:897
16:908Reference
<< The art of computer programming: Sorting and Searching >> VOLUME 3, DONALD E. KNUTH























 1124
1124

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








