文章中内容与图片大部分来自Reference,本文只是以方便自己理解的方式进行整理。
格雷码
在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同且最高位与最低位也只有一位二进制数不同, 则称这种编码为格雷码(Gray Code)
普通二进制码转换成格雷码
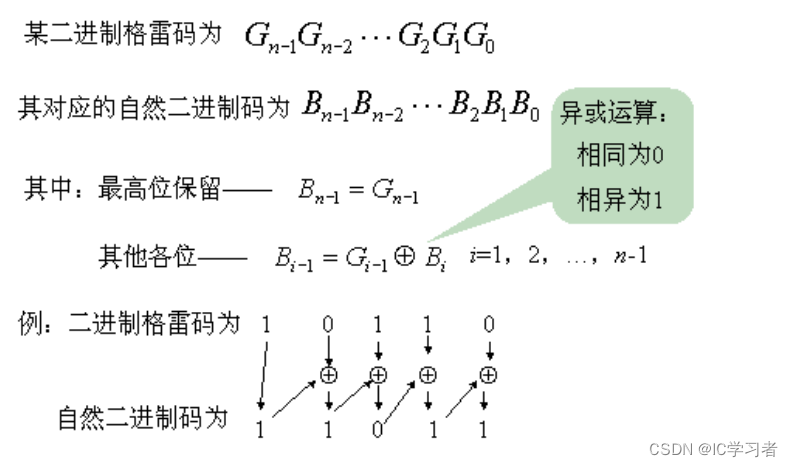
二进制码转换成二进制格雷码,其法则是保留二进制码的最高位作为格雷码的最高位,而次高位格雷码为二进制码的高位与次高位相异或,而格雷码其余各位与次高位的求法相类似。


经过简单验证,1010->1111,没毛病
但是如果格雷码只是从0变到10呢?
从10回到0,便是四个二进制位都需要变化
格雷码转换成普通二进制码
二进制格雷码转换成二进制码,其法则是保留格雷码的最高位作为自然二进制码的最高位,而次高位自然二进制码为高位自然二进制码与次高位格雷码相异或。

以1010为例,1010->1100,没毛病
进一步
如果编码从末尾变到开头,如从10变到0
对应的是1111到0000
便是四个二进制位都需要变化
现有的方法似乎有问题了
更一般的来讲,格雷码的特性似乎只能满足2^n种状态,如果实际需要不是呢?
通过观察上面的表格可以发现,格雷码具有对称性。0-15这16个格雷码,如果前后去掉相同个数的格雷码,那么剩余的格雷码仍然符合相邻两个数只有1 bit的跳变,也包括最后一个到第一个的跳变。

如果只需要10个状态,可以同时去掉开头三个和结尾三个。
- 我们在由addr得到格雷码时不能直接转换,而是要使用addr + 3进行转换;同理由格雷码转换回addr时,也不要忘记减去3。
- 使用这种编码时,FIFO的满判断逻辑就不是简单的高两位相反,低位相同了。
Reference
格雷码Gray Code详解
FIFO设计中与深度depth相关的问题 作者的文章质量很高,指的学习
异步FIFO设计 一个完整的异步FIFO设计(虽然本文没有引用)

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








