【C语言】B 树全代码实现与超超详细思路解读（五天的呕心沥血，绝对原创每个细节，详解查找、插入与删除）

---

—— 前言 ——

期末到了，数据结构老师安排了最后的实验作业
本着深入理解 B 树，本澈一步一步按照理论思路撸了一遍代码
过程非常曲折，各种 bug 层出不穷，debug 算是安排的明明白白
其中参照了不少其他人的代码，最终手撕了这份 B 树代码，已经最大程度地保证了无 bug 出现

整篇博客写完之后，我认为这是我目前写的最投入感情的一次了
嘛虽然可能大家看不出来，但在这几天的自己一点点摸索，而不是通过学校老师或者 B 站网课老师直接输入知识，到最后往回看还是蛮感动的，也祝屏幕前的你好运~

▲ 在这里还是需要特别声明一下 本人来自 广东工业大学 （） 如果你也是广工一员而且需要完成本次实验作业，要注意不能直接拷贝代码哦（思路也是噢，本人会写进实验报告的） 本人代码思路与网上和课本上的都有明显的区别，被辨识出来雷同就不好了（重点在于了解实现思路与代码思路以及避雷） 不过，在本篇博客中，除了代码上有非常详细的注释，我还将自己在实现 B 树过程中的很多思路、想法以及踩到的坑记录在里边 相信聪明的你读完整篇博客后，自己手撕一份 B 树代码肯定是没问题的~ （想自己手撕的，可以只看代码前的思路解读以及代码段中间的黄色框框注意点，直接看代码容易限制思路） 当然，如果是单纯想学习的，那么请随意~ 希望本篇分享能帮到正努力向前的你，oo，o！

● 彩蛋预告： 在调整树形那一部分，有一份 B 树本身留给大家的礼物，这是我在写博客期间惊喜发现的 希望大家都能坚持用心看到那里，相信在收到这份礼物后，你可能会对数据结构有新的想法哦

B 树全代码实现与思路解读

接下来就正式进入主题啦（嘛，可能前面废话有点多）

① 结构体与宏定义

需要提前定义以下常量，方便后续的使用

/* B 树阶数 */
#define M 4

/* B 树关键最大最小值以及中间值 */
#define MAX_KEY (M-1)
#define MIN_KEY ((M-1)/2)
#define MID_KEY ((M+1)/2)

注意点1： 对于三个 KEY 值的解释 MAX_KEY 应该很好理解，M 接 B 树就是该树最多有 M 棵子树，那 M-1 个关键字自然就会留出 M 个子树的位置啦 MIN_KEY 的话，按照定义应该是 M/2 向上取整为子树数量，但是整型除法默认是向下取整呀，所以我们需要调整成 (M+1)/2，这样相当于被 2 除的向上取整了，然后对应的关键字数量自然就是 (M+1)/2 - 1 即 (M-1)/2 啦 MID_KEY 作为分裂时需要移动到上层的记录的位置，注意这个值和前面的最大最小值有明显的区别哦，前边的表示数量，而该值表示的是“位置”。右应为 KEY 的第一个位置不存值，位置应该从 1 开始数，所以本来中间位置应该是 M/2 的，在第一个位置不使用之后，自然就变成了 (M+1)/2 啦

然后准备以下 3 个结构体

/* 记录类型 */
typedef struct Rcd {
	int key;		// 记录的键
	int data;		// 记录的值
} Rcd, *Record;

/* B 树结构体 */
typedef struct BTNode {
	int keyNum;					// 结点中关键字个数，即结点的大小
	KeyType key[M + 1];			// 关键字数组，0 号单元未用
	Record rcd[M + 1];			// 记录指针数组，0 号单元未用
	struct BTNode* parent;		// 指向双亲结点
	struct BTNode* child[M + 1];// 子树指针数组，0 号有使用
} BTNode, *BTree;

/* 结果类型 */
typedef struct Result {
	int i;		// 在结点中的关键字位序
	int tag;	// 是否找到了
	BTree data;	// 找到的数据
} Result;

然后是所有的接口

/* 通用辅助接口 */
Record getRecord(int key, int data);			// 获得一个记录值
Result getResult(int i, int tag, BTree data);	// 获得一个结果值

/* B 树接口 */
Status InitBTree(BTree& tree, Record data);		// 初始化 B 树
BTree MakeBTree(const int treeData[][2], int num);		// 构建 B 树 
void TraverseBTree(BTree tree);					// 打印 B 树
Result SearchBTree(BTree tree, KeyType key);	// 对 B 树执行查找操作
Status InsertBTree(BTree& tree, Record data);	// 对 B 树执行插入操作
Status DeleteBTree(BTree tree, KeyType key);	// 对 B 树执行删除操作
Status UpdateBTree(BTree tree, KeyType key, Record data);	// 将 B 树中关键字为 key 的结点记录更换成新的记录

/* B 树辅助接口 */
int Search(BTree node, KeyType key);	// 寻找 key 在 node 所在结点中的位置
void InsertBTNode(BTree& node, int i, Record rcd, BTree newNode);	// 将新记录 rcd 插入到结点 node 的第 i 个位置，同时将新子节点 newNode 作为后继孩子
Status SplitBTNode(BTree& node, BTree& newNode);	// 将 node 结点从中间分裂成两部分，前半部分留在原位，后半部分进入 newNode 并指向原结点的双亲
Status newRoot(BTree& root, Record rcd, BTree child1, BTree child2);	// 生成一个新根
int CountKeyNum(BTree tree);	// 计算出整棵树上记录条数的总和
void Successor(BTree& node, int& i);	// 找到前驱结点，并进行关键字的替换
Status InsertRecord(BTree& node, int i, Record rcd);	// 将 rcd 插入到指定结点的第 i 个位置
Status RemoveRecord(BTree& node, int i);	// 将指定结点中第 i 个记录移除
void RestoreBTree(BTree& node, int pi);		// 针对某个结点调整一颗 B 树
void CombineBTNode(BTree& left, BTree& right);	// 将右结点合并到左结点，结果放在左结点 left 中，右结点 right 将被释放
void DeleteRoot(BTree& root);	// 删除一个空根
void PrintBTree(BTree tree, int isLast[], int nowNum);	// 递归打印树形
void printBranch(int isLast[], int nowNum);	// 打印树枝

② 查询操作

对于 B 树的查询，是往后插入和删除的根基，重点在于理解与用好结果集 Result

Result 的三个值，tag 表示是否查询得到，data 表示找到的整一个 B 树结点
而重点在于 i 值，该值有两种情况，且无论找没找着，它都非常有用
① 如果找到了，i 值就是当前记录值所在位置（从 1 开始算）
② 如果没找到，i 值就是所查询的结点本应该在的位置，该位置是孩子 child 的位置（从 0 开始算），对于后面的插入和删除都有很重要的作用

与之对应一个很重要的函数就是 Search 函数（如下），它实现了 Result 中 i 值的逻辑

/* 寻找 key 在 node 所在结点中的位置 */
int Search(BTree node, KeyType key) {
	// 判空
	if (node == NULL) return 1;

	int i = 1;
	while (i <= node->keyNum && key > node->key[i]) i++;
	return i;
}

这里需要好好理解 i 的含义，i 从 1开始，遍历所有关键字，直到碰到不比提供的 key 小的关键字，便停下
此时有可能是相等（找到了），也可能是小于（没找到，此时 i 正是 key 原本该在的位置），返回该值，查询代码如下：

/* 对 B 树执行查找操作 */
Result SearchBTree(BTree tree, KeyType key) {
	// 当前正在遍历的结点（指向传进来的树），以及其双亲结点（用于结果返回）
	BTree now = tree, parent = NULL;

	int i = 0, found = 0;
	while (now != NULL && found == 0) {
		// 找到 key 在当前结点的位置
		i = Search(now, key);

		// 判断该位置是否为所需的值
		if (i <= now->keyNum && key == now->key[i]) found = 1;
		// 没找到的话，继续往下找
		else {
			parent = now;
			now = now->child[i - 1];
		}
	}

	// 找到的话，返回目标结点以及数据所在结点的位置
	if (found == 1) return getResult(i, 1, now);
	// 如果没找到，返回该数据所应该插入的结点及其所在结点的位置
	return getResult(i, 0, parent);
}

/* 获得一个结果类型 */
Result getResult(int i, int tag, BTree data) {
	Result result;
	result.i = i;
	result.tag = tag;
	result.data = data;

	return result;
}

查询实现不难，就是不断找到 key 应该在的地方，对比该地方是否为所需要的值
如果不是，则保留当前值作为双亲存起来（为什么要呢？），再继续向下寻找

注意点2： 这里可以注意到，now = now->child[i - 1] 中的 i-1，为什么是 i-1 呢？ 因为 i 值表示的是 key 所该在的位置，但目前的位置不是 key，而是比 key 大的值，所以要找 key 应该找该记录的左孩子（找小的），即找 i-1

这里有一个技巧，如果 i 值是指向某记录，则 child[i-1] 为该记录的左孩子，child[i] 为该记录的右孩子
接着如果正常找到了，则返回 getResult(i, 1, now) 即 key 所在结点 now 和其在结点的位置 i

注意点3： 但如果没找到呢？返回的是 getResult(i, 0, parent)，这里就是 parent 和 i 的作用所在了 没找到的话，i 就表示 key 本来应该存放在 parent 中的位置，为插入和删除操作做准备

③ 打印操作

在了解插入和删除操作之前，大家可以先搞一下树形的打印，为过程中验证结果作准备
B 树的打印函数参考了：https://blog.csdn.net/Baibair/article/details/112055649 这篇博客
本人只是将其修改成 C 语言以及稍微美化一下，感谢这位师兄（应该是师兄吧~）

打印的具体逻辑就不废话了，直接上代码

/* 计算出整棵树上记录条数的总和 */
int CountKeyNum(BTree tree) {
	// 空树则为 0
	if (tree == NULL) return 0;

	// 计算所有子树记录条数总和
	int childTotal = 0;
	for (int i = 0; i <= tree->keyNum; i++) {
		childTotal += CountKeyNum(tree->child[i]);
	}

	// 子树加上自身的记录条数，即为总记录条数
	return tree->keyNum + childTotal;
}

/* 打印 B 树 */
void TraverseBTree(BTree tree) {
	// 动态创建一个数组，用于存放当前结点是否为最后结点的标识
	int nowNum = 0;
	int* isLast = (int*)malloc(sizeof(int) * (CountKeyNum(tree) + 10));
	
	// 打印树形
	printf("\n");
	PrintBTree(tree, isLast, nowNum);
}

/* 递归打印树形 */
void PrintBTree(BTree tree, int isLast[], int nowNum) {
	// 空树直接跳过
	if (tree == NULL) return;

	// 打印新节点先打印一下平台
	printf("┓\n");
	for (int i = 0; i <= tree->keyNum; i++) {
		if (tree->child[i] != NULL) {
			printBranch(isLast, nowNum);
			printf("┣━━━━━━");
			isLast[nowNum++] = (i == tree->keyNum);
			PrintBTree(tree->child[i], isLast, nowNum);
			nowNum--;
		}
		if (i != tree->keyNum) {
			printBranch(isLast, nowNum);
			printf("┣━ %d\n", tree->key[i+1]);
		}
	}
}

/* 打印树枝 */
void printBranch(int isLast[], int nowNum) {
	for (int i = 0; i < nowNum; i++) {
		if (isLast[i]) printf(" ");
		else printf("┃");
		printf("      ");
	}
}

下面是打印完的树形，还是非常清新的

④ 插入操作

接着是插入操作，该操作比查询要复杂许多
即便在理论层面上完全理解了该操作是什么样子的，但实现起来还是屡屡碰壁，插入思路如下：

• 先通过查找操作获得结果集 Result，利用找到的结点 data 和 位置 i，直接将记录插入到对应位置中
  由于插入操作必然发生在叶子节点中，故插入后该记录的右孩子为 NULL
• 然后判断是否超过关键字数量最大值，如果是的话则分裂
  分裂出来的左半部分存放在原结点，右半部分存放在新结点，中间部分单独作插入处理
• 如果需要分裂的是根节点，则中间部分作为新根，左右孩子分别指向分裂好的左右半部分
  如果非根节点，则将中间部分插入到双亲结点中
• 最后将结点移动到双亲结点，检查双亲是否也需要分裂，循环分裂

原理之后，实现代码如下：

/* 对 B 树执行插入操作 */
Status InsertBTree(BTree& tree, Record rcd) {
	// 树为空时，新建根节点
	if (tree == NULL) return InitBTree(tree, rcd);
	
	// 树非空时，先进行查找
	Result result = SearchBTree(tree, rcd->key);

	// 若记录存在，则插入失败
	if (result.tag == 1) return ERROR;
	// 记录不存在，则在找到的结点中插入新记录，该新记录的后继孩子为空
	InsertBTNode(result.data, result.i, rcd, NULL);

	// 判断本结点存放的关键字是否越界了，越界则进行分裂操作
	BTree newNode;
	while (result.data->keyNum > MAX_KEY) {
		// 分裂本结点，使其右半部分到 newNode 中
		SplitBTNode(result.data, newNode);

		// 如果结点为根节点，则直接生成新根
		if (result.data->parent == NULL) newRoot(tree, result.data->rcd[MID_KEY], result.data, newNode);
		// 否则将中间记录插入到双亲结点中，然后将 result.data 作为左孩子， newNode 作为右孩子
		else {
			// 找到中间记录需要插入到双亲的哪个位置
			int pi = Search(result.data->parent, result.data->key[MID_KEY]);
			// 将记录插入到双亲的 pi 位置，并将 newNode 作为右孩子
			InsertBTNode(result.data->parent, pi, result.data->rcd[MID_KEY], newNode);
		}
		
		// 将结果结点移动到其双亲，继续检测双亲是否需要分裂
		result.data = result.data->parent;
	}
	return OK;
}

注意点4： 整体逻辑这里需要注意的是分裂后对左右两个结点的处理，因为分裂可能发生在根和非终端结点中 如果是在根结点则需要新建一个初始值为中间值的根（中间值放到双亲位置上了），然后左右孩子分别是分裂出来的两部分 如果是在非终端节点，那首先需要得到中间值应该插入到双亲的位置，这里通过 Search 函数找到该位置（注意这里 i 代表关键字位置），然后分裂出来的右结点作为该位置的右孩子

插入函数实现了整体的逻辑，但重点还是在于各个辅助函数：InsertBTNode SplitBTNode 和 newRoot

/* 将新记录 rcd 插入到结点 node 的第 i 个位置，同时将新子节点 newNode 作为后继孩子 */
void InsertBTNode(BTree& node, int i, Record rcd, BTree newNode) {
	// 从最后面开始，依次将记录往后移动
	for (int j = node->keyNum; j >= i; j--) {
		node->key[j + 1] = node->key[j];
		node->rcd[j + 1] = node->rcd[j];
		node->child[j + 1] = node->child[j];
	}

	// 空出一个位置给新记录
	node->keyNum++;
	node->key[i] = rcd->key;
	node->rcd[i] = rcd;
	node->child[i] = newNode;

	// 如果新结点不为空，则将其双亲置为本结点
	if (newNode != NULL) newNode->parent = node;
}

InsertBTNode 函数实现了将记录和对应孩子插入到指定结点位置的功能，是个基本操作，后边很多地方会用到

/* 将 node 结点从中间分裂成两部分，前半部分留在原位，后半部分进入 newNode 并指向原结点的双亲 */
Status SplitBTNode(BTree& node, BTree& newNode) {
	// 生成新结点，并使其指向原结点 node 的双亲，作为兄弟存在
	newNode = (BTree)malloc(sizeof(BTNode));
	if (newNode == NULL) return OVERFLOW;

	newNode->keyNum = 0;
	newNode->parent = node->parent;

	// 中间值的右孩子应该作为新结点的左孩子
	newNode->child[0] = node->child[MID_KEY];
	// 同理中间值的右孩子双亲应指向新结点（这个非常非常重要，掉坑了。不修改的话，后边孩子的双亲关系会乱套，致命！）
	if (node->child[MID_KEY] != NULL) node->child[MID_KEY]->parent = newNode;
	// 将其余的孩子置空
	for (int i = 1; i <= M; i++) newNode->child[i] = NULL;

	// 中间值后面的数据全部搬到新结点
	for (int i = MID_KEY + 1, j = 1; i <= M; i++, j++) {
		InsertBTNode(newNode, j, node->rcd[i], node->child[i]);
		node->rcd[i] = NULL;
	}
	
	// 更新原结点的 keyNum
	node->keyNum = MID_KEY - 1;

	return OK;
}

注意点5： 分裂函数是插入操作最重要的一步，其中最重要的是对孩子归属的处理 新产生的新结点，双亲应该和受分裂的节点一样，而左孩子应该是中间值的右孩子（需双向设置双亲的孩子指针和孩子的双亲指针），而受分裂节点本身并不需要变化，孩子指针和双亲均没发生变化 可以说，分裂操作完成了新结点的双亲指定以及其与孩子的双向绑定，但双亲并没有将新结点作为孩子（这一点需要明确） 所以接下来的操作 newRoot 和 InsertBTNode 就是完成双亲和新结点的

完整的分裂过程可以看下面一张图帮助理解（4 阶 B 树）

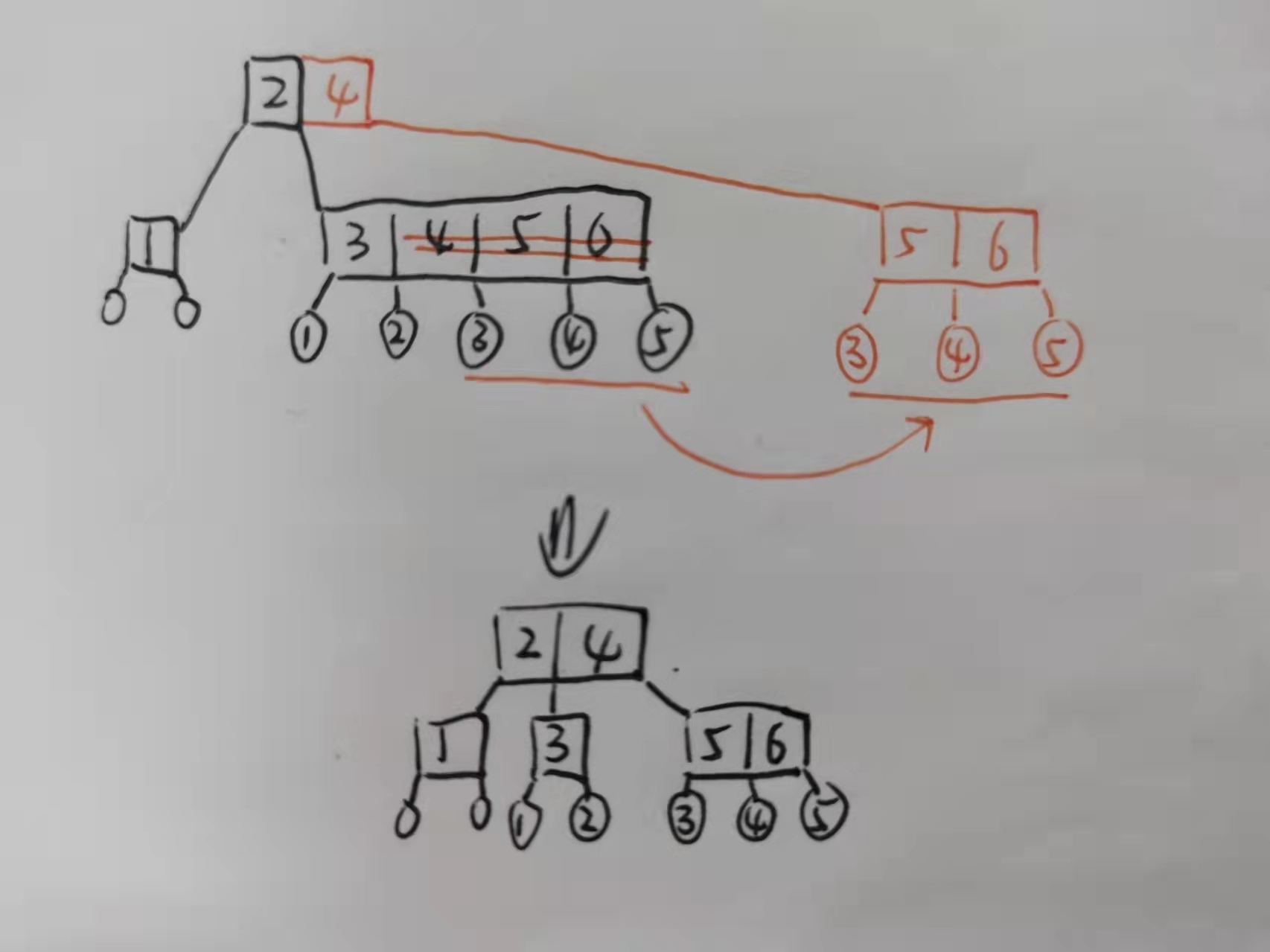
可以看到，生成新节点后， 中间记录 4 的右孩子 ③ 需要作为新结点的左孩子，而记录 3 则不需要改变，依旧拥有左右俩个孩子以及正确指向了双亲。新结点的 5 6 记录及其右孩子，则由函数 InsertBTNode 完成

/* 生成一个新根 */
Status newRoot(BTree& root, Record rcd, BTree child1, BTree child2) {
	// 初始化根
	if (!InitBTree(root, rcd)) return ERROR;

	// 然后将根可能存在的俩个孩子赋值给根
	root->child[0] = child1;
	root->child[1] = child2;

	// 再将两个可能存在的孩子的双亲设置为该根
	if (child1 != NULL) child1->parent = root;
	if (child2 != NULL) child2->parent = root;

	return OK;
}

生成新根就比较好写了，就是将记录初始化为新树，然后将左右两部分分别作为左右孩子
因为有前边的分裂作为铺垫，新结点已经和孩子进行双向绑定，接下来就剩双亲来认领新结点了（图例如下）

至此插入操作已经完成了，集中最需要注意的地方是：每一次分配新结点，生成新根，都需要调整好双亲和孩子的关系，一定要保证双亲和孩子是双向绑定的（不能双亲认了孩子，孩子不认双亲，这种关系缺陷很隐蔽，反过来的话在打印阶段就能发现了）

⑤ 删除操作

最后就是重头戏了，删除操作，最难的地方就在于删除后对树形的调整
在调整的过程中，依旧要牢记一个问题：双亲和孩子的双向绑定（这是在踩了很多坑后总结出来的）

删除操作思路如下：

• 首先依旧通过查询操作获得结果集 Result，找不到的话（tag=0）直接返回
  通过找到的结点判断其是否为最底层非终端结点，如果不是的话，则通过 Successor 函数找到要删除的 key 的前驱关键字，替换原关键字，转化为删除最底层非终端节点
• 在删除最底层非终端结点时，我采取的方法是先记下该结点在双亲中的位置，好在后续需要向兄弟或者双亲借记录时，能快速找到它们。这里我的思路是先将要删除的 key 保留下来，然后再删除该 key，最后重新到该结点的双亲寻找该 key，可以预知，该 key 已经不存了不可能找到，所以能找到的只有其本应该在双亲中的位置，通过该位置就能快速定位到左右双亲以及左右兄弟
• 删除完毕后，再进行树形的调整（重中之重）

首先先上整体逻辑代码

/* 对 B 树执行删除操作 */
Status DeleteBTree(BTree tree, KeyType key) {
	// 先找到需要删除的结点，不存在该节点则返回失败
	Result result = SearchBTree(tree, key);
	if (result.tag == 0) return UNSUCCESS;

	// 找到该结点后，若非最下层非终端结点，则处理成最下层非终端结点
	// 将前驱记录替换要删除的记录，并且 data 和 i 换成前驱结点及其记录的位置，即转化为删除最下层非终端结点
	if (result.data->child[0] != NULL) Successor(result.data, result.i);
	
	// 先将要删除的 key 保留下来
	key = result.data->key[result.i];
	// 再将指定的记录删除
	RemoveRecord(result.data, result.i);
	// 然后就可以通过保留的 key 找到要删除的记录在双亲结点的位置
	// 因为 key 已经被删除，所以可以定位到其本应该再双亲结点的位置，为下面调整树形做准备
	int pi = Search(result.data->parent, key) - 1;

	// 判断删除之后，若关键字数量小于最小数量，需另外处理
	// 如果是根，则不需要调整了，因为既然删除操作发生在了根，说明已经没有左右兄弟和双亲了
	if (result.data->parent != NULL && result.data->keyNum < MIN_KEY) RestoreBTree(result.data, pi);

	return OK;
}

注意点6： 这里的 RestoreBTree 函数，我和其他地方的不一样，参数 pi 并不是关键字在目标结点中的位置，而是整个目标节点在双亲节点中的位置，这样做的好处上边也提到了，可以很方便地找到左右双亲和左右兄弟 也可以注意到 pi = Search -1; 这一句，和上边的 child[i-1] 是一样的道理，都是找到双亲中孩子的位置

然后一步一步来，Successor 函数其实是做了两件事（在我的代码思路中是这样）
第一件是找到前驱关键字后，将其替换调原结点的记录值
第二件是将需要删除的结点及其位置换成前驱节点及其关键字的位置，为接下来继续删除提供条件

/*
* 找到非最底层非终端节点节点的前驱节点
* 并将结点 node 换成前驱结点
* 将位置 i 换成前驱节点需要删除的关键字的位置
*/
void Successor(BTree& node, int& i) {
	// 判非法输入（结点为空或为最底层非终端结g点）
	if (node == NULL) return;
	if (node->child[i - 1] == NULL) return;

	// 找到左子树最右边的值
	BTree search = node->child[i - 1];
	while (search->child[search->keyNum] != NULL) search = search->child[search->keyNum];

	// 替换掉原结点的的记录值
	node->key[i] = search->key[search->keyNum];
	node->rcd[i] = search->rcd[search->keyNum];

	// 最后修改结点和位置信息为前驱结点的信息
	node = search;
	i = search->keyNum;
}

调整完毕之后，就是正式删除最底层非终端结点了
按找思路先保存该结点在双亲中的位置，然后删除记录（代码如下）

/* 将指定结点中第 i 个记录移除 */
Status RemoveRecord(BTree& node, int i) {
	// 判空
	if (node == NULL) return UNSUCCESS;

	// 将所有记录前移
	for (; i < node->keyNum; i++) {
		node->key[i] = node->key[i + 1];
		node->rcd[i] = node->rcd[i + 1];
	}

	node->keyNum--;
	node->rcd[i] = NULL;

	return SUCCESS;
}

/* 将 rcd 插入到指定结点的第 i 个位置 */
Status InsertRecord(BTree& node, int i, Record rcd) {
	// 判空
	if (node == NULL) return UNSUCCESS;

	// 从最后面开始，依次将记录往后移动
	for (int j = node->keyNum; j >= i; j--) {
		node->key[j + 1] = node->key[j];
		node->rcd[j + 1] = node->rcd[j];
	}

	// 空出一个位置给新记录
	node->key[i] = rcd->key;
	node->rcd[i] = rcd;
	node->keyNum++;
}

注意点7： 删除记录这一部分，我省略了删除孩子指针的步骤，为什么呢？ 这里是为了方便后续的树形调整函数 如果只删除记录的话，会导致孩子指针比原本多出一个，但好处也很明显，到后边有一个双亲记录替换的需求，我提供了只删除记录和只插入记录的操作，可以在不影响孩子指针的情况下完成记录值的替换

这个操作也不难理解，下面就是全文重点了，调整树形（代码如下）
里边所有的操作我都是基于基本操作和理论思路来的，按照下面思路走一遍应该就很清晰了

删除操作后树形需要调整的情况，无非就是某一结点的关键字数目小于最小的关键字数目了，需要向亲戚借
而借的对象有 4 个，左右兄弟和左右双亲，所以对应的可以分为 4 种情况：

• ① 左兄弟有富余记录： 这时可以将左兄弟的记录值补到目标节点中
  • 但不能够直接交换值，因为左兄弟最大的值，也比左双亲的值小
    而目标节点作为左双亲的右孩子，值肯定都是需要比左双亲大的
  • 这时候，就只能先将左双亲的记录拿下来，然后将左兄弟的记录补回左双亲，完成一次交换
    且左双亲取下的记录为受调结点记录的最小值，应插入到第 1 个位置，而左兄弟需要拿最大记录补回去
    注意这时候双亲结点的孩子并没发生变化，双亲与孩子的双向绑定没影响到，只是完成了记录值的交换
  • 但对于左兄弟和目标节点来说，与孩子的双向绑定关系是需要改变的
    目标结点由于插入了一条来自双亲的记录，原本的左孩子需成为新记录的右孩子（原左孩子比双亲记录大）
    而新记录的左孩子空出来了，需要由左兄弟最大记录值的右孩子来填充（刚好该记录值补回双亲后，会多出最右边一个孩子，这个孩子比双亲记录值小，所以作为目标节点新记录值的左孩子刚刚好）
  • 以上操作相当于完成了一次右旋
• ② 右兄弟有富余记录： 该情况和上边一种是对称关系，即需要完成一次左旋，但处理上略有不同
  • 首先依旧是不能直接交换值，而是将右双亲记录拿下来，右兄弟记录补上去
    右双亲的记录应插入到受调结点的最后一个位置，而右兄弟需要取第 1 个记录补回去
  • 然后对于孩子的绑定关系，右双亲记录插入到目标节点的最右边，空出来一个右孩子，由右兄弟第 0 个孩子作为补充
• ③ 左右兄弟穷，先向左右双亲取（算 2 种情况）： 这种情况不管双亲够不够借，都可以直接拿下来（来自爹妈的爱）
  • 这里向双亲取值和上边的过程差不多，依旧是将双亲的记录拿下来，再删除双亲的记录值
  • 但需要注意的是，已经没有来自左右孩子的记录补充了，所以双亲的孩子数量会减少 1
    此时就需要将受调兄弟与左右兄弟合并起来（向左双亲借则和左兄弟合并，向右双亲则和右兄弟）
    然后双亲的孩子指针也需要手动左移（上边也提到了，对记录的操作被设计为不影响孩子指针，此时就需要手动了）
  • 最后借完之后，还需要看看双亲是否也需要调整树形（孩子需要先拿去，自己不够再向亲戚借，类目了）
    但这也需要分情况，双亲已经是根结点以及不是根节点
    • 是根节点的话，说明双亲以及没有兄弟，也没有双亲了，也就意味着她，哪里都借不了
      而由 B 树定义我们知道，根节点最少有两棵子树，也就是最少 1 个关键字，这时候如果关键字数不够且是根节点的话，只有一种情况，那就是双亲已经没有关键字了，空空如也。而孩子合并之后，也只可能是该根节点的唯一孩子。所以这时候，老根就只能在最后的力气给予孩子之后沉眠，永远退出这棵 B 树，而唯一的孩子代替她成为新根（哇，没想到一个数据结构，也能产生这么一段感人的故事，这时我在写代码时没有注意到的，再次类目）
    • 如果双亲不是新根的话，那么好办，继续递归调整双亲的树形

注意点8： 上边提到的向双亲借的情况，需要俩兄弟合并，那这样做会不会使合并后的关键字数量超出范围呢？ 答案是不会的，不用担心 因为按照定义，最小关键字数量是 (M-1)/2，而需要借的情况，在向双亲借了一个之后也是该值 (M-1)/2 而即便与之合并的兄弟节点关键字则是刚好达到最小关键字数（否则就去向兄弟借啦），也就是 (M-1)/2 那么两个值加起来，即两个关键字最小数相加，最多也只能是 M-1，刚好等于关键字最大数，并不会超出

/*
* 针对某个结点调整一颗 B 树
* node	：受调整的结点
* pi	：受调整结点在双亲结点的位置
*/
void RestoreBTree(BTree& node, int pi) {
	// 双亲和可能存在的左右兄弟
	BTree parent, brother;
	parent = node->parent;

	// 用于递归调整双亲的记录存储
	KeyType key;

	// 先看看左兄弟有没有可以借的
	if (pi > 0 && (brother = parent->child[pi - 1])->keyNum > MIN_KEY) {
		// 先将左双亲的记录拿下来（从左双亲拿的记录，必为受调整结点记录的最小值，直接插入到受调结点的第 1 位，插入后新记录的右孩子为原先的第 0 位孩子）
		// 这里是将第 0 位孩子插入到第 1 位，相当于第 0 和 1 俩个孩子是一样的，只不过为了将 0 好位置腾出来接纳左兄弟最大的孩子，和向右兄弟借的情况不太一样
		InsertBTNode(node, 1, parent->rcd[pi], node->child[0]);
		// 然后修改新记录的左孩子，应为左兄弟的最大的孩子
		node->child[0] = brother->child[brother->keyNum];
		if (brother->child[brother->keyNum] != NULL) brother->child[brother->keyNum]->parent = node;
		// 然后将左双亲记录删去（这里仅仅只是删除记录，而不动孩子指针，因为删除了该记录，还有来自左兄弟的记录补给呀）
		RemoveRecord(parent, pi);
		// 再将左兄弟的值补回左双亲（从左孩子拿的记录，必为左兄弟最大的一位，且插入到双亲的第 pi 位，做双亲右孩子不改变，插在第 pi 位右孩子位置为 pi）
		InsertRecord(parent, pi, brother->rcd[brother->keyNum]);
		// 最后将左兄弟对应记录删去
		RemoveRecord(brother, brother->keyNum);
	}
	// 再看看右兄弟，其操作思路同理左兄弟，只不过细节略微不同
	else if (pi < parent->keyNum && (brother = parent->child[pi + 1])->keyNum > MIN_KEY) {
		// 首先将右双亲的记录拿下来插入到最右边（比受调结点所有记录都大），且新记录的右孩子为右兄弟最小的孩子（该最小孩子是受调结点的最大孩子）
		// 这里直接将右兄弟最小孩子插入即可，不需要再挪动孩子位置了
		InsertBTNode(node, node->keyNum + 1, parent->rcd[pi + 1], brother->child[0]);
		// 然后继续删除右双亲记录，插入右兄弟记录，再删除右兄弟记录
		RemoveRecord(parent, pi + 1);
		InsertRecord(parent, pi + 1, brother->rcd[1]);
		RemoveRecord(brother, 1);
		// 最后多了一步，将左兄弟最小孩子的指针删去（这里将右兄弟第 1 条记录删除了，最左边的记录已经被拿走了，此时因为是在第一位对后边有影响，故需要删掉，不同于上边）
		for (int i=0; i <= brother->keyNum; i++) brother->child[i] = brother->child[i + 1];
	}
	// 都没有的话直接向双亲借，这里先向左双亲借
	else if (pi > 0) {
		brother = parent->child[pi - 1];
		// 先将左双亲的记录拿下来，同样将受调结点的最小孩子向右挪动一位
		InsertBTNode(node, 1, parent->rcd[pi], node->child[0]);
		// 然后将左双亲记录删去
		RemoveRecord(parent, pi);
		// 再将受调结点合并到左兄弟，并释放掉受调结点（这时候原本受调结点空出来的最小孩子，刚好由左兄弟的最大孩子填补了）
		CombineBTNode(brother, node);
		// 这时记得把 node 补回来，因为函数的设计默认是合并到左兄弟，而右兄弟被释放
		node = brother;
		// 最后将左双亲 pi 处的孩子指针也删去（因为左双亲的记录被拿走了，而且没有新记录补充）
		for (int i = pi; i <= parent->keyNum; i++) parent->child[i] = parent->child[i + 1];

		// 借完之后再看看双亲需不需要调整
		if (parent->keyNum < MIN_KEY) {
			// 如果需要调整的是根结点的话，此时的根节点必然没有关键字了（因为根节点最少的关键字数是 1）
			// 此时根节点必然只有一个孩子，所以直接将该孩子代替根节点，就解决了
			if (parent->parent == NULL) DeleteRoot(parent);
			// 否则的话继续调整双亲结点
			else RestoreBTree(parent, Search(parent->parent, node->key[1]) - 1);
		}
	}
	// 没有左双亲的话（受调结点在最左边了），则向右双亲借，操作思路同理，这里就不写注释了
	else {
		brother = parent->child[pi + 1];
		InsertBTNode(node, node->keyNum + 1, parent->rcd[pi + 1], brother->child[0]);
		RemoveRecord(parent, pi + 1);
		CombineBTNode(node, brother);
		// 最后将左双亲 pi 处的孩子指针也删去（因为左双亲的记录被拿走了，而且没有新记录补充）
		for (int i = pi + 1; i <= parent->keyNum; i++) parent->child[i] = parent->child[i + 1];

		if (parent->keyNum < MIN_KEY) {
			if (parent->parent == NULL) DeleteRoot(parent);
			else RestoreBTree(parent, Search(parent->parent, node->key[node->keyNum + 1]) - 1);
		}
	}
}

注意点9： 我们注意到，上边的左右兄弟使用的是 child[pi-1] 和 child[pi+1] 这代表的是相对于当前结点 child[pi] 来说的左右兄弟，当然就是 pi-1 和 pi+1 了 需要和上边的 child[pi-1] 和 child[pi] 表示左右孩子区分开来，这种情况是相对于记录来说的 （小声）本人其中一个坑就是把这俩搞混了

/* 将右结点合并到左结点，结果放在左结点 left 中，右结点 right 将被释放 */
void CombineBTNode(BTree& left, BTree& right) {
	// 判异常操作
	if (left == NULL) return;

	// 将右节点的记录和孩子依次插入到左节点的最右边
	for (int i = 1; i <= right->keyNum; i++) {
		InsertBTNode(left, left->keyNum + 1, right->rcd[i], right->child[i]);
	}

	// 释放右结点
	free(right);
}

对于合并操作，需要做的就只是将右兄弟合并到左兄弟
为什么是这个顺序呢，因为左兄弟比右兄弟小，在合并时能直接将右兄弟插入到左兄弟后边，很方便
这里就隐含了一个逻辑，左兄弟最大的孩子指针变成了原右兄弟最小的孩子了，填补了右兄弟最小孩子空缺的情况
当然合并起来后就是一个结点了，很融洽的一个结点，其和双亲的双向绑定关系并没有改变

/* 删除一个空根 */
void DeleteRoot(BTree& root) {
	// 空根只有一个孩子
	BTree child = root->child[0];

	// 将该孩子的数据全都搬到新根，再释放孩子就行
	// 这里需要额外将第 0 个孩子指针移动到根结点（注意了，孩子的双亲需要手动改！）
	root->child[0] = child->child[0];
	if (child->child[0] != NULL) child->child[0]->parent = root;
	for (int i = 1; i <= child->keyNum; i++) InsertBTNode(root, i, child->rcd[i], child->child[i]);
}

最后删除空根这里，可以看到我都是直接选择 0 号单元，因为空根就只有一个孩子了（关键字数为 0）
然后和往常一样，在搬动结点时，注意手动将结点最小的孩子和双亲进行双向绑定
因为 InsertBTNode 是从第 1 个孩子开始绑定的

---

—— 结语 ——

最后，文章到这里就结束啦
能坚持看到这里结束还是很不容易的
希望大家看完能收获满满，这是对我最大的认可啦~（当然如果能给点鼓励的话，会更开心噢 /·v·\）

我自认为本文是很用心在写了
可能文中还有很多细节没有提到，如果大家有哪些地方还有些模糊的话
也非常欢迎大家提出来，我会将解析更新回文章中，让文章变得更有营养！

---

星之所在，心之所向（IceClean）