并查集优化——按秩归并、路径压缩

并查集优化——按秩归并、路径压缩

并查集的介绍（来自百度百科）

    并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。
    并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。

---

并查集（Union/Find）从名字可以看出，主要涉及两种基本操作:合并和查找。这说明，初始时并查集中的元素是不相交的，经过一系列的基本操作(Union)，最终合并成一个大的集合。而且我们可以从上面的描述中可以看到，并查集能够在一定程度上减小时间复杂度，让算法更加高效。首先定义一下我的并查集结构：

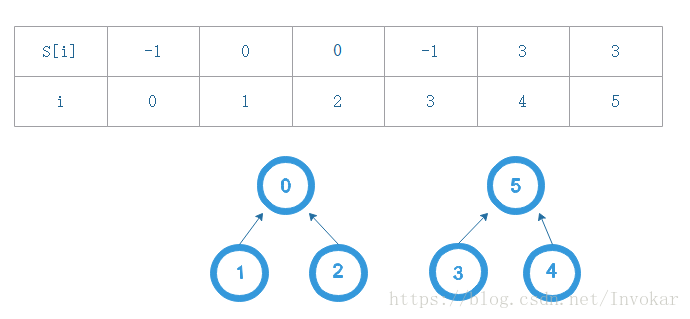
• S：存储儿子结点和父亲结点的数组，这里为了充分利用数组的下标，我们定义下标为儿子结点的编号，对应的S[i]表示该儿子结点所对应的父亲结点编号，并且规定根结点的父亲节点编号为-1。下面给一个示意图，方便大家理解。
  

接下来给大家展示两个普通Union和Find操作

void Union(SetType S, ElementType X1, ElementType X2)
{
    int Root1, Root2;   // 两个集合的根节点
    Root1 = Find(S, X1);
    Root2 = Find(S, X2);
    if (Root2 != Root1)
        S[Root2] = Root1;   // 如果两个根不相同说不两个集合不相交，于是把第二个集合指向第一个集合
}

int Find(SetType S, ElementType X1)
{
    for (; S[i] >= 0; i = S[i]);
    return i;
}

---

简单分析：
    从上面的代码中我们可以看出，这两种简单的方法都有一些弊端，对Union函数，对所有独立的集合合并，可能会出现下面这种情况：

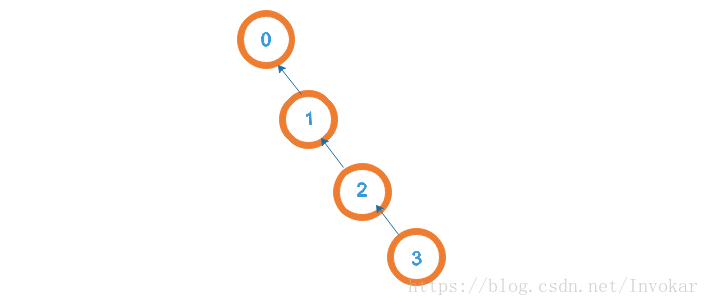
也就是这棵树会越长越高，如果在仔细看一下Find函数，如果每次都是找最底层的元素，那么这样的寻找代价就会是$O(N^2)$。因此我们有下面下面的改进方法（这里默认Root1和Root2是不同集合的根结点，默认集合元素全部初始化为-1）：

• 按树高归并：
  一点说明，这里秩大家可以简单地理解为树高，并且，一开始所有独立的结点树高我们都初始化为-1，此外，我们可以充分利用根结点的值-n，其中n为集合的高度。

void Union( SetType S, SetName Root1, SetName Root2 )
{
    if (S[Root2] < S[Root1])    // 注意到这里是负数，越小的越高
        S[Root1] = Root2;
    else
        if (S[Root2] == S[Root1])   // 如果树高相同
            S[Root2]--;     // 加深Root2的树高
        S[Root1] = Root2;   // 合并Root1到Root2
}

• 按规模归并
  一点说明，上面的n表示为集合的高度，这里的n我们表示数的儿子结点的个数。

void Union( SetType S, SetName Root1, SetName Root2 )
{ 
    if ( S[Root2] < S[Root1] ) 
    {   /* 如果S[Root2]规模比较大 */
        S[Root2] += S[Root1];    // 增加Root2的规模
        S[Root1] = Root2;        // 修改Root1的父节点
    }
    else 
    {                        
        S[Root1] += S[Root2];
        S[Root2] = Root1;
    }
}

注：以上两种统称为按秩归并，最坏情况下的树高为$O(\log_2N)$

---

说完了按秩归并，接下来就来说一下路径压缩。
这个操作主要做了以下3件事：

1. 先找到根
2. 把根变成X的父节点
3. 再返回根

接下来主要来说一下为什么要用路径压缩，先看一张图，我再解释。

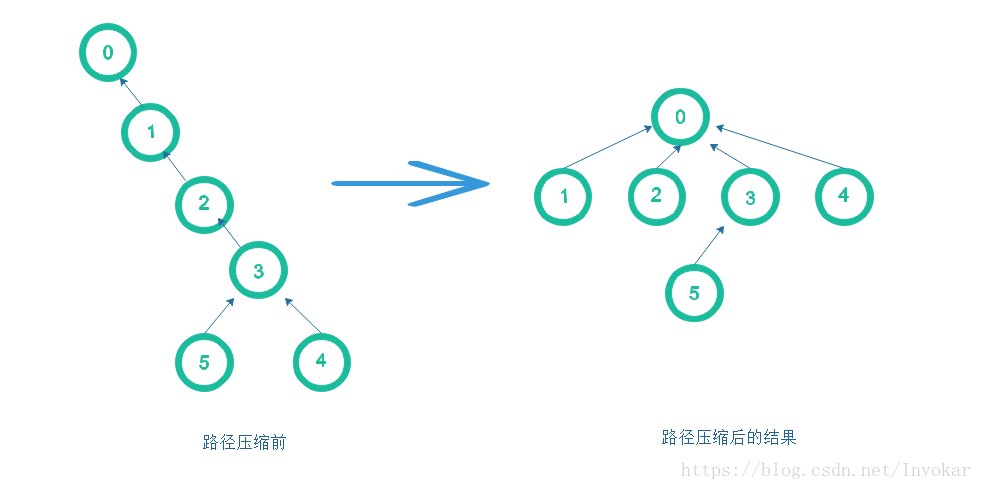
从图中我们可以看出，在用了路径压缩之后，整棵树会变矮，这给给我们带了一个好处，那就是如果我每次都要遍历最底下未寻找过的结点，对一棵不用按秩归并处理的树来说，需要$O(N^2)$的时间复杂度，对于用按秩归并的树来说，需要$O(Nlog_2N)$的时间复杂度。而如果我们做了路径压缩，很有可能在做Find操作时所需要的时间复杂度为$O(1)$。不过还需要声明的一点时，虽然路径压缩能带来查找上的遍历，但进行压缩的这一过程还是需要花费时间的。一般而言，我们对结点数大于$10^4$的情况来讲，用路径压缩提升的效果比较明显，对低于这个阈值的结点数的情况而言基本没有什么效果。这一原因我就不证明了，如果大家对这个证明过程比较感兴趣，可以去查阅Tarjan引理的相关资料。

路径压缩代码：

SetName Find( SetType S, ElementType X )
{ 
    if ( S[X] < 0 ) /* 找到集合的根 */
        return X;
    else
        return S[X] = Find( S, S[X] ); /* 路径压缩 */
}

如果大家不太清楚上面代码到底是如何实现路径压缩的过程，我在下面也会给出调试的代码，只需要运行一下，就能大致明白路径压缩的流程：
程序（里面的数组和上面的示意图所表示的内容一致）:

#include <iostream>
using namespace std;

int Find(int S[], int X)
{
    if (S[X] < 0)
        return X;
    else
    {
        cout << "Front:" << S[X]<< endl;
        S[X] = Find(S, S[X]);
        cout << "Rear:" << S[X] << endl;
        return S[X];
    }
}

int main(int argc, char const *argv[])
{
    int S[] = {-1, 0, 1, 2, 3,3};
    int root = Find(S, 4);
    for (int i = 0; i <= 5; i++)
        cout << "S[" << i << "] parent is " << S[i] << endl;
    return 0;
}

---

另外感谢陈越姥姥在MOOC上的讲解，令我受益很多~