（数论八）容斥原理与抽屉原理

一.先讲一下抽屉原理，其实高中的时候我们都学过，它可扩展为3个：

​ 1.把n + 1个物体放到n个抽屉，至少有一个抽屉里物件不少于2

​ 2.把mn + 1个物体放到n个抽屉，至少有一个抽屉里物件不少于m+1

​ 3.把无穷多个物体放到n个抽屉，至少有一个抽屉里有无穷多

它又衍生出来第二抽屉原理，即：

​ 把nm - 1个物体放到n个抽屉，必有一个抽屉中至多有m - 1个物体

定理就这么简单，但是想用好属实挺难～

​ 例如给你一个数组a和一个数m，问数组中能否选出几个数相加的和能被m整除？

​ 这个题咋一看和抽屉原理也没啥必然联系啊，那就再仔细瞅瞅。。

​ 联系抽屉原理，我们可以知道，当n > m时，必然能选出几个数的和被m整除。

​ 为什么？因为n个数求余m会产生n个余数，至少有两个相同的余数。

​ n个m以内的余数一定能组成m的倍数

​ 这样，我们只需要判断 n <= m时的情况即可

二. 容斥原理

​ 容斥原理原理是为避免重复计算的一种想法，很简单，同抽屉原理一样，难在活学活用～

​ 简单说一下容斥原理，例如下图，我们知道三个圆各自的面积，问三个圆一共占有的面积是多少？这时候为了避免重复运算，就需要用到容斥原理了：

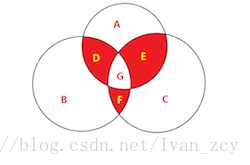
在此感谢百度百科提供的图片资源～～～

也就是说，3个圆占有的面积是三个圆的面积和 - 红色部分 + G部分

嗯嗯，原理就是这些，还是实战一下吧：

​ 1.例如从m种颜色挑选k种给n盆花染色，要求相邻花颜色不同，问方案数？

​ 从m种颜色挑选k种共有C(m, k)种方案数，而k种颜色给n盆花染色且相邻花颜色不同，这时候我们就可以利用容斥原理了。

​ 种类数应该是：可用k种颜色保证相邻花色不同的方案数 - 可用k - 1种颜色种颜色保证相邻花色不同的方案数+ 可用k - 1种颜色种颜色保证相邻花色不同的方案数…(-1)^(k - 1)✖️可用1种颜色种颜色保证相邻花色不同的方案数

​ 只需要把种类数✖️C(m, k)即为答案

​ 这样就可以简化思考的复杂度了～

​ 2.求区间(a, b)中与n互质的数的个数，例如求区间(a, b)中与12互质的个数

​ 我们可以先筛选出12的全部素因子2, 3，我们只需要求(a, b)的个数 - 素因子2对(a, b)的贡献 - 素因子3对(a, b)的贡献 + 因子(2✖️3)对(a, b)的贡献，即是最终答案。​

转载请注明出处！！！

如果有写的不对或者不全面的地方 可通过主页的联系方式进行指正，谢谢