高基数类别特征预处理：平均数编码 | 京东云技术团队

一 前言

对于一个类别特征，如果这个特征的取值非常多，则称它为高基数（high-cardinality）类别特征。在深度学习场景中，对于类别特征我们一般采用Embedding的方式，通过预训练或直接训练的方式将类别特征值编码成向量。在经典机器学习场景中，对于有序类别特征，我们可以使用LabelEncoder进行编码处理，对于低基数无序类别特征（在lightgbm中，默认取值个数小于等于4的类别特征），可以采用OneHotEncoder的方式进行编码，但是对于高基数无序类别特征，若直接采用OneHotEncoder的方式编码，在目前效果比较好的GBDT、Xgboost、lightgbm等树模型中，会出现特征稀疏性的问题，造成维度灾难， 若先对类别取值进行聚类分组，然后再进行OneHot编码，虽然可以降低特征的维度，但是聚类分组过程需要借助较强的业务经验知识。本文介绍一种针对高基数无序类别特征非常有效的预处理方法：平均数编码（Mean Encoding）。在很多数据挖掘类竞赛中，有许多人使用这种方法取得了非常优异的成绩。

二 原理

平均数编码，有些地方也称之为目标编码（Target Encoding），是一种基于目标变量统计（Target Statistics）的有监督编码方式。该方法基于贝叶斯思想，用先验概率和后验概率的加权平均值作为类别特征值的编码值，适用于分类和回归场景。平均数编码的公式如下所示：

其中：

1. prior为先验概率，在分类场景中表示样本属于某一个_y__i_的概率

​其中_n__y__i_​​表示y =_y__i_​时的样本数量，_n__y_​表示y的总数量；在回归场景下，先验概率为目标变量均值：

2. posterior为后验概率，在分类场景中表示类别特征为k时样本属于某一个_y__i_​的概率

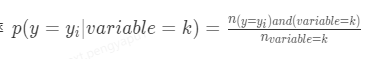
在回归场景下表示 类别特征为k时对应目标变量的均值。

3. _λ_为权重函数，本文中的权重函数公式相较于原论文做了变换，是一个单调递减函数，函数公式：

其中 输入是特征类别在训练集中出现的次数n，权重函数有两个参数：

① k：最小阈值，当n = k时，λ= 0.5，先验概率和后验概率的权重相同；当n < k时，λ> 0.5, 先验概率所占的权重更大。

② f：平滑因子，控制权重函数在拐点处的斜率，f越大，曲线坡度越缓。下面是k=1时，不同f对于权重函数的影响：

由图可知，f越大，权重函数S型曲线越缓，正则效应越强。

对于分类问题，在计算后验概率时，目标变量有C个类别，就有C个后验概率，且满足

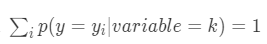
一个 _y__i_​ 的概率值必然和其他 _y__i_​ 的概率值线性相关，因此为了避免多重共线性问题，采用平均数编码后数据集将增加C-1列特征。对于回归问题，采用平均数编码后数据集将增加1列特征。

三 实践

平均数编码不仅可以对单个类别特征编码，也可以对具有层次结构的类别特征进行编码。比如地区特征，国家包含了省，省包含了市，市包含了街区，对于街区特征，每个街区特征对应的样本数量很少，以至于每个街区特征的编码值接近于先验概率。平均数编码通过加入不同层次的先验概率信息解决该问题。下面将以分类问题对这两个场景进行展开：

1. 单个类别特征编码：