统计学习方法笔记（理论+实例+课后习题+代码实现）：感知机

最新推荐文章于 2024-03-29 17:20:31 发布

Jackson_feng

最新推荐文章于 2024-03-29 17:20:31 发布

阅读量2.7k

点赞数 12

分类专栏：统计学习方法笔记文章标签：大数据

本文链接：https://blog.csdn.net/Jackson_feng/article/details/125524869

版权

统计学习方法笔记专栏收录该内容

1 篇文章 0 订阅

订阅专栏

1 引言

1957年Rosenblatt提出感知机模型，它是神经网络和支持向量机的基础。其主要适用于分类任务，训练好的感知机模型可将数据集正确地分为两类：超平面以上为正类，超平面以下为负类(后面会讲到感知机是一个超平面)。它通过利用梯度下降法最小化损失函数的思想让感知机学习到最优的状态，使得数据集的误分类点个数为0。其优点主要体现在其算法实现相对简单。

2 理论

2.1 定义

设输入特征向量为 ${\bf{x}} = {\left( {{x^{\left( 1 \right)}},\;{x^{\left( 2 \right)}},\;...,\;{x^{\left( n \right)}}} \right)^T}$ ，感知机权重为 ${\bf{\omega }} = {\left( {{\omega ^{\left( 1 \right)}},\;{\omega ^{\left( 2 \right)}},\;...,\;{\omega ^{\left( n \right)}}} \right)^T}$ ，偏置为 $b$ ，输出值为 $y \in \left\{ { - 1,\; + 1} \right\}$ ，则感知机模型定义为：

$\begin{array}{c} y\left( {\bf{x}} \right) = sign\left( {{{\bf{\omega }}^T}{\bf{x}} + b} \right)\\ = sign\left( {{\omega ^{\left( 1 \right)}}{x^{\left( 1 \right)}} + {\omega ^{\left( 2 \right)}}{x^{\left( 2 \right)}} + ... + {\omega ^{\left( n \right)}}{x^{\left( n \right)}} + b} \right) \end{array}(1)$

这是一个将 $\mathbb{R}^n$ 的输入空间转换为 $\mathbb{R}$ 的输出空间的感知机模型，其中的 $sign$ 函数定义为：

$sign\left( x \right) = \left\{ \begin{array}{l} + 1\;\;\;\;x \ge 0\\ - 1\;\;\;\;x < 0 \end{array} \right.(2)$

2.2 几何解释

设超平面 $f\left( {\bf{x}} \right) = {{\bf{\omega }}^T}{\bf{x}} + b$ ，数据集 $T = \left\{ {\left( {{{\bf{x}}_1},\;{y_1}} \right),\;\left( {{{\bf{x}}_2},\;{y_2}} \right),\;...,\;\left( {{{\bf{x}}_m},\;{y_m}} \right)} \right\}$ ，若这个超平面可将这个数据集的 $m$ 个样本点划分到超平面的两边，则这个超平面可以定义为一个感知机模型。

图1 感知机几何解释

如图1所示绿线代表超平面 $f\left( {\bf{x}} \right)$ ，数据集 $T$ 有17个样本：红色三角形代表 $y = - 1$ 类别的样本，其样本数量为8；蓝色圆点代表 $y=+1$ 类别的样本，其样本数量为9。图1的超平面 $f\left( {\bf{x}} \right)$ 将数据集 $T$ 的样本划分成了两个类别：超平面以下的样本属于-1类，超平面以上的属于+1类。

2.3 数据集的线性可分性

给定数据集 $T = \left\{ {\left( {{{\bf{x}}_1},\;{y_1}} \right),\;\left( {{{\bf{x}}_2},\;{y_2}} \right),\;...,\;\left( {{{\bf{x}}_m},\;{y_m}} \right)} \right\}$ ，若存在一个超平面 ${f^*}\left( {\bf{x}} \right)$ ：

${f^*}\left( {\bf{x}} \right) = {{\bf{\omega }}^*}^T{\bf{x}} + {b^*}(3)$

能够将数据集正确地划分出来则称这个数据集为线性可分数据集。如图1所示超平面将数据集正确划分成了+1类和-1类，则这个数据集称为线性可分数据集。

2.4 感知机的学习策略

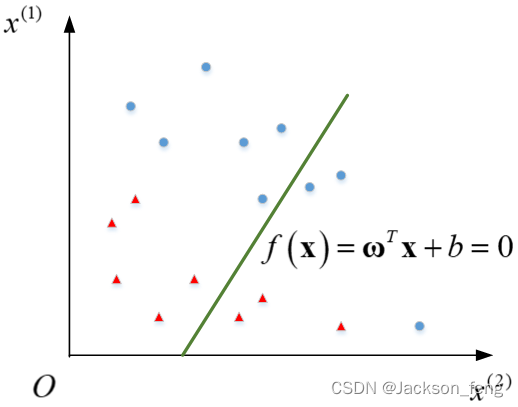
图2 误分类的感知机模型

感知机可以通过学习的方式更新参数( $\bf{\omega}$ 和 $b$ )拟合出一个能将线性可分数据集 $T$ 正确分类的超平面。假设初始随机设置超平面 $f\left( {\bf{x}} \right)$ 的参数为 ${\bf{\omega }} = {\left( {\omega _0^{\left( 1 \right)},\;\omega _0^{\left( 2 \right)},\;...,\;\omega _0^{\left( n \right)}} \right)^T}$ ， $b = {b_0}$ ，此时误分类样本点的集合为 $E = \left\{ {\left( {{{\bf{x}}_1},\;{y_1}} \right),\;\left( {{{\bf{x}}_2},\;{y_2}} \right),\;...,\;\left( {{{\bf{x}}_M},\;{y_M}} \right)} \right\}$ (如图2所示)。感知机学习的目标是让误分类样本点集合 $E$ 的长度 $M$ 极小化，则只需使得超平面 $f\left( {\bf{x}} \right)$ 往着集合 $E$ 中的样本点方向更新。若集合 $E$ 中的点到 $f\left( {\bf{x}} \right)$ 的距离和为：

$L\left( {{\bf{\omega }},\;b} \right) = \sum\limits_{i = 1}^M {\frac{{\left| {\bf{\omega}}^T{\bf{x}}_i + b \right|}}{{\left\| {\bf{\omega }} \right\|}}}(4)$

其中 ${{\bf{x}}_i} \in E$ ，则以上问题可以表示为：

$\mathop {\min }\limits_{{\bf{\omega }},\;b} \;\;L\left( {{\bf{\omega }},\;b} \right) = \sum\limits_{i = 1}^M {\frac{{\left| {\bf{\omega}}^T{\bf{x}}_i + b \right|}}{{\left\| {\bf{\omega }} \right\|}}}(5)$

由于误分类点的标签 $y_i$ 与超平面的输出 $f\left( {{{\bf{x}}_i}} \right)$ 符号相反，所以 $\left| {{{\bf{\omega }}^T}{{\bf{x}}_i} + b} \right| = - {y_i}\left( {{{\bf{\omega }}^T}{{\bf{x}}_i} + b} \right)$ 。若设 $\left\| {\bf{\omega }} \right\| = 1$ ，则公式(5)可以表示为：

$\mathop {\min }\limits_{{\bf{\omega }},\;b} \;\;L\left( {{\bf{\omega }},\;b} \right) = - \sum\limits_{i = 1}^M {{y_i}\left( {{{\bf{\omega }}^T}{{\bf{x}}_i} + b} \right)}(6)$

公式(6)是感知机学习的损失函数。

2.5 感知机的学习算法

感知机的学习算法采用梯度下降法来优化2.4节所提到的损失函数。首先对公式(6)的损失函数 $L\left( {{\bf{\omega }},\;b} \right)$ 求梯度：

$\begin{array}{l} {\nabla _{\bf{\omega }}}L\left( {{\bf{\omega }},\;b} \right) = \frac{{\partial L\left( {{\bf{\omega }},\;b} \right)}}{{\partial {\bf{\omega }}}} = - \sum\limits_{i = 1}^M {{y_i}{{\bf{x}}_i}} \\ {\nabla _b}L\left( {{\bf{\omega }},\;b} \right) = \frac{{\partial L\left( {{\bf{\omega }},\;b} \right)}}{{\partial b}} = - \sum\limits_{i = 1}^M {{y_i}} \end{array}(7)$

由梯度下降法得到参数更新公式：

$\begin{array}{l} {\bf{\omega }} \leftarrow {\bf{\omega }} + \eta {y_i}{{\bf{x}}_i}\\ b \leftarrow b + \eta {y_i} \end{array}(8)$

其中 $\eta$ 为学习率且 $\eta \in \left[ {0,\;1} \right]$ ， $\left( {{{\bf{x}}_i},\;{y_i}} \right) \in E$ 。通过调节学习率的大小可以改变整个算法的收敛速度。由以上步骤导出感知机学习算法(算法1)。

2.6 感知机的对偶学习算法

对于公式(6)的优化参数有 $\bf{\omega}$ 和 $b$ 两个变量，更新这两个变量的算法复杂度较高。为了降低算法复杂度，这里提出了一种感知机的对偶学习算法，它将原算法的优化参数 $\bf{\omega}$ 和 $b$ 改为 $\bf{\alpha}$ 和 $b$ ，下面将列出详细推导这个算法的步骤。

定义 ${{\bf{\omega }}_t}$ 和 $b_t$ 为第 $t$ 轮更新时的参数，则公式(8)的 $\bf{\omega}$ 更新步骤可以表示为：

${{\bf{\omega }}_t} = {{\bf{\omega }}_{t - 1}} + \eta {y_i}{{\bf{x}}_i}(9)$

经过多轮迭代，上式可以描述为：

$\begin{array}{c} {{\bf{\omega }}_t} = {{\bf{\omega }}_{t - 1}} + \eta {y_{{i_1}}}{{\bf{x}}_{{i_1}}}\\ = {{\bf{\omega }}_{t - 2}} + \eta {y_{{i_1}}}{{\bf{x}}_{{i_1}}} + \eta {y_{{i_2}}}{{\bf{x}}_{{i_2}}}\\ = ...\\ = {{\bf{\omega }}_0} + \eta \sum\limits_{k = 1}^t {{y_{{i_k}}}{{\bf{x}}_{{i_k}}}} \end{array}(10)$

${{\bf{x}}_{{i_k}}}$ 表示第 $i_k$ 轮的误分类点， ${y_{{i_k}}}$ 对应其标签。若设初始值 ${{\bf{\omega }}_0} = {{\bf{0}}^T}$ ， $n_i$ 表示数据集 $T$ 第 $i$ 个样本被误分类的次数，则公式(10)可以表示为：

${{\bf{\omega }}_t} = \sum\limits_{i = 1}^m {{n_i}\eta {y_i}{{\bf{x}}_i}}(11)$

设 ${\alpha _i} = {n_i}\eta$ ，则：

${\bf{\omega }} = \sum\limits_{i = 1}^m {{\alpha _i}{y_i}{{\bf{x}}_i}}(12)$

将公式(12)带入公式(1)可得感知机的对偶形式：

$y\left( {\bf{x}} \right) = sign\left( {{\left( \sum\limits_{i = 1}^m{\alpha_iy_i{\bf{x}}_i} \right)}^T \cdot {\bf{x}} + b} \right)(13)$

定义 ${\bf{\alpha }} = {\left( {{\alpha _1},\;{\alpha _2},\;...,\;{\alpha _m}} \right)^T}$ ，则公式(6)的损失函数的对偶形式可以表示为：

$\mathop {\min }\limits_{{\bf{\alpha}},\;b} \;\; L({\bf{\alpha}},b) = -\sum\limits_{i = 1}^My_i\left( {{\left( \sum\limits_{j = 1}^m{\alpha_jy_j{\bf{x}}_j} \right)}^T \cdot {\bf{x}}_i + b} \right)(14)$

参数更新可以表示为：

$\begin{array}{l} {\alpha _i} \leftarrow {\alpha _i} + \eta \\ b \leftarrow b + \eta {y_i} \end{array}(15)$

综上所述，感知机的对偶学习算法可以用算法2描述：

3例子

3.1 感知机学习算法

建立数据集 $T$ 它的正实例点为 ${{\bf{x}}_1} = {\left( {3,\;3} \right)^T}$ ， ${{\bf{x}}_2} = {\left( {4,\;3} \right)^T}$ ，负实例点为 ${{\bf{x}}_3} = {\left( {1,\;1} \right)^T}$ ，试用感知机学习算法求感知机模型 $y\left( {\bf{x}} \right) = sign\left( {{{\bf{\omega }}^T}{\bf{x}} + b} \right)$ 。(学习率 $\eta=1$ )

解：选取初始化参数 ${\bf{\omega }} = {\left( {0,\;0} \right)^T}$ ， $b = 0$

第1轮： ${\bf{\omega }} = {\left( {0,\;0} \right)^T}$ ， $b=0$

${y_1}\left( {{{\bf{\omega }}^T}{{\bf{x}}_1} + b} \right) = \left( {0,\;0} \right)\left[ \begin{array}{l} 3\\ 3 \end{array} \right] + 0 = 0 \le 0$ 更新参数：

${\bf{\omega }} \leftarrow {\bf{\omega }} + \eta {y_1}{{\bf{x}}_1} = {\left( {0,\;0} \right)^T} + {\left( {3,\;3} \right)^T} = {\left( {3,\;3} \right)^T}$

$b \leftarrow b + \eta {y_1} = 0 + 1 = 1$

第2轮： ${\bf{\omega }} = {\left( {3,\;3} \right)^T}$ ， $b=1$

${y_1}\left( {{{\bf{\omega }}^T}{{\bf{x}}_1} + b} \right) = \left( {3,\;3} \right)\left[ \begin{array}{l} 3\\ 3 \end{array} \right] + 1 = 19 > 0$

${y_2}\left( {{{\bf{\omega }}^T}{{\bf{x}}_2} + b} \right) = \left( {3,\;3} \right)\left[ \begin{array}{l} 4\\ 3 \end{array} \right] + 1 = 22 > 0$

${y_3}\left( {{{\bf{\omega }}^T}{{\bf{x}}_3} + b} \right) = - \left( {\left( {3,\;3} \right)\left[ \begin{array}{l} 1\\ 1 \end{array} \right] + 1} \right) = - 7 \le 0$ 更新参数：

${\bf{\omega }} \leftarrow {\bf{\omega }} + \eta {y_3}{{\bf{x}}_3} = {\left( {3,\;3} \right)^T} - {\left( {1,\;1} \right)^T} = {\left( {2,\;2} \right)^T}$

$b \leftarrow b + \eta {y_3} = 1 - 1 = 0$

第3轮： ${\bf{\omega }} = {\left( {2,\;2} \right)^T}$ ， $b=0$

${y_1}\left( {{{\bf{\omega }}^T}{{\bf{x}}_1} + b} \right) = \left( {2,\;2} \right)\left[ \begin{array}{l} 3\\ 3 \end{array} \right] + 0 = 12 > 0$

${y_2}\left( {{{\bf{\omega }}^T}{{\bf{x}}_2} + b} \right) = \left( {2,\;2} \right)\left[ \begin{array}{l} 4\\ 3 \end{array} \right] + 0 = 14 > 0$ ${y_3}\left( {{{\bf{\omega }}^T}{{\bf{x}}_3} + b} \right) = - \left( {\left( {2,\;2} \right)\left[ \begin{array}{l} 1\\ 1 \end{array} \right] + 0} \right) = - 4 \le 0$ 更新参数：

${\bf{\omega }} \leftarrow {\bf{\omega }} + \eta {y_3}{{\bf{x}}_3} = {\left( {2,\;2} \right)^T} - {\left( {1,\;1} \right)^T} = {\left( {1,\;1} \right)^T}$

$b \leftarrow b + \eta {y_3} = 0 - 1 = - 1$

表1 感知机算法的迭代过程

则 ${\bf{\omega }} = {\left( {1,\;1} \right)^T}$ ， $b=-3$

$\therefore y\left( {\bf{x}} \right) = sign\left( {{x^{(1)}} + {x^{(2)}} - 3} \right)$

3.2 感知机对偶形式学习算法

建立数据集 $T$ ，它的正实例点为 ${{\bf{x}}_1} = {\left( {3,\;3} \right)^T}$ ， ${{\bf{x}}_2} = {\left( {4,\;3} \right)^T}$ ，负实例点为 ${{\bf{x}}_3} = {\left( {1,\;1} \right)^T}$ ，试用感知机对偶学习算法求感知机模型 $y\left( {\bf{x}} \right) = sign\left( {{{\bf{\omega }}^T}{\bf{x}} + b} \right)$ 。(学习率 $\eta=1$ )

解：选取初始化参数 ${\bf{\alpha }} = {\left( {0,\;0,\;0} \right)^T}$ ， $b=0$

第1轮： ${\bf{\alpha }} = {\left( {0,\;0,\;0} \right)^T}$ ， $b=0$

$y_1\left( {{\left( \sum\limits_{j = 1}^m{\alpha_jy_j{\bf{x}}_j} \right)}^T \cdot {\bf{x}}_1 + b} \right) = \left( {0,0} \right)\left[ \begin{array}{l} 3\\ 3 \end{array} \right] + 0 = 0 \le 0$ 更新参数：

${\alpha _1} \leftarrow {\alpha _1} + \eta = 0 + 1 = 1$

$b \leftarrow b + \eta {y_1} = 0 + 1 = 1$

第2轮： ${\bf{\alpha }} = {\left( {1,\;0,\;0} \right)^T}$ ， $b=1$

$y_1\left( {{\left( \sum\limits_{j = 1}^m{\alpha_jy_j{\bf{x}}_j} \right)}^T \cdot {\bf{x}}_1 + b} \right)\ = \left( {3,3} \right)\left[ \begin{array}{l} 3\\ 3 \end{array} \right] + 1 = 19 > 0$

$y_2\left( {{\left( \sum\limits_{j = 1}^m{\alpha_jy_j{\bf{x}}_j} \right)}^T \cdot {\bf{x}}_2 + b} \right) = \left( {3,3} \right)\left[ \begin{array}{l} 4\\ 3 \end{array} \right] + 1 = 22 > 0$

$y_3\left( {{\left( \sum\limits_{j = 1}^m{\alpha_jy_j{\bf{x}}_j} \right)}^T \cdot {\bf{x}}_3 + b} \right)\ = - \left( {\left( {3,3} \right)\left[ \begin{array}{l} 1\\ 1 \end{array} \right] + 1} \right) = - 7 \le 0$ 更新参数：

${\alpha _3} \leftarrow {\alpha _3} + \eta = 0 + 1 = 1$

$b \leftarrow b + \eta {y_3} = 1 - 1 = 0$

第3轮： ${\bf{\alpha }} = {\left( {1,\;0,\;1} \right)^T}$ ， $b=0$

$y_1\left( {{\left( \sum\limits_{j = 1}^m{\alpha_jy_j{\bf{x}}_j} \right)}^T \cdot {\bf{x}}_1 + b} \right) = \left( {2,2} \right)\left[ \begin{array}{l} 3\\ 3 \end{array} \right] + 0 = 12 > 0$

$y_2\left( {{\left( \sum\limits_{j = 1}^m{\alpha_jy_j{\bf{x}}_j} \right)}^T \cdot {\bf{x}}_2 + b} \right) = \left( {2,2} \right)\left[ \begin{array}{l} 4\\ 3 \end{array} \right] + 0 = 14 > 0$

$y_3\left( {{\left( \sum\limits_{j = 1}^m{\alpha_jy_j{\bf{x}}_j} \right)}^T \cdot {\bf{x}}_3 + b} \right) = - \left( {\left( {2,2} \right)\left[ \begin{array}{l} 1\\ 1 \end{array} \right] + 0} \right) = - 4 \le 0$ 更新参数：

${\alpha _3} \leftarrow {\alpha _3} + \eta = 1 + 1 = 2$

$b \leftarrow b + \eta {y_3} = 0 - 1 = - 1$

表2 感知机对偶算法的迭代过程

${\bf{\omega }} = \sum\limits_{j = 1}^m {{\alpha _j}{y_j}{{\bf{x}}_j}} = 2 \cdot {\left( {3,\;3} \right)^T} - 5 \cdot {\left( {1,\;1} \right)^T} = {\left( {1,\;1} \right)^T}$

则 ${\bf{\omega }} = {\left( {1,\;1} \right)^T}$ ， $b=-3$

$\therefore y\left( {\bf{x}} \right) = sign\left( {{x^{(1)}} + {x^{(2)}} - 3} \right)$

4课后习题

4.1 (习题2.1)Minsky与Papert指出：感知机因为是线性模型，所以不能表示复杂的函数，如异或(XOR)。验证感知机为什么不能表示异或。

解：异或函数是一种非线性函数，它是一种线性不可分函数。而感知机是线性模型，所以感知机不能表示异或(如图3所示)。

图3 误分类的感知机模型

4.2 (习题2.2)模仿例题2.1，构建从训练数据集求解感知机模型的例子。

解：设正样本点为： ${{\bf{x}}_1} = {\left( {1,\;1,\;2} \right)^T}$ ， ${{\bf{x}}_2} = {\left( {2,\;2,\;1} \right)^T}$ ；负样本点为： ${{\bf{x}}_3} = {\left( {4,\;3,\;3} \right)^T}$ ，则：

表3 习题2.2求解过程

则 ${\bf{\omega }} = {\left( { - 8,\;1,\;5} \right)^T}$ ， $b=11$

$\therefore y\left( {\bf{x}} \right) = sign\left( { - 8{x^{(1)}} + {x^{(2)}} + 5{x^{(3)}} + 11} \right)$

4.3 (习题2.3)证明以下定理：样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集所构成的凸壳不相交。

证：设正样本点集合为： ${S^ + } = {\left( {s_1^ + ,\;s_2^ + ,\;...,\;s_N^ + } \right)^T}$ ，负样本点集合为 ${S^ - } = {\left( {s_1^ - ,\;s_2^ - ,\;...,\;s_M^ - } \right)^T}$ ，则它们的凸壳分别为：

$conv\left( {{S^ + }} \right) = \left\{ {\left. {{s^ + } = \sum\limits_{i = 1}^N {{\lambda _i}s_i^ + } } \right|\sum\limits_{i = 1}^N {{\lambda _i}} = 1,\;\;{\lambda _i} \ge 0,\;\;i = 1,\;...,\;N} \right\}$

$conv\left( {{S^ - }} \right) = \left\{ {\left. {{s^ - } = \sum\limits_{i = 1}^M {{v_i}s_i^ - } } \right|\sum\limits_{i = 1}^M {{v_i}} = 1,\;\;{v_i} \ge 0,\;\;i = 1,\;...,\;M} \right\}$

① 充分性；正、负样本点集凸壳不相交 $\Rightarrow$ 样本集线性可分：

因为 $conv\left( {{S^ + }} \right) \cap conv\left( {{S^ - }} \right) = \emptyset$ ，则：

$\forall \;\;{{\bf{x}}_1} \in conv\left( {{S^ + }} \right),\;\;{{\bf{x}}_2} \in conv\left( {{S^ - }} \right)\;\;s.t.\;\;{{\bf{x}}_1} \ne {{\bf{x}}_2}$

且 $\exists \;\;f\left( {\bf{x}} \right) = sign\left( {{{\bf{\omega }}^T}{\bf{x}} + b} \right)$ 使得 $conv\left( {{S^ + }} \right)$ 与 $conv\left( {{S^ - }} \right)$ 线性可分，则：

$f\left( {{{\bf{x}}_1}} \right) = sign\left( {{{\bf{\omega }}^T}{{\bf{x}}_1} + b} \right) = 1,\;\;{{\bf{\omega }}^T}{{\bf{x}}_1} > - b$

$f\left( {{{\bf{x}}_2}} \right) = sign\left( {{{\bf{\omega }}^T}{{\bf{x}}_2} + b} \right) = - 1,\;\;{{\bf{\omega }}^T}{{\bf{x}}_2} < - b$

若：

$\exists \;\;{{\bf{x}}_1} \in conv\left( {{S^ + }} \right),\;\;{{\bf{x}}_2} \in conv\left( {{S^ - }} \right)\;\;s.t.\;\;{{\bf{x}}_1} = {{\bf{x}}_2}$

且 $\exists \;\;f\left( {\bf{x}} \right) = sign\left( {{{\bf{\omega }}^T}{\bf{x}} + b} \right)$ 使得 $conv\left( {{S^ + }} \right)$ 与 $conv\left( {{S^ - }} \right)$ 线性可分，则：

$f\left( {{{\bf{x}}_1}} \right) = sign\left( {{{\bf{\omega }}^T}{{\bf{x}}_1} + b} \right) = 1,\;\;{{\bf{\omega }}^T}{{\bf{x}}_1} > - b$

$f\left( {{{\bf{x}}_2}} \right) = sign\left( {{{\bf{\omega }}^T}{{\bf{x}}_2} + b} \right) = - 1,\;\;{{\bf{\omega }}^T}{{\bf{x}}_2} < - b$

所以 ${{\bf{x}}_1} \ne {{\bf{x}}_2}$ ，与原问题矛盾。

② 必要性：样本集线性可分 $\Rightarrow$ 正、负样本点集凸壳不相交

当：

$\forall \;\;{{\bf{x}}_1} \in conv\left( {{S^ + }} \right),\;\;{{\bf{x}}_2} \in conv\left( {{S^ - }} \right)$

且 $\exists \;\;f\left( {\bf{x}} \right) = sign\left( {{{\bf{\omega }}^T}{\bf{x}} + b} \right)$ 使得 $conv\left( {{S^ + }} \right)$ 与 $conv\left( {{S^ - }} \right)$ 线性可分，所以：

$f\left( {{{\bf{x}}_1}} \right) = sign\left( {{{\bf{\omega }}^T}{{\bf{x}}_1} + b} \right) = 1,\;\;{{\bf{\omega }}^T}{{\bf{x}}_1} > - b$

$f\left( {{{\bf{x}}_2}} \right) = sign\left( {{{\bf{\omega }}^T}{{\bf{x}}_2} + b} \right) = - 1,\;\;{{\bf{\omega }}^T}{{\bf{x}}_2} < - b$

则 ${{\bf{x}}_1} \ne {{\bf{x}}_2} \Rightarrow conv\left( {{S^ + }} \right) \cap conv\left( {{S^ - }} \right) = \emptyset$

5参考文献

[1] 李航. 统计学习方法[M]. 清华大学出版社, 2012.

[2] Rosenblatt, F. The perceptron: a probabilistic model for information storage and organization in the brain.[J]. Psychological Review, 1958, 65:386-408.

代码实现

A 算法2.1

import numpy as np
# 感知机学习算法
class Perceptron:
    def __init__(self, X, y):
        self.X=np.array(X)
        self.y=np.array(y)
        self.w=np.zeros(self.X.shape[1])
        self.b=0

    def train(self,ita):
        k,epoch=0,0
        while k<self.y.shape[0]:
            k=0
            for _X,_y in zip(self.X,self.y):
                if _y*(np.dot(self.w,_X.T)+self.b)<=0:
                    self.w=self.w+ita*_y*_X
                    self.b=self.b+ita*_y
                    break
                else:
                    k+=1
            print(f"epoch={epoch}:\tw={self.w}\tb={self.b}")
            epoch+=1



if __name__=="__main__":
    X=[[3,3],[4,3],[1,1]]
    y=[1,1,-1]

    print("\n感知机学习算法：\n")
    perc=Perceptron(X,y)
    perc.train(ita=1)

B 算法2.2

# 感知机对偶形式学习算法
class DualPerceptron:
    def __init__(self, X, y):
        self.X=np.array(X)
        self.y=np.array(y)
        self.alpha=np.zeros(self.X.shape[0])
        self.b=0

    def train(self,ita):
        k,epoch=0,0
        while k<self.y.shape[0]:
            k=0
            for i,data in enumerate(zip(self.X,self.y),0):
                _X,_y=data
                temp=np.zeros(self.X.shape[1])
                for alphaj,xj,yj in zip(self.alpha,self.X,self.y):
                    temp=temp+alphaj*xj*yj
                if _y*(np.dot(temp,_X.T)+self.b)<=0:
                    self.alpha[i]=self.alpha[i]+1
                    self.b=self.b+ita*_y
                    break
                else:
                    k+=1
            print(f"epoch={epoch}:\talpha={self.alpha}\tb={self.b}")
            epoch+=1
        self.w=np.zeros(self.X.shape[1])
        for alphaj, xj, yj in zip(self.alpha, self.X, self.y):
            self.w = self.w + alphaj * xj * yj

if __name__=="__main__":
    X=[[3,3],[4,3],[1,1]]
    y=[1,1,-1]


    print("\n感知机对偶形式学习算法：\n")
    dual_perc=DualPerceptron(X, y)
    dual_perc.train(ita=1)

*本文仅代表作者自己的观点，欢迎大家批评指正