环形染色问题

Jaydenyu2012

已于 2023-10-01 09:00:54 修改

阅读量7.9k

点赞数 4

分类专栏：排列组合

于 2022-07-23 10:58:48 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/Jaydenyu2012/article/details/125934388

版权

环形染色排列组合通项公式等比数列数学模型

关键词由CSDN通过智能技术生成

排列组合专栏收录该内容

1 篇文章

订阅专栏

本文讲述了环形染色问题，属于排列组合

如图所示，一个圆环被分成 m 块，用 n 种不同颜色给每一块染色，要求相邻两块的颜色不相同。此类问题称之为环形染色问题。

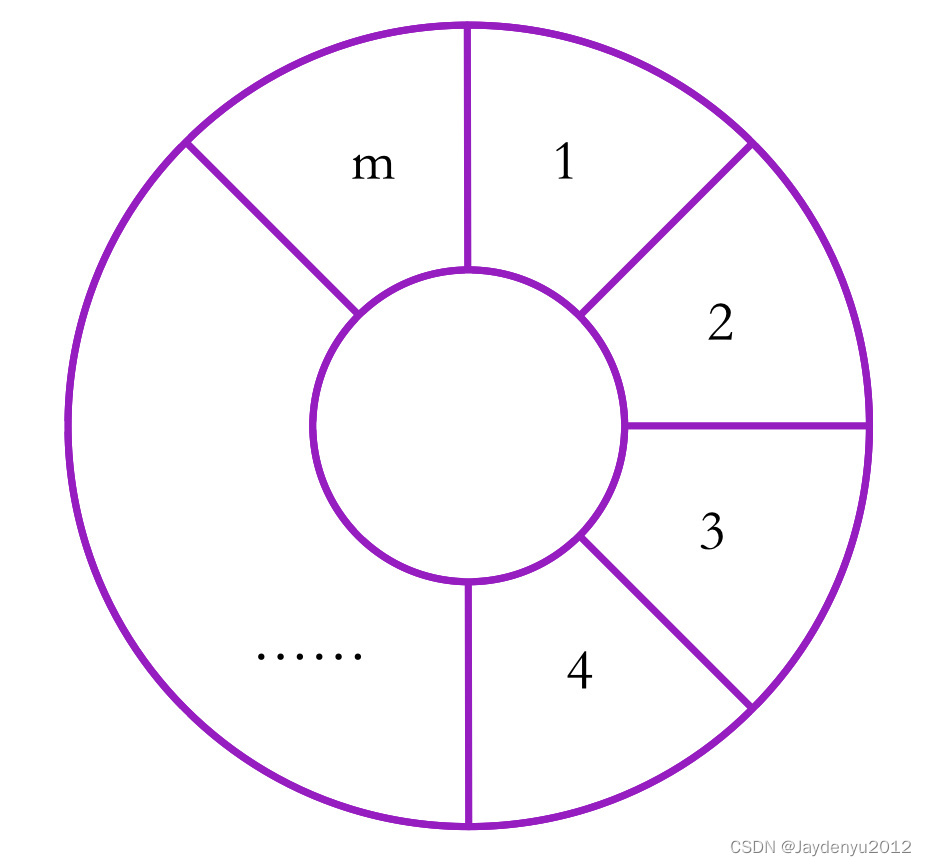
首先，先用分类讨论来讲一下 $n=4,m=4$ 的情况

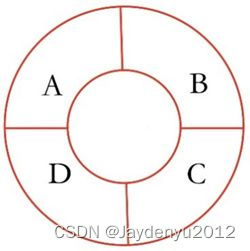
首先，加编号

先考虑A——>4（n）种

B——>3（n-1）种

①：A=C

        C——>1（A）种

        D——>3 【n(4) - A/C（1）=3】种

         $\\ Total_{A=C}=A\times B\times C\times D=4\times 3 \times 1\times3=36$

②：A≠C

C——>2【n(4) - A(1) - B(1) = 2】种

D——>2【n(4) - A(1) - C(1) = 2】种

         $Total_{A \neq C}=A\times B\times C\times D=4\times 3 \times 2\times2=48$

$Total=Total_{A=C}+Total_{A\ne C}=36+48=84$

有没有通项公式，那肯定有！

令一数列 $a_i$ ：m=i 的情况数

Step 1:把环变成条

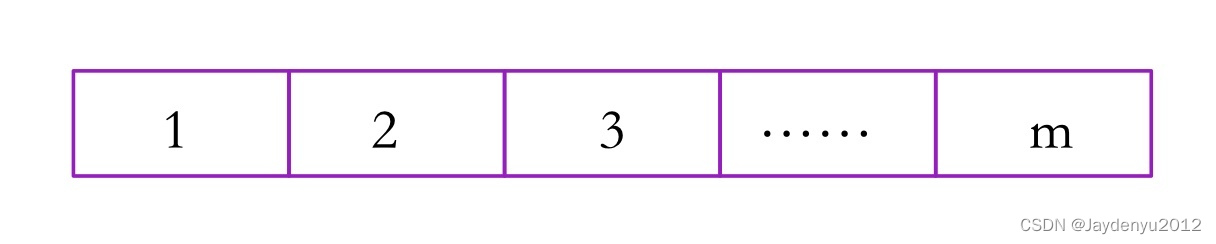
情况数记作 $T_i=i\cdot (i-1)^{m-1}$ ,为什么不用多说，乘法原理即可(mj是第 j 个点的情况数) $\{_{m_j=i\ \ \ \ \ \ \ \ \ \ \ i=1} ^{m_j=(i-1)\ \ \ \ \ \ other}$

那 $a_i$ 与 $T_i$ 有啥区别？

对， $\\a_i : m_1 \ne m_n\\ T_i:m_1 \ne m_n \ or \ m_1=m_n$

那 $a_1=a_n\\So \ a_1\ne a_{n-1}$

所以剩余情况就是 $a_{i-1}$ （其他也都满足要求）

可得一个式子： $a_i+a_{i-1}=T_i=n\cdot(n-1)^{i-1}$ 记作①式

结束了吗，NO!

Step 2:

右式换个模样： $n\cdot(n-1)^{i-1}\\=(n-1+1)\cdot(n-1)^{i-1}\\=(n-1)\cdot(n-1)^{i-1}+(n-1)^{i-1}\\=(n-1)^i+(n-1)^{i-1}$

移项可得， $a_i-(n-1)^i=(n-1)^{i-1}-a_{i-1}$ 记作②式

令一数列 b, $b_i=a_i-(n-1)^m$ 记作③式

那 $\frac{b_i}{b_{i-1}}=\frac{a_i-(n-1)^i}{a_{i-1}-(n-1)^{i-1}}$ 记作④式

①式移项可得: $a_{i-1}=n\cdot(n-1)^{i-1}-a_i$

把 $a_{i-1}$ 的值带入④式

$\\ \frac{b_i}{b_{i-1}}=\frac{a_i-(n-1)^i}{n\cdot(n-1)^{i-1}-a_i-(n-1)^{i-1}} \\ \\ = \ \ \ \ \ \ \frac{a_i-(n-1)^i}{(n-1)^i-a_i} = -1$

所以 b 为等比数列

已知 $a_2=n\cdot (n-1)$

那 $b_2=a_2-(n-1)^2=n\cdot (n-1)-(n-1)^2=n-1$

等比数列，那 $b_n=(-1)^{n-2}\cdot b_2$

把 $b_2=n-1$ 带入此式， $b_n=(-1)^n\cdot(n-1)$

③式移项： $a_i=b_i+(n-1)^i$

把 $b_i$ 的值带入此式

$a_i=(n-1)^m+(-1)^m\cdot (n-1)$

验：当n=4,m=4, $a_4=(4-1)^4+(-1)^4\cdot(4-1)=3^4+3=84$

中心区域染色

圆环有m块区域，再加上中心区域共有m+1块区域；有n+1种颜色

由于中心区域与外环所有区域均相邻，则先涂中心区域，有n+1种涂色方法；

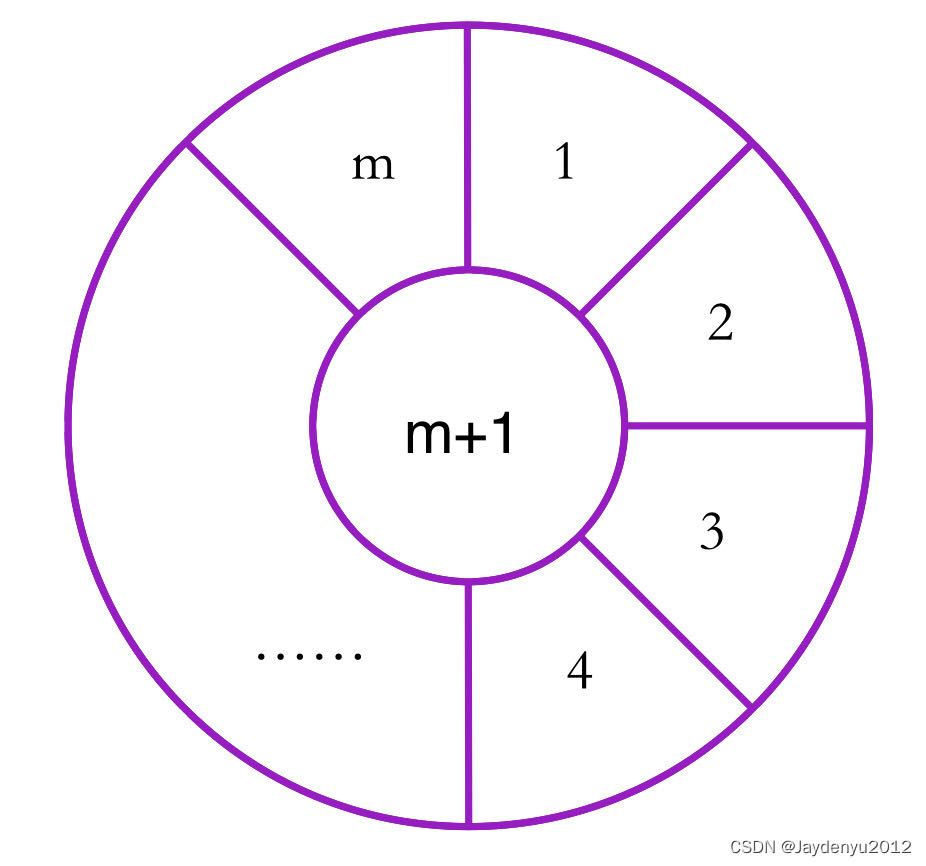
这个优先考虑(m+1),因为它影响了1~m里的所有块（1~m都不能和m+1一样）,其余就是 $a_m$

所以答案是 $(n+1)\cdot a_m=(n-1)\cdot [(n-1)^m+(-1)^m\cdot (n-1)]$

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。