分治算法--棋盘覆盖问题+逆序对（归并排序法）

噜噜啦啦~

已于 2025-05-13 17:35:04 修改

阅读量351

点赞数 7

文章标签：算法

于 2025-05-13 17:34:16 首次发布

本文链接：https://blog.csdn.net/Jdhhsuhs/article/details/147927261

版权

1.棋盘覆盖问题

1.1题目描述

1.2解题思路

⚠️建议先观看基讲解视频

步骤：

分解棋盘：将当前棋盘均分为 4 个 \(2^{k-1} \times 2^{k-1}\) 的子棋盘。
确定特殊方格位置：判断特殊方格位于哪个子棋盘中。
处理子棋盘：
- 含特殊方格的子棋盘：直接递归处理。
- 不含特殊方格的子棋盘：在交界处放置一个 L 型骨牌，使其覆盖三个子棋盘的各一个角落，将这些角落作为新的特殊方格递归处理。
递归终止：当棋盘大小为 \(1 \times 1\) 时停止。

⚠️疑难点解释--> 为什么if (dr <tr + s && dc < tc + s) 可以判断特殊方格位于左上角？

答：参数含义

tr, tc：当前棋盘左上角的行号和列号（递归过程中动态变化）。
dr, dc：特殊方格的行号和列号（全局固定）。
s：当前棋盘分割后的子棋盘大小（即 size/2）。
tr + s 和 tc + s：当前棋盘水平和垂直方向的中间线位置。

条件判断逻辑

dr < tr + s && dc < tc + s 的含义是：

dr < tr + s：特殊方格的行号位于当前棋盘上半部分。
dc < tc + s：特殊方格的列号位于当前棋盘左半部分。

1.3代码展示

#include <iostream>
using namespace std;

// 全局变量表示骨牌编号
int tile = 1;

// 棋盘覆盖函数
// tr, tc: 棋盘左上角的行号和列号
// dr, dc: 特殊方格的行号和列号
// size: 当前棋盘的大小(2^k)
void chessBoard(int tr, int tc, int dr, int dc, int size) {
    if (size == 1) return;  // 递归终止条件
    int t = tile++;         // 骨牌编号
    int s = size / 2;       // 分割棋盘
    
    // 覆盖左上角子棋盘
    if (dr < tr + s && dc < tc + s)
        // 特殊方格在此棋盘中
        chessBoard(tr, tc, dr, dc, s);
    else {
        // 此棋盘中无特殊方格，用一个骨牌覆盖右下角
        board[tr + s - 1][tc + s - 1] = t;
        chessBoard(tr, tc, tr + s - 1, tc + s - 1, s);
    }
    
    // 覆盖右上角子棋盘
    if (dr < tr + s && dc >= tc + s)
        // 特殊方格在此棋盘中
        chessBoard(tr, tc + s, dr, dc, s);
    else {
        // 此棋盘中无特殊方格，用一个骨牌覆盖左下角
        board[tr + s - 1][tc + s] = t;
        chessBoard(tr, tc + s, tr + s - 1, tc + s, s);
    }
    
    // 覆盖左下角子棋盘
    if (dr >= tr + s && dc < tc + s)
        // 特殊方格在此棋盘中
        chessBoard(tr + s, tc, dr, dc, s);
    else {
        // 此棋盘中无特殊方格，用一个骨牌覆盖右上角
        board[tr + s][tc + s - 1] = t;
        chessBoard(tr + s, tc, tr + s, tc + s - 1, s);
    }
    
    // 覆盖右下角子棋盘
    if (dr >= tr + s && dc >= tc + s)
        // 特殊方格在此棋盘中
        chessBoard(tr + s, tc + s, dr, dc, s);
    else {
        // 此棋盘中无特殊方格，用一个骨牌覆盖左上角
        board[tr + s][tc + s] = t;
        chessBoard(tr + s, tc + s, tr + s, tc + s, s);
    }
}

int main() {
    int k = 2;  // 棋盘大小为2^k × 2^k
    int size = 1 << k;  // 等价于2^k
    
    // 动态分配棋盘数组
    int **board = new int*[size];
    for (int i = 0; i < size; i++) {
        board[i] = new int[size];
        for (int j = 0; j < size; j++) {
            board[i][j] = 0;  // 初始化棋盘
        }
    }
    
    // 设置特殊方格位置(0-based)
    int dr = 0, dc = 1;
    board[dr][dc] = -1;  // 特殊方格标记为-1
    
    // 执行棋盘覆盖
    chessBoard(0, 0, dr, dc, size);
    
    // 输出结果
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            cout << board[i][j] << "\t";
        }
        cout << endl;
    }
    
    // 释放内存
    for (int i = 0; i < size; i++) {
        delete[] board[i];
    }
    delete[] board;
    
    return 0;
}

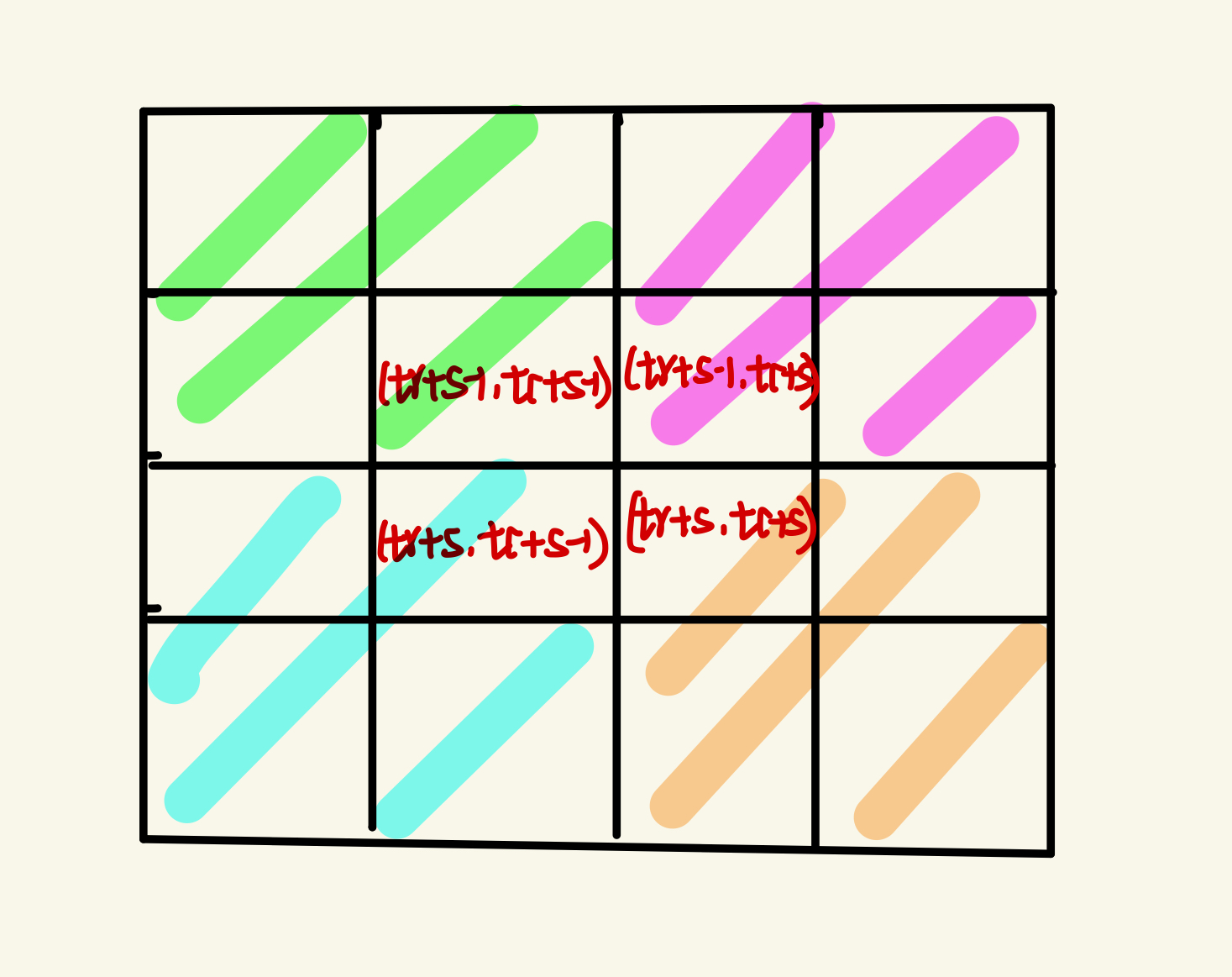
假定size=4，则第一次递归的图为：

2.逆序对

2.1题目描述

给定一个数组 arr，如果存在索引对 (i, j) 满足 i < j 且 arr[i] > arr[j]，则称 (i, j) 为一个逆序对。请计算数组中所有逆序对的总数。

2.2解题思路

⚠️先复习一下归并排序：

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

📍核心原理📍

归并排序统计逆序对的原理

逆序对定义为：对于数组中的元素对 (i, j)，若 i < j 且 arr[i] > arr[j]，则称为一个逆序对。

在归并排序的合并阶段，当我们需要将两个有序子数组 left[low..mid] 和 right[mid+1..high] 合并时：

如果选择了右子数组的元素 right[j]，说明左子数组中剩余的所有元素都比 right[j] 大（因为左子数组已排序）。
这些剩余元素的数量即为当前产生的逆序对数量（因为它们的索引都小于 j，但值都大于 right[j]）。

例如：
左子数组：[5, 7, 9]  右子数组：[2, 4, 6]
          ↑                     ↑
          i                     j

当 j 指向 2 时，i 指向 5。由于 5 > 2，说明左子数组中 [5, 7, 9] 都与 2 构成逆序对，共 3 个。

2.3代码展示

#include <iostream>
#include <vector>
using namespace std;

// 归并排序并统计逆序对
int mergeSort(vector<int>& arr, int left, int right) {
    if (left >= right) return 0;  // 递归终止条件
    
    int mid = left + (right - left) / 2;
    // 分治：分别统计左右子数组的逆序对
    int inv_count = mergeSort(arr, left, mid) + mergeSort(arr, mid + 1, right);
    
    // 合并两个有序子数组并统计跨越左右的逆序对
    vector<int> temp(right - left + 1);
    int i = left, j = mid + 1, k = 0;
    
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
            inv_count += mid - i + 1;  // ⚠️⚠️⚠️关键：左子数组剩余元素均与arr[j]构成逆序对
        }
    }
    
    // 处理剩余元素
    while (i <= mid) temp[k++] = arr[i++];
    while (j <= right) temp[k++] = arr[j++];
    
    // 复制回原数组
    for (i = left, k = 0; i <= right; i++, k++) {
        arr[i] = temp[k];
    }
    
    return inv_count;
}

int main() {
    vector<int> arr = {5, 3, 2, 4, 1};
    int inv_count = mergeSort(arr, 0, arr.size() - 1);
    
    cout << "逆序对数量: " << inv_count << endl;  // 输出：7
    return 0;
}