一、The Shannon-Nyquist Sampling Theorem
问题:原始数据是连续函数,是否能用有限个采样百分之百重现原始数据?
香农回答了这个问题:如果原始数据中最大频率为f,如果采样频率为2f,即每隔1/(2f)秒取一次样,则可完全恢复原始数据。
陆吾生教授2010年的视频中给出了非常直观的解释:
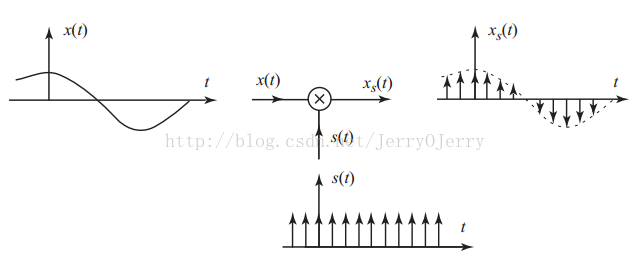
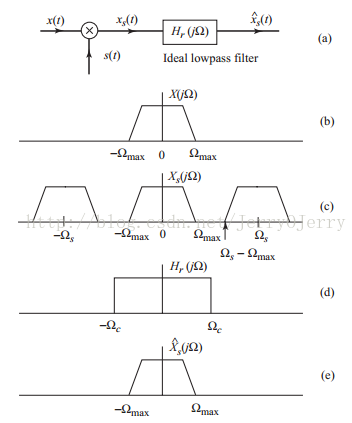
图a是采样和恢复过程,图b表示原始函数的傅里叶变换得到的频域分布,图c表示取样后的频域分布,可以看到是原始频域分布复制粘贴,且按采样频率位移,因为频率分布不能重叠,否则信息就会丢失,这个用公式表示就是下图的关系,所以可以很容易得到采样频率和原始频率的关系,图d是低通滤波器,图e是低通部分,即原始数据的频率分布。
最终的恢复公式就是,可以看成是采样后的信号与sinc函数卷积的结果:





 本文探讨了压缩感知的理论基础,包括Shannon-Nyquist采样定理,以及稀疏信号的表示和压缩。介绍了小波变换在稀疏信号处理中的作用,并讨论了如何寻找最稀疏的解决方案。文章还深入浅出地阐述了压缩采样的概念,提出了直接在信息密度较高的空间采样的可能性,最后提到了用于信号恢复的最优化问题和相关工具。
本文探讨了压缩感知的理论基础,包括Shannon-Nyquist采样定理,以及稀疏信号的表示和压缩。介绍了小波变换在稀疏信号处理中的作用,并讨论了如何寻找最稀疏的解决方案。文章还深入浅出地阐述了压缩采样的概念,提出了直接在信息密度较高的空间采样的可能性,最后提到了用于信号恢复的最优化问题和相关工具。
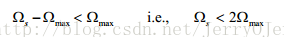
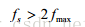
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2181
2181

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








